12.2 Demodulazione di ampiezza
Il segnale informativo m(t) può essere recuperato a partire da quello modulato x(t) mediante il processo di demodulazione, che nel caso am può avvenire mediante diverse tecniche, denominate omodina, di inviluppo, in fase e quadratura, eterodina; ognuna di esse ha il suo campo di applicazione, assieme a pregi e difetti.
12.2.1 Demodulazione coerente o omodina
Si tratta del circuito già noto (vedi §
11.2.4) di estrazione della componente in fase
xc(t) mediante moltiplicazione o
mixing di
x(t) per una portante di demodulazione
cosω0t,
e di rimozione delle componenti a frequenza
2f0 mediante un filtro passa-basso, come mostrato in figura. La portante generata localmente deve avere la stessa fase e la stessa frequenza della portante ricevuta, condizione indicata anche con il nome di demodulazione
omodina, sincrona, coerente, a
conversione diretta, o zero-
if. Il metodo è applicabile a tutti i tipi di modulazione di ampiezza, in quanto per tutti la componente in fase è direttamente legata al messaggio
m(t); nella pratica, nei casi di
bld-pi ed in quelli ad esso riconducibili, può essere invece preferibile adottare il demodulatore di inviluppo (§
12.2.5).
12.2.2 Sincronizzazione di portante
Individua il compito di generare presso il demodulatore una
copia della portante quanto più possibile
coerente con la fase di quella ricevuta. Descriviamo due dei metodi utilizzati a questo scopo, mentre un terzo attuabile con tecniche totalmente digitali è descritto al §
12.4.3.
12.2.2.1 Metodo della quadratura
Anche se nel segnale ricevuto non vi è traccia della portante, come per
bld-ps, la portante di demodulazione può essere comunque ottenuta mediante lo schema simbolico
rappresentato in figura, che come prima cosa eleva al quadrato il segnale modulato ricevuto
x(t) = m(t)cos(ω0t + φ), producendo
12 m2(t) [1 + cos(2ω0t + 2φ)]
Il termine di banda base
12m2(t) viene quindi rimosso dal filtro passa alto, mentre il termine
cos(2ω0t + 2φ) è convertito in un’onda quadra a frequenza
2f0 mediante il dispositivo non lineare
squadratore, che produce in uscita la funzione
segno di ciò che si presenta in ingresso. A sua volta l’onda quadra attraversa un divisore di frequenza, ottenendo così una nuova onda quadra, ma a frequenza
f0; come noto (§
2.5.2) l’onda quadra contiene anche tutte le armoniche dispari, che sono rimosse dal filtro passa basso di uscita,
ottenendo in definitiva la portante desiderata.
Qualora il divisore sia implementato mediante un multivibratore bistabile che commuta sul fronte di salita dell’ingresso, il metodo è affetto da una ambiguità di segno, che corrisponde ad un eventuale errore di fase pari a π, come mostrato in figura.
12.2.2.2 Phase Locked Loop o PLL
Una seconda tecnica (nota come
circuito ad aggancio di fase) adotta invece un approccio a
controreazione, e si basa sull’utilizzo di un dispositivo chiamato
oscillatore controllato in tensione (
voltage controlled oscillator o
vco) il quale genera una sinusoide
y(t) = sin (ω0t + 2πkf ⌠⌡t−∞ε(τ)dτ)
la cui fase varia nel tempo in proporzione all’integrale del segnale di ingresso
ε(τ).
Lo schema a lato illustra come il ruolo del vco sia quello di generare una portante sfasata di
π⁄2 rispetto a quella del segnale
x(t) in arrivo, mentre a quest’ultimo è richiesto di contenere almeno
un residuo di portante. In uscita dal
vco è pertanto presente il segnale
y(t) = sin(ω0t + ^θ(t)) in cui
rappresenta la
stima della fase
θ(t) del segnale in ingresso, valutata all’istante
t. Eseguendo ora il prodotto tra
y(t) ed il segnale ricevuto
x(t) = cos(ω0t + θ(t)) si ottiene
12 sin[2ω0t + θ(t) + ^θ(t)] + 12 sin[θ(t) − ^θ(t)]
il cui primo termine è centrato a frequenza doppia (
2ω0) e viene eliminato dal filtro passa basso (detto anche
filtro di loop), alla uscita del quale troviamo dunque
ε(t) = 12 sin[θ(t) − ^θ(t)] = 12 sin(Δθ(t))
dove
Δθ(t) = θ(t) − ^θ(t) rappresenta l’errore di fase che desideriamo annullare, ed
ε(t) è la grandezza in ingresso al
vco.
Pensiamo ora al caso in cui la
θ(t) presente nel segnale di ingresso sia
costante: nel momento in cui
Δθ = 0, si ottiene che anche
ε = 0, ed il
vco non altera la fase (esatta) della portante generata. Se invece
Δθ ≷ 0 (e
|Δθ| < π), allora
ε ≷ 0, e dunque
(vedi figura a lato) il
vco è portato ad aumentare (diminuire) la fase della propria portante, riducendo di conseguenza l’errore di fase. Nel caso in cui, infine, la fase
θ(t) del segnale in arrivo vari nel tempo, allora il
pll insegue tali variazioni tanto più da vicino, quanto più è elevato il coefficiente di proporzionalità
kf tra
^θ(t) e l’integrale di
ε(t) che compare nella
(14.46).
Al §
12.4.3 viene illustrato come utilizzare il
pll allo scopo di generare una portante
stabile di modulazione a frequenza qualsiasi, a partire da un oscillatore al quarzo.
12.2.3 Errori di fase e di frequenza
Cosa accade se la sincronizzazione di portante non è
perfetta? Qualora tra la portante del demodulatore (§
12.2.1) e quella del segnale in arrivo
x(t) siano presenti errori di fase
θ e/o di frequenza
Δf, ovvero risulti
x(t) = cos(2π(fo + Δf)t + θ), il risultato della demodulazione (non più coerente) risulta pari a:
y(t) = xc(t) cosω0t cos[(ωo + Δω)t + θ] = 12 xc(t) [cos(Δωt + θ) + cos((2ω0 + Δω)t + θ)]
Mentre il termine a frequenza (circa) doppia viene eliminato come di consueto dall’apposito filtro, sul segnale demodulato
y(t) si manifestano ora le seguenti distorsioni:
- in assenza di errori di frequenza (Δω = 0) si ottiene y(t) = 12 xc(t) cosθ ≤ 12 xc(t) cioè una attenuazione, che può annullare y(t) se θ = ± π2, mentre per θ = π si ottiene una inversione di segno di xc(t);
- qualora Δω ≠ 0 si ottiene y(t) = 12 xc(t) cos(Δωt) e dunque il segnale demodulato, oltre ad invertire periodicamente polarità, presenta una notevole oscillazione di ampiezza che, ad esempio, nel caso di segnale audio può rendere il risultato inintelligibile già con Δf pari a pochi Hertz.
12.2.3.1 Demodulazione I e Q in presenza di errore di fase
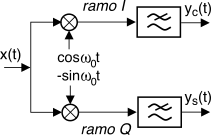
Poniamoci ora nel caso in cui nel segnale modulato siano presenti entrambe le c.a. di b.f., ovvero
x(t) = xc(t)cosω0t − xs(t)sinω0t, e si desideri demodularle entrambe.
Si ricorre allora al demodulatore
in fase e quadratura (§
11.2.4), che prevede due rami (detti anche
i e
q) con portanti di demodulazione, appunto, in quadratura.
Applicando i risultati del §
11.2.4, e con riferimento alla notazione adottata nella figura che segue, in condizioni di
coerenza si ottiene
yc(t) = 12xc(t) e
ys(t) = 12xs(t). Se viceversa il segnale ricevuto presenta una fase incognita
θ, e dunque
x(t) = xc(t)cos(ω0t + θ) − xs(t)sin(ω0t + θ)
si ottiene invece
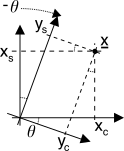
Ovviamente, per
θ = 0 le
(14.47) si riducono al caso noto, mentre
curiosamente per uno sfasamento
θ = π2 le due c.a. di b.f. (a parte un segno) si invertono di ruolo. Un ragionamento più approfondito è fornito a pag.
1, e dimostra che
θ rappresenta l’angolo di cui ruota il piano dell’inviluppo complesso tra
x(t) e
y(t). Ad ogni modo il sistema
(14.47) è perfettamente invertibile, qualora
θ sia noto.
12.2.4 Demodulazione incoerente
Si tratta di uno schema utile nella
fase di ricerca della regione di frequenza in cui è presente un segnale, ovvero quando si desidera verificare la presenza
o meno di un segnale ad una determinata frequenza. In tale schema la coerenza di fase tra la portante ricevuta e quella di demodulazione viene deliberatamente
trascurata, adottando una architettura che utilizza anche il ramo
in quadratura.
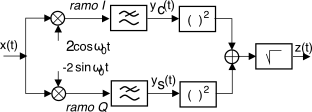
Se consideriamo un segnale
am-bld-ps ricevuto in presenza di una fase
θ incognita rispetto alla portante del ramo I del demodulatore, ovvero
x(t) = m(t) cos(ω0t + θ), il relativo inviluppo complesso rispetto ad
f0 (e
θ = 0) risulta pari a
x(t) = m(t) e jθ = m(t) cosθ + jm(t) sinθ
le cui parti reale ed immaginaria corrispondono all’uscita dei filtri passa-basso posti sui rami del demodulatore
i-q mostrato in figura, ossia
yc(t) = m(t)cosθ e
ys(t) = m(t)sinθ, come si ottiene (a parte un fattore
1⁄2) dalle
(14.47) avendo posto
xc(t) = m(t) e
xs(t) = 0. Dunque il segnale
z(t) di uscita corrisponde a
z(t) = √y2c(t) + y2s(t) = |m(t)|√cos2θ + sin2θ = |m(t)|
Pertanto, nonostante l’ignoranza della fase
θ, siamo ancora in grado di individuare la
presenza di un segnale modulante. L’operazione di modulo impedisce l’uso dello schema per demodulare generici segnali
bld-ps, mentre il caso
pi sarebbe perfettamente demodulabile, ma per quello è più che sufficiente il demodulatore
di inviluppo discusso al § seguente. Infine, al §
14.4.2 si illustra come usare il demodulatore incoerente per decidere per la presenza o meno di una sinusoide a cui è sovrapposto un rumore gaussiano, e viene valutata la relativa probabilità di errore.
12.2.5 Demodulatore di inviluppo per AM-BLD-PI
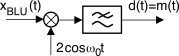
Si tratta del semplice circuito
non lineare riportato in figura. Durante i periodi in
cui il segnale in ingresso
x(t) è positivo rispetto alla tensione
d(t) accumulata dal condensatore, quest’ultimo si carica, inseguendo l’andamento dell’ingresso. Quando diviene
x(t) < d(t), il condensatore si scarica sulla resistenza con una costante di tempo (pag.
1)
τ = RC, abbastanza grande rispetto al periodo della portante
1f0, e tale da permettere la ricostruzione dell’andamento di
xc(t). Le oscillazioni a frequenza
f0 (e sue armoniche) possono quindi essere rimosse da un successivo filtro passa-basso, mentre la costante
ap è rimossa mediante un passa alto. D’altra parte, il valore di
τ deve essere scelto né troppo piccolo né troppo grande, per evitare una eccessiva
seghettatura, ed al contempo riuscire ad inseguire anche le variazioni più rapide del messaggio.
La semplicità del circuito è tale da farlo usare nel maggior numero di casi possibili, anche se il suo uso prevalente è per la demodulazione di segnali a
portante intera. D’altra parte, la contemporanea presenza di altri segnali modulati con portante diversa da quella del segnale desiderato rendono obbligatoria l’adozione di ulteriori provvedimenti, come discusso nel §
12.2.7 relativo alla demodulazione
eterodina.
12.2.6 Demodulazione per segnali a banda laterale unica e ridotta
Nel caso di segnali
blu (§ 12.1.2)
xBLU(t) = m(t) cosω0t − ^m(t) sinω0t
il segnale modulante
m(t) può essere riottenuto a partire da
x(t) utilizzando il demodulatore omodina mostrato in figura, dato che la componente in fase
xc(t) dell’inviluppo complesso corrisponde proprio pari ad
m(t). Occorre però prestare attenzione ad eventuali errori di frequenza e di fase (
Δf e
θ) della portante di demodulazione perché, essendo presenti entrambe le componenti
xc(t) ed
xs(t), come mostrato al §
12.2.3.1 in uscita dal demodulatore si ottiene (nel caso di banda laterale superiore):
d(t) = m(t) cos(Δωt + θ) − ^m(t) sin(Δωt + θ)
Pertanto la modulazione
blu è più sensibile di quella
bld agli errori della portante di demodulazione, dato che anche un semplice errore di fase
θ produce non solo un affievolimento, ma un vero fenomeno di
interferenza tra
m(t) e
^m(t). Per evitare che ciò accada, nella trasmissione blu è spesso presente una portante parzialmente soppressa, in modo da agevolare il funzionamento delle tecniche di recupero portante.
Anche nel caso
blr è possibile ricorrere ad un demodulatore di tipo omodina, evitando i problemi di sincronizzazione di fase illustrati, purché il filtro
H(f) usato in trasmissione per rimuovere parte di una banda laterale presenti alcune condizioni di simmetria attorno a
f0.
Le variazioni di ampiezza dei segnali
am-blu sono ben maggiori che nel caso
bld, a causa del brusco troncamento spettrale causato dal filtro di Hilbert, e dalla distorsione di fase non lineare associata, e di ciò va tenuto conto per evitare fenomeni di saturazione e distorsione non lineare (§
8.3), anche adottando adeguate contromisure.
12.2.7 Demodulatore eterodina
Individua la tecnica di utilizzare una frequenza di demodulazione
differente da quella della portante, e fu inventata per rendere udibili i segnali in
codice Morse trasmessi via radio in forma di una portante intermittente
f0: dato che
cosαcosβ = 1⁄2(cos(α + β) + cos(α − β)), scegliendo la frequenza di eterodina
fe di poco inferiore a quella della portante
f0 il termine a frequenza
f0 − fe cade infatti nella banda udibile. Da un punto di vista grafico il risultato equivale a
sommare e sottrarre la frequenza
eterodina alle frequenze dell’altro segnale, traslando così
f0 in
f0 ± fe: indichiamo di qui in poi la differenza
f0 − fe con il termine di
media frequenza fM, detta anche frequenza
intermedia o
if.
Piccola storia della radio
Con lo sviluppo della trasmissione radio di segnali modulati, le diverse emittenti eseguivano trasmissioni am-bld-pi ognuna su di una portante differente; sebbene fosse possibile sintonizzare ciascuna emittente con un demodulatore omodina centrato sulla relativa portante, i dispositivi del tempo soffrivano di fenomeni di deriva, e non essendo ancora stato inventato il pll, la portante di demodulazione slittava. Inoltre la tecnica omodina soffriva anche del problema del rientro della portante di demodulazione sull’altro ingresso del mixer, comportando l’insorgenza di una componente continua in uscita dal mixer stesso, in grado di mandare in saturazione il successivo stadio di amplificazione.
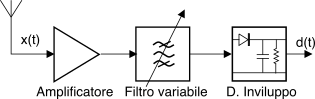
Si provò quindi ad adottare una modulazione a portante intera in modo da poter adottare un demodulatore ad inviluppo, ma in tal caso l’emittente desiderata doveva essere prima
selezionata anteponendo al demodulatore un filtro passa banda
variabile centrato sulla portante dell’emittente desiderata (vedi figura), filtro di difficile realizzazione all’aumentare della frequenza.
La serie di considerazioni sopra svolte portò alla scelta di adottare in modo sistematico la tecnica di demodulazione eterodina, detta
super- qualora si scelga una frequenza
intermedia
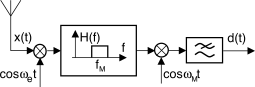
fM più elevata di quelle dello spettro udibile, dando luogo allo schema di ricevitore che potremmo definire
in due passi mostrato a lato: volendo sintonizzare l’emittente con portante
f0 il segnale ricevuto viene innanzitutto moltiplicato per una portante
eterodina fe = f0 − fM, in modo che lo spettro dell’emittente centrata su
f0 sia traslato alla
frequenza intermedia fM = f0 − fe. A quel punto un filtro passa banda
fisso centrato su
fM permette di isolare l’emittente desiderata, che viene successivamente portata in banda base ad opera dello stadio di demodulazione
omodina operante a frequenza
fM.
Da un punto di vista grafico accade quanto mostrato in figura, con la frequenza
fe
che viene
sommata e sottratta a tutte le frequenze in ingresso al primo mixer, portando in
fM l’emittente centrata su di una
f0 distante da
fe di una quantità pari alla loro differenza
f0 − fe.
La sintonia di una diversa emittente avviene variando esclusivamente
fe, e quindi
volendo ricevere ad esempio quella centrata in
f1, si imposta
fe = f1 − fM come mostrato in questa seconda figura, in modo che ora sia la seconda emittente
a cadere dentro il filtro centrato su
fM.
12.2.7.2 Frequenza immagine
In realtà un ricevitore eterodina prevede la presenza di un ulteriore filtro posto
prima del mixer con
fe, necessario ad evitare che in ingresso al filtro a media frequenza si presenti, oltre all’emittente centrata a
f0 = fe + fM, anche quella a portante
fi = fe − fM,
per la quale cioè
fe − fi = fM.
La frequenza fi prende il nome di frequenza immagine, in quanto è l’immagine speculare di f0 rispetto ad fe; in altre parole, l’utilizzo di una portante eterodina fe provoca la traslazione a media frequenza sia della emittente desiderata e centrata in f0 = fe + fM, sia della sua immagine a distanza 2fM, centrata in fi = fe − fM. Pertanto in ingresso al ricevitore va anteposto un filtro che elimini dal segnale di ingresso le frequenze immagine, ovvero, una volta nota la gamma di frequenze che si vuole sintonizzare, elimini tutte le trasmissioni centrate su portanti a frequenze minori di fe.
Scelta della frequenza di eterodina
Le trasmissioni
broadcast am adottano portanti nella regione di frequenze detta delle
onde medie (540-1600 KHz) con modulazione
am-bld-pi ed utilizzano un ricevitore per il quale si sceglie una
fe maggiore della frequenza
f0 da sintonizzare anziché
minore come prima illustrato, con il risultato che ora la frequenza immagine
fi è quella che si trova
al disopra della
f0, come mostrato
nello schema a lato. Per queste trasmissioni si è scelto di utilizzare una frequenza intermedia
fM pari a
455 KHz, quindi volendo ad esempio sintonizzare una emittente con
f0 = 600 KHz occorre una
fe = fM + f0 = 1055 KHz, ma allo stesso tempo anche l’emittente relativa alla portante
fi = fe + fM = 1510 KHz viene traslata nella banda del filtro a frequenza intermedia. Pertanto, prima del mixer operante ad
fe va posto un filtro che lasci passare solo le emittenti centrate a portanti inferiori ad
fe, reintroducendo l’esigenza di un filtro variabile, ma meno complesso di quello di pag.
1 dato che questo non ha lo scopo di filtrare una sola emittente, ma l’intera banda.
La scelta
fM = 455KHz, inferiore alla minima frequenza di
510 KHz, permette di utilizzare per la media frequenza una regione dello spettro libera da altre trasmissioni, che altrimenti potrebbero essere amplificate dagli stadi ad alto guadagno posti dopo il filtro
mf. La scelta di
fe > f0 permette poi di posizionare il filtro
passa banda che elimina le frequenze immagine
al disotto della
fe, rendendo più semplice la sua realizzazione. La figura
12.23 mostra lo schema generale (compresi gli stadi di amplificazione) per un ricevitore supereterodina con
fe > f0 .
Riassumiamo i vantaggi ottenuti:
- la sintonia avviene mediante la variazione di fe, ed il resto non cambia;
- la separazione tra f0 ed fM scongiura il rischio di instabilità che si potrebbe verificare se il segnale uscente dal filtro di media frequenza, amplificato, fosse ri-captato dallo stadio di ingresso, mentre ora invece l’amplificazione può aver luogo proprio nello stadio a media frequenza;
- il ridotto valore di fM rispetto alla banda di frequenze di cui si opera la sintonia permette la realizzazione di un filtro passa banda a media frequenza di ridotta complessità e migliore selettività;
- per un segnale a portante intera lo stadio omodina è sostituito da uno ad inviluppo, senza necessità di generare f0.
Conversione di frequenza multipla
Notiamo che lo stadio di eterodina può essere ulteriormente ripartito in due conversioni di frequenza successive (vedi ad es. la fig.
25.8 a pag.
1), di cui la seconda conversione opera la sintonia, mentre la prima ha il solo scopo di traslare la banda di interesse in una regione centrata su di una frequenza inferiore, in cui il mezzo trasmissivo (ad es. un cavo coassiale) presenta minore attenuazione. Inoltre, la tecnica di mixing eterodina viene utilizzata anche negli apparati ripetitori, in cui la frequenza di trasmissione deve differire da quella di ricezione per evitare fenomeni di auto-interferenza.
Dopo lo stadio di eterodina, il segnale centrato a media frequenza presenta un valore di frequenza massima
W assai ridotto rispetto alla sua versione modulata, permettendo di attuare su di esso le tecniche di (sotto)campionamento (§
4.8) ed operare le restati operazioni, come la demodulazione in fase e quadratura, in via completamente numerica. Dato che attualmente tutti i ricevitori operano in questo modo, la questione verrà approfondita in una futura edizione.