15.2 Scelta dell’impulso dati

15.2.1 Codici di linea a banda infinita

La figura a lato mostra lo spettro di densità di potenza P_x(f) calcolato per f che va da zero fino al doppio di f_b, per un segnale dati binario che ricade in una delle categorie illustrate di seguito, dette codici di linea. Il risultato è ottenuto generando i valori (0 o 1) per 400 simboli binari a_k in modo pseudo-casuale [729]   [729] La non perfetta indipendenza statistica dei simboli prodotti dal generatore di numeri casuali di un computer si può riflettere su di una ridotta generalità del risultato mostrato, che tuttavia rispecchia molto bene i casi reali., campionando il segnale dati (21.1) con 16 campioni per periodo di bit, e valutando con questi una stima spettrale [730]   [730] Ottenuta applicando ai dati una finestra triangolare (§ 3.8.4) e quindi valutando il periodogramma (§ 7.3.1). .

• NRZ o No Return to Zero: l’acronimo che lo descrive significa che il segnale “non torna a zero” per tutto il periodo di bit, essendo g(t) = rect_Tb(t); pertanto lo spettro G(f) è di tipo sinc(fT_b), con il primo zero a f = 1 ⁄ T_b, e presenta una componente continua. Rimane costante per dati costanti e ciò complica la sincronizzazione (§ 15.7) del clock del ricevitore stante l’assenza in questo caso di transizioni. La mancanza di energia per f = 1 ⁄ T_b aggrava inoltre la situazione anche per dati qualsiasi.
• RZ o Return to Zero: in questo caso l’impulso g(t) ha durata pari a T_b ⁄ 2, il segnale presenta (a parità di ampiezza) minore energia di NRZ, mentre lo spettro presenta una componente pronunciata esattamente a frequenza f_b, agevolando la sincronizzazione sul bit ma occupando una banda maggiore. Ma anche questo segnale si mantiene costante per lunghe sequenze di zeri.

Figure 15.12 Forme d’onda di esempio associate ai codici di linea descritti nel testo

• NRZ polare, RZ polare: realizzano l’impulso con polarità negativa quando associato ad un bit pari a zero, e presentano media nulla solo se i valori 0 ed 1 sono equiprobabili. RZ polare non è mai costante, facilitando il compito della sincronizzazione.
• Manchester [733]   [733] Vedi https://it.wikipedia.org/wiki/Codifica_Manchester: realizza una codifica di fase, in quanto usa un impulso RZ a piena dinamica, in salita od in discesa, in corrispondenza dei bit 1 e 0. Per questo motivo il segnale risulta sempre a media nulla. L’occupazione spettrale è intermedia tra il caso NRZ ed RZ, dato che la durata dell’impulso può essere T_b o ^T_b⁄₂. L’uso del codice Manchester è prescritto dallo standard ieee 802.3 per le LAN a bus con contesa di accesso cdma/cd (vedi § 23.1.4).
• AMI o Alternate Mark Inversion: codifica gli 1 con polarità alternate, mediante un impulso g(t) rettangolare di estensione T_b o T_b ⁄ 2, e gli zeri con assenza di segnale, garantendo assenza di valore medio. La caratteristica di alternare valori positivi e negativi gli fa meritare il nome di codice pseudo-ternario, e denota la presenza di memoria. Da un punto di vista spettrale, l’AMI esibisce una occupazione di banda [734]   [734] La densità spettrale mostrata in figura è relativa all’uso di una g(t) di tipo RZ. ridotta rispetto a RZ, per via dei periodi silenti corrispondenti agli zeri. Se il periodo silente è prolungato, l’assenza di transizioni può compromettere la sincronizzazione di bit, e per questo motivo sono stati definiti ulteriori codici derivati, come ad esempio l’HDB3 [735]   [735] La codifica hdb3 è utilizzata per trasmettere il segnale pcm a 2 Mbps (vedi § 24.3.1), e l’acronimo significa High-Density Bipolar-3-zeroes. Come per ami, rappresenta gli uni con polarità alternate, ma rimpiazza le sequenze di quattro zeri consecutivi forzando una violazione della regola dell’alternanza sull’ultimo bit dei quattro, in modo che il ricevitore, rilevando la violazione, è in grado di riportare il bit a zero. Dato però che la presenza della violazione creerebbe la comparsa di una componente continua nel segnale, sono inseriti anche dei bit di bilanciamento, per rimuovere quest’ultima. Questi si collocano al posto del primo dei quattro zeri, e la loro polarità è scelta in modo che la sequenza delle violazioni abbia un polarità alternata; in definitiva, dopo la prima violazione, si usa sempre anche il bit di bilanciamento..

• Manchester Differenziale: usa un impulso RZ a piena dinamica come per il Manchester, la cui polarità risulta però invertita rispetto all’impulso precedente se il nuovo bit è uno, mentre è mantenuta uguale nel caso arrivi uno zero (in corrispondenza delle frecce); pertanto, in presenza degli uni non si verifica transizione al confine tra i periodi di bit. Questa soluzione è utilizzata nel contesto dello standard ieee 802.5 per LAN Token Ring. L’occupazione spettrale è simile a quella osservabile per la codifica Manchester.
• NRZI: deriva dall’NRZ, e la I sta per Inverted. Ora il livello del segnale permane nello stesso stato per i bit pari ad uno, e cambia stato per i bit pari a zero. L’assenza di valor medio è legata alla statistica che descrive le sequenze di uni e dunque non può essere garantita, mentre permangono i problemi legati alla sincronizzazione. La ridotta occupazione spettrale lo rende però interessante.

15.2.2 Segnale dati limitato in banda

15.2.2.1 Requisiti per l’impulso di trasmissione

Ad esempio adottando g(t) =  rect_τ(t) con τ ≤ T_s il relativo spettro di ampiezza G(f) = τ sinc(fτ) presenta il primo passaggio per zero a frequenza 1τ ≥ 1T_s = f_s, e la densità di potenza P_x(f) può essere considerata nulla solo dopo diversi multipli di tale valore.

Il problema della limitazione di banda potrebbe essere risolto adottando un impulso elementare di tipo g(t) =  sinc(f_st) che, essendo f_s = ¹⁄_Ts, ha trasformata G(f) = T_s ⋅ rect_fs(f) strettamente limitata nella banda |f| < f_s2: in tal caso se il canale presenta un comportamento ideale in tale (limitato) intervallo di frequenze il segnale dati non subisce alterazioni. Ma lo svantaggio di adottare una forma d’onda g(t) limitata in frequenza è che la stessa è illimitata nel tempo, e dunque l’impulso può essere realizzato [738]   [738]  Il requisito di causalità h(t) = 0 per t < 0 (pag. 1) a cui deve sottostare qualsiasi sistema fisico impedisce infatti di realizzare un filtro la cui risposta impulsiva g(t) abbia una estensione temporale illimitata: per avvicinarsi al risultato desiderato occorre implementare il filtro adottando al posto di

g(t) una sua versione ritardata e limitata g’(t) = g(t − T_R) con t ≥ 0 e g’(t) = 0 altrimenti, come in figura.

Se T_R ≫ T_s, l’entità dell’approssimazione è accettabile, ed equivale ad un semplice ritardo pari a T_R; d’altro canto, quanto maggiore è la durata della risposta impulsiva, tanto più difficile (ossia costosa) risulta la realizzazione del filtro relativo.

solo in modo approssimato!

Contrariamente al caso del campionamento, ora non siamo interessati al valore del segnale negli istanti intermedi a quelli a cui sono centrati i simboli, e desideriamo unicamente recuperare i valori originali a_k. D’altra parte anche ammettendo di poter adottare una g(t) =  sinc(f_st) il recupero degli a_k può avvenire solamente campionando il segnale dati x(t) esattamente agli istanti t = nT_s,

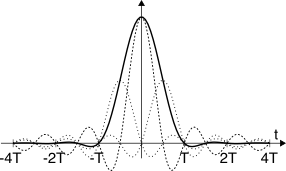
dato che al di fuori di tali istanti il valore del segnale dipende dal valore delle code degli impulsi g(t) centrati sugli altri simboli [739]   [739] Al contrario, se g(t) =  rect_Ts(t), il campionamento può avvenire ovunque nell’ambito del periodo di simbolo, ma si torna al caso di elevata occupazione di banda. come mostrato in figura, in cui la linea spessa rossa rappresenta il segnale dati x(t) risultato della somma dei contributi di termini a_k sinc(f_s(t − kT_s)) con a_k = ±1. L’orologio (clock) del ricevitore deve quindi comandare il campionatore esattamente agli istanti kT_s, e non in anticipo o in ritardo, perché altrimenti si verifica isi, tanto maggiore e da parte di tanti più simboli anche lontani, quanto più lentamente si attenuano le code della g(t). Dato però che nessun oscillatore ha una precisione infinta e che anzi i metodi di sincronizzazione (§ 15.7) presentano piccole variazioni (jitter) della loro frequenza, occorre ricercare una soluzione per g(t) che pur rimanendo limitata in banda presenti oscillazioni di ampiezza ridotta, in modo da tollerare meglio modesti errori di precisione nella determinazione degli istanti di campionamento.

1. occupare una banda contenuta;
2. ricorrere ad un filtro con g(t) di durata ridotta e quindi poco complesso;
3. ridurre la sensibilità agli errori di campionamento.

15.2.2.2 Criterio di Nyquist per l’assenza di ISI

Torniamo a riferirci alla (21.1) per osservare che, affinché x(t = nT_s) dipenda dal solo valore a_n e non dagli altri a_k con k ≠ n, deve risultare

(21.3) g(t) = ⎧⎪⎨⎪⎩ 1   se t = 0     0    se t = mT_s  con m ≠ 0     ∀     altrove

cond. di Nyquist nel tempo

e cioè g(t) deve passare da zero in tutti gli istanti multipli di T_s, tranne che per t = 0 dove deve valere 1, mentre per valori di t intermedi può assumere qualunque valore. In tal caso infatti dalla (21.1) si ottiene:

x(nT_s) = ⎲⎳_k a_k ⋅ g(nT_s − kT_s) = ⎲⎳_k a_k ⋅ g((n − k)T_s) = a_n

dato che m = n − k è un intero che vale zero solo quando k = n. Le condizioni (21.3) prendono il nome di condizioni di Nyquist per l’assenza di interferenza intersimbolo (isi) nel dominio del tempo. Se una forma d’onda g(t) soddisfa tali condizioni, allora viene detta impulso di Nyquist( [741]   [741] Ad esempio, l’impulso rettangolare è di Nyquist, in quanto rect_Ts(t) = ⎧⎨⎩ 1 se |t| < T_s2     0 se t = kT_s .).

Dalle condizioni di Nyquist nel tempo (21.3) se ne derivano altre in frequenza, mediante i seguenti passaggi. Moltiplicando g(t) per un treno di impulsi π_Ts(t) = ∑_k δ(t − kT_s) si ottiene

g(t) ⋅ π_Ts(t) = δ(t)

dato che g(nT_s) = 0 e g(0) = 1. Trasformando (vedi eq. (10.61)) si ottiene:

1 = G(f) * 1T_s ⋅ Π_1Ts(f) = G(f) * 1T_s ⋅ ⎲⎳_k δ(f − k1T_s)

Indicando con f_s = 1T_s la frequenza di simbolo, ed eseguendo la convoluzione tra G(f) e gli impulsi centrati in f = kf_s, risulta infine

(21.4) ⎲⎳_k G(f − kf_s) = T_s

che rappresenta la condizione in frequenza per l’assenza di interferenza intersimbolo.

condizioni di Nyquist in frequenza

Il risultato ottenuto si interpreta considerando che una qualunque G(f) va bene purché, se sommata con le sue repliche traslate di multipli di f_s, dia luogo ad una costante, ovvero se G(f) manifesta simmetria dispari rispetto ad ^f_s⁄₂. In tal caso G(f) può essere descritta come la risposta in frequenza di un filtro di Nyquist. Notiamo che seppure G(f) possa essere qualsiasi, anche non limitata in banda, il nostro interesse è appunto per le G(f) limitate in banda, come quella triangolare dell’esempio a fianco.

15.2.2.3 Filtro a coseno rialzato

Descrive una famiglia parametrica di filtri di Nyquist limitati in banda, detti a coseno

rialzato in quanto la G(f) è realizzata mediante 2 semiperiodi di coseno raccordati da una retta, come mostrato a lato. La fig. 15.19-a)( [742]   [742] La fig. 16.4 a pag. 1 mostra la stessa funzione su di una scala quadratica e in decibel.) illustra l’andamento di G(f) per diverse scelte del parametro 0 < γ < 1 chiamato coefficiente di roll-off [743]   [743] Il termine roll-off può essere tradotto come “rotola fuori “., che rappresenta l’indice di dispersione del ramo di coseno attorno alla frequenza ^f_s⁄₂, detta frequenza di Nyquist [744]   [744] Molto intimamente legata alla velocità di Nyquist definita al § 4.1 come la minima frequenza di campionamento f_c = 2W per un segnale analogico di banda W, mentre la frequenza di Nyquist si riferisce invece a metà della massima frequenza di segnalazione ^f_s⁄₂ = B per un segnale dati che transita su di un canale limitato in banda B, per motivi presto chiari. Come evidente due aspetti dello stesso fenomeno, ma in contesti differenti, vedi https://en.wikipedia.org/wiki/Nyquist_rate..

a)

b)

Figure 15.19 a) - filtro a coseno rialzato e b) - impulso di Nyquist per f_s = 0.5, variando γ

La banda occupata a frequenze positive da G(f) può quindi essere espressa in funzione di γ come

(21.5) B = f_s2(1 + γ) = f_b2log₂L(1 + γ)

e varia da un minimo B|_γ = 0 = f_s ⁄ 2 in corrispondenza di un G(f)|_γ = 0 = T_s rect_fs(f) rettangolare, ad un massimo pari a B|_γ = 1 = f_s a cui corrisponde una

Il caso di γ = 0 individua una G(f) = T_s rect_fs(f) e come già discusso a pag. 1 corrisponde ad un impulso g(t) = sinc(f_st).

Tale scelta viene detta a banda minima poiché non è possibile occupare una banda inferiore, dato che in tal caso non sarebbero verificate le condizioni di Nyquist in frequenza, in quanto nella (21.4) resterebbero dei “buchi”.

In questo caso per g(t) si può ottenere l’espressione generale [745]   [745] Non ho trovato questi passaggi già svolti in nessun posto, qualche lettore può aiutare? Tutto quel che sono riuscito a calcolare è relativo al caso γ = 1, per cui g(t) = F^− 1⎧⎩T2[1 + cos(πTf)]⎫⎭ ⋅ rect_²⁄T(f) che fornisce

g(t)  = T2⎡⎣δ(t) + 12δ⎛⎝t − T2⎞⎠ + 12δ⎛⎝t + T2⎞⎠⎤⎦ * 2T sinc⎛⎝2Tt⎞⎠ =       =  sinc⎛⎝2Tt⎞⎠ + 12 sinc⎛⎝2T ⎛⎝t − T2⎞⎠⎞⎠ + 12 sinc⎛⎝2T ⎛⎝t + T2⎞⎠⎞⎠

che una volta graficato, conferma l’andamento di fig. 15.19. Osserviamo che per t → ¹⁄_2γfs il denominatore di (21.6) si annulla, ma lo stesso avviene anche per il numeratore, che in tal caso tende a cosπ2, dando luogo alla forma 00, ed il cui limite sembra tendere a poco meno di uno.

(21.6) g(t) =  sinc(f_st) ⋅ cos γπtf_s1 − (2γtf_s)²

a cui corrisponde una forma d’onda simile a sinc(f_st), ma che va a zero molto più rapidamente, come verificabile osservando la parte destra di Fig. 15.19. Pertanto se γ → 1 le oscillazioni di g(t) sono molto più smorzate, ed anche in presenza di errori negli istanti di campionamento t = kT_s ogni impulso estende la sua influenza ad un numero di simboli limitrofi molto ridotto rispetto al caso γ = 0.

Figure 15.23 Segnale dati e diagramma ad occhio per diversi valori di roll-off

Per verificare visivamente quanto affermato, aiutiamoci con la fig. 15.23 che in alto a sinistra mostra l’andamento di un segnale dati realizzato adottando la g(t) fornita dalla (21.6), calcolata per γ = 0.5, e per simboli a_k a due valori, pari a 0 e 1. Notiamo che al di fuori degli istanti di simbolo t = kT_s il segnale può assumere valori arbitrari, anche oltre la dinamica degli a_k. La rappresentazione fornita dal diagramma ad occhio per questo segnale dati, mostrato in alto a destra in fig 15.23, permette di valutare meglio la precisione di temporizzazione che è necessaria per evitare isi, e che è pari a metà della apertura orizzontale dell’occhio.

Licenza Creative Commons BY-NC-SA	Ottieni il PDF o la Stampa Storia Blog
	Trasmissione dei Segnali e Sistemi di Telecomunicazione è un progetto ventennale di cultura libera evoluto fino alla forma attuale
Come vedi non c'è traccia di pubblicità, ma in compenso adoriamo le Donazioni