Sezione 17.3: Capacità di canale continuo Su Capitolo 17: Capacità e codifica di canale Sezione 17.5: Verso il limite di Shannon 

17.4 Codifica di canale

Dopo aver analizzato i risultati che la teoria dell’informazione fornisce a riguardo delle migliori prestazioni ottenibili, proseguiamo il discorso iniziato al § 15.6.2.1 su come aggiungere ridondanza ad un flusso binario a velocità fb da trasmettere su di un canale numerico, in modo da realizzare una protezione fec capace di ridurre la probabilità di errore per bit Pe in ricezione. Ricordiamo che al § 17.2 abbiamo mostrato come, aumentando il ritardo di codifica, la probabilità di errore può essere resa piccola a piacere, purché fb = R < C, essendo C la capacità di canale. Mentre una soluzione basata su segnalazione ortogonale (ad esempio, l’fsk del § 16.5.1) determina un aumento asintoticamente esponenziale della banda occupata [938]   [938] Infatti partendo dall’espressione della banda occupata dall’fsk B → fb2 ⋅ Llog2L (eq. (21.54)) e considerando che L = 2M = 2fbT si ottiene B = 12T ⋅ 2fbT ovvero un aumento esponenziale di B al crescere di T. Un diverso esempio può essere l’uso di forme d’onda ortogonali realizzate come rectT⁄L posti all’interno del periodo di simbolo T in modo che non si sovrappongano se associati a simboli diversi (vedi fig. 7.20 a pag. 1). Anche qui, aumentando T il numero di simboli L = 2M = 2fbT aumenta esponenzialmente, e la durata T⁄L = T⁄2fbT di ogni rect tende esponenzialmente a zero se T → ∞, mentre la banda occupata tende ad infinito, sempre con legge esponenziale rispetto a T., le tecniche illustrate nel seguito consentono di mantenere la relazione tra grado di protezione e banda occupata di tipo proporzionale.
Classificazione delle tecniche di codifica di canale
Una categoria molto vasta è quella dei codici a blocco, che operano suddividendo il messaggio da proteggere in blocchi disgiunti, codificati in modo indipendente; una diversa classe è quella dei codici convoluzionali, che invece trattano il messaggio come una sequenza priva di suddivisioni, da cui calcolare una nuova sequenza (a velocità maggiore) che ne rappresenta la codifica. Mentre i codici convoluzionali sono descritti al § 17.4.2, la trattazione dei codici a blocco è iniziata al § 15.6.2.1, che si suggerisce di consultare prima di proseguire, riassumendone qui solo alcuni concetti.
Tasso di codifica, velocità binaria ed Eb⁄N0
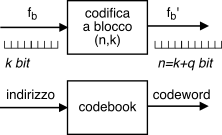
Riprendiamo la notazione introdotta al § 15.6.2.1 per i codici a blocco, in cui ad ogni k bit della sequenza di ingresso (da proteggere)
figure f4.19b.png
si genera una codeword [939]   [939] Si ricorda che l’insieme delle 2k codeword costituisce un codebook. con lunghezza n = k + q > k bit, in cui sono stati aggiunti q bit di protezione in funzione dei k del blocco: tale procedura viene indicata come codice (n, k), la cui efficienza è misurata dal tasso di codifica (o code rate)
Rc = kn < 1
che rappresenta la frazione di bit informativi sul totale di quelli trasmessi, nonché l’inverso del fattore di espansione di banda [940]   [940] Notiamo la differenza tra queste tre grandezze dall’aspetto simile: l’efficienza spettrale ρ = fb⁄B indica quanto una tecnica di modulazione numerica faccia buon uso dello spettro, il rapporto BR esprime l’inverso del grado di utilizzo della banda B di un canale numerico, mentre Rc = k⁄n misura l’efficienza del codice adottato.: la nuova velocità di trasmissione in presenza di codifica vale infatti
f’b = fbRc
Osserviamo che all’aumento della velocità di segnalazione (essendo f’b > fb) corrisponde una eguale diminuzione del rapporto Eb⁄N0 =  PxN0f’b = RcPxN0fb, e conseguentemente si assiste ad un peggioramento della probabilità di errore grezza del decisore: pertanto, la capacità correttiva del codice deve essere tale da compensare anche questo aspetto. Per mantenere limitato l’effetto descritto, così come l’espansione di banda, vorremmo trovare codificatori per cui Rc sia il più possibile vicino ad uno.
Distanza di Hamming, distanza minima e capacità correttiva
Al § 391 è stata definita dH(xi, xj) come il numero di bit in cui le codeword xi e xj differiscono, pari al numero di errori sul bit necessario affinché una si trasformi nell’altra. Valutando la distanza di Hamming dH tra tutte le possibili coppie di codeword, si definisce la distanza minima del codice dm = mini ≠ j dH(xi, xj), che descrive quanto le codeword siano vicine nel caso peggiore.
Esempio Con k = 4 e q = 3 esistono 24 = 16 codeword su 27 = 128 possibili configurazioni degli n = k + q bit della codeword. Ciò significa che ci sono 23 = 8 non-codeword per ogni codeword. Sarebbe bene scegliere queste ultime in modo che risultino distanti (nel senso di Hamming) l’una dall’altra!
Come discusso al § 393, la capacità di correzione del codice è direttamente legata alla minima distanza dm, sussistendo le relazioni
Un codice è tanto più potente quanti più errori è in grado di correggere, e dunque deve possedere dm elevato. In un codice a blocchi (n, k) i k bit del messaggio originale assumono tutte le configurazioni possibili, e quindi contribuiscono alla distanza tra codeword per un solo bit; per ottenere dm > 1 occorre pertanto sfruttare gli n − k = q bit di protezione, portando a scrivere
dm ≤ q + 1 = n − k + 1
che evidenzia la relazione tra dm e la quantità di bit aggiunti q. L’uguaglianza sussiste solo per una particolare classe di codici [941]   [941] Indicati come codici mds, vedi http://en.wikipedia.org/wiki/Singleton_bound#MDS_codes. tra cui il codice a ripetizione, discusso al § 15.6.2.2, che adottando una dimensione di blocco in ingresso k = 1 ha però un tasso di codifica Rc = k⁄n = 1⁄n molto inefficiente.
Guadagno di codifica Gc
La distanza dm ed il tasso Rc non possono essere scelti
figure f17.19.cg.png
indipendentemente, dato che per aumentare dm occorre aumentare i bit di protezione q, a cui corrisponde una diminuzione del valore di Rc. Una quantità che tiene conto di entrambi i termini è il guadagno di codifica asintotico
(21.105) Gac = dmRc
che esprime il fattore di aumento della potenza di segnale che avrebbe prodotto lo stesso miglioramento in termini di Pe dovuto all’adozione del codice.
Esempio Se Gc = 2 significa che l’uso del codice porta ad un valore di Pe pari a quello ottenibile con una trasmissione a potenza doppia, ma non codificata.
Tale risultato è valido nel caso di soft-decoding [942]   [942] Nel caso di decisioni hard o bit a bit, si ottiene una espressione del tipo Gac, hard = Rc(t + 1), in cui t è il numero di bit per parola che il codice è in grado di correggere. (pag. 1), ed è aggettivato come asintotico in quanto è valido solo per valori di Eb⁄N0 elevati: infatti all’aumentare della potenza di rumore, per qualunque codice e metodo di decisione il valore di Gc si riduce, fino a divenire inferiore ad uno, quando gli errori sono così numerosi da non poter più essere corretti.
Mostriamo ora soluzioni che consentono di ottenere un adeguato potere di correzione, senza per questo aumentare di molto la velocità di trasmissione del flusso codificato.

17.4.1 Codifica a blocco

Le proprietà di questa classe di codici possono essere meglio analizzate interpretando l’insieme delle possibili codeword da un punto di vista algebrico, ed adottando una notazione matriciale idonea a descrivere la classe di codici a blocco, mentre per la sottoclasse dei codici ciclici (§ 17.4.1.2) interviene una notazione polinomiale.
Iniziamo ricordando che il codebook (§ 15.6.2.1) di un codice a blocco (n, k) è composto da sequenze di n bit indicate come codeword x espresse mediante un vettore ad elementi binari
x = (x1 x2 ⋯ xn)
che può assumere solo 2k diversi valori tra i 2n possibili, mentre le ricezione di una delle rimanenti 2n − 2k combinazioni di bit segnala la presenza di almeno un errore. Ad esempio per un codice a ripetizione 3:1 (§ 15.6.2.2, in cui k = 1 ed n = 3) vi sono solo due codeword con vettori x1x2x3 pari a 000 ed 111, mentre le restanti 8-2=6 configurazioni non sono codeword.
Codice lineare
Un codebook (che implementa un codice) è detto lineare se le sue 2k codeword costituiscono uno spazio lineare (§ 2.4.2), ovvero se comprendono la codeword nulla, e la somma di due codeword è anch’essa una parola di codice. La somma tra due codeword è definita in base alla matematica binaria modulo due, ovvero espressa mediante l’operatore di or esclusivo bit a bit ⊕ come
(21.106)
x + y = (x1 ⊕ y1   x2 ⊕ y2   ⋯   xn ⊕ yn)
Notiamo incidentalmente che, in virtù dell’algebra modulo 2 indotta dall’operatore ⊕, la somma tra vettori binari produce un nuovo vettore con elementi pari ad uno nelle posizioni in cui essi differiscono, dunque in numero pari alla dH tra i vettori.
Distanza dm per codici lineari
Definiamo ora peso w(z) di una codeword z il numero di uni in essa contenuti, ovvero la sua distanza di Hamming rispetto alla cw nulla, cioè w(z) = dH(z, 0). Per un codice lineare la minima distanza del codice dm può essere valutata come il minimo peso tra tutte le codeword non zero [943]   [943] Infatti dalla definizione di somma tra cw otteniamo che dH(x, y) è pari al peso w(z) della codeword z = x + y, ossia z presenta componenti zj = 1 solo in corrispondenza di elementi xj ≠ yj. Ma per la linearità anche z appartiene al codebook, ovvero sommando tra loro tutte le possibili coppie ottengo l’intero codebook, e dunque la ricerca su tutte le coppie si trasforma in una ricerca su tutte le codeword., ossia
dm =  minz ≠ 0  [w(z)]
Codice sistematico e rappresentazione matriciale
Con il termine sistematico si intende un codice che ottiene gli n bit delle codeword x concatenando per primi i k bit da proteggere, indicati con m, a cui seguono i q = n − k bit di protezione, indicati con c. Ovvero come abbiamo implicitamente assunto fino ad ora, anche se si tratta
figure f4.19e.png
di una scelta per nulla scontata. Mostreremo più sotto che un codice sistematico è anche lineare; le sue codeword vengono quindi scritte nella forma
x = (m1 m2 ⋯ mk c1 c2 ⋯ cq)
ovvero come un vettore riga partizionato x = (m| c), in modo da poterlo calcolare a partire dal vettore m dei bit da proteggere moltiplicando lo stesso per una matrice generatrice [944]   [944] Questa fantomatica matrice generatrice che cala dall’alto in realtà ha una genesi ben razionale.
Se infatti definiamo una base ortogonale {ui} per lo spazio k − dimensionale descritto da tutti i possibili vettori m come i k vettori con componenti tutte nulle tranne quella in posizione i − esima e pari ad 1, possiamo allora scrivere un generico vettore m con componenti binarie mi come una combinazione lineare di vettori della base, ovvero m = ∑ki = 1 miui.
Indicando ora con gi la codeword (di n elementi) associata a ciascun vettore ui, otteniamo che ad un generico vettore m è associata la codeword x = ∑ki = 1 migi = m ⋅ G, in cui G è la nostra matrice generatrice di dimensione k × n le cui righe sono pari alle codeword gi con i = 1, 2, ⋯, k associate ai vettori della base ui.
k × n con struttura generale G = [Ik| P], in cui Ik è una matrice identità k × k e P è una sotto-matrice di elementi binari k × q. Le codeword si ottengono quindi come x = m ⋅ G, ovvero
(21.107)
[ m1  ⋯  mk  c1  ⋯  cq ] = [ m1  ⋯  mk ] ⋅ ⎡⎢⎢⎢⎣ 1  ⋯   0 p11   ⋯    p1q             ⋮  1⋮ ⋮ ⋱ ⋮             0  ⋯ 1 pk1 ⋯ pkq ⎤⎥⎥⎥⎦
in modo che P produca i q bit di protezione come c = m ⋅ P, in cui sono valide le normali regole di moltiplicazione tra matrici, tranne per l’accortezza di usare la somma modulo due anziché quella convenzionale. Il valore della (generica) j-esima (j = 1, 2, ⋯, q) componente di c si calcola pertanto come
cj =  m1 ⋅ p1j ⊕ m2 ⋅ p2j ⊕ ⋯ ⊕ mk ⋅ pkj
in cui il prodotto tra cifre binarie equivale all’operatore logico di and.
Esempio Se poniamo m = (1 0 1) e p = (0 1 1) il relativo prodotto interno vale
m ⋅ p  =  0 ⋅ 1 ⊕ 1 ⋅ 1 ⊕ 1 ⋅ 0 ⊕ 0 ⋅ 1 ⊕ 1 ⋅ 1  =  0 ⊕ 1 ⊕ 0 ⊕ 0 ⊕ 1  =  0
In definitiva ciascuna colonna di P individua un sotto-insieme di elementi di m su cui calcolare una somma di parità, fornendo il motivo per cui questo sotto-blocco di matrice G è rappresentato dalla lettera P. Ma non è ancora stato detto nulla che ci possa aiutare a scegliere i coefficienti pij allo scopo di ottenere i valori dm e Rc desiderati: il codice di Hamming (§ 17.4.1.1) ci fornisce una possibile soluzione.
Linearità di un codice sistematico
La linearità di un codebook sistematico può essere verificata se riusciamo a mostrare che la somma di due qualunque codeword è ancora una parola del codebook. A tale scopo, dato che la somma modulo due tra vettori binari x1 ⊕ x2 avviene bit per bit (eq. (21.106)), consideriamo le due parti m e c di una codeword x in modo indipendente. Dato che m può assumere una qualunque delle 2k configurazioni possibili, è sempre vero che m3 =  m1 ⊕ m2 appartiene allo stesso insieme. Per quanto riguarda i q bit di protezione c, osserviamo che
c3 =  c1 ⊕ c2 =  m1 P ⊕ m2 P = (m1 ⊕ m2) P
e dunque c3 corrisponde alla protezione di m3, ovvero x3 = ( m3|  c3) è una codeword esistente.

17.4.1.1 Codice di Hamming

E’ un codice a blocco (n, k) sistematico e lineare che permette di conseguire un tasso di codifica elevato pur mantenendo un buon potere correttivo. Aggiunge q ≥ 3 bit di controllo ai k bit informativi per formare codeword di lunghezza complessiva
n = 2q − 1
ottenendo un tasso di codifica pari a
Rc = kn = n − qn = 1 − q2q − 1
q n k Rc
3 7 4 0.57
4 15 11 0.73
5 31 26 0.84
6 63 57 0.9
7 127 120 0.94
che aumenta con il crescere di q, come mostrato in tabella. Le sue codeword si individuano ponendo le k righe della sottomatrice P pari a tutte le parole di q bit con due o più uni, in qualsiasi ordine. Ma la cosa ancora più simpatica è che per un codebook siffatto si ottiene una distanza di Hamming minima dm = 3, indipendentemente dalla scelta di q.
Esempio:  codice di Hamming (7, 4). Corrisponde al caso più semplice di scegliere q = 3, e dunque n = 23 − 1 = 7 e k = 7 − 3 = 4. Una possibile matrice generatrice è pari a
G = ⎡⎢⎢⎢⎢⎢⎣ 1 0 0 0         0 1 0 0         0 0 1 0         0 0 0 1 ||||||| 1 0 1       1 1 1       1 1 0       0 1 1 ⎤⎥⎥⎥⎥⎥⎦
a cui corrispondono le seguenti 24 = 16 codeword, per ognuna delle quali si è evidenziato il peso w(x), confermando che dm = 3.
Correzione basata sulla distanza
figure f4.19d.png
Indichiamo ora con y la parola di codice ricevuta; in presenza di errori, risulta y ≠ x. Il metodo diretto per rivelare ed eventualmente correggere gli errori presenti è quello di confrontare gli n bit ricevuti con tutte le possibili 2k codeword, e se nessuna di queste risulta uguale ad y, scegliere la x̂ con la minima distanza di Hamming, ossia quella per la quale il peso w(y ⊕ x̂) è minimo, ovvero
x̂ =  argminx{w(y ⊕ x)}
Correzione basata sulla sindrome
Un metodo che non richiede una ricerca esaustiva si basa invece sul calcolo della cosiddetta sindrome, ottenuta mediante moltiplicazione del vettore y ricevuto per una matrice n × q di controllo parità H, definita come H = ⎡⎣PIq⎤⎦ in cui P è la stessa matrice di parità utilizzata nella matrice generatrice G, e Iq è una matrice identità di dimensioni q × q. La matrice H esibisce la simpatica proprietà [945]   [945] In effetti la simpatia c’entra ben poco, ed H è costruita in modo che le sue q colonne siano ortogonali a tutte le k righe di G (oltre che tra loro), individuando così una base di rappresentazione per il sottospazio di dimensione 2q complemento ortogonale di quello di dimensione 2k descritto dalle codeword di lunghezza n = k + q. La dimostrazione che ho trovato (per provare che per codici sistematici il risultato è quello mostrato nel testo) contiene un errore, e non la cito. che, se moltiplicata per una qualunque codeword valida, fornisce un vettore nullo di dimensione q, ossia
(21.108) x ⋅ H = (0 0 ⋯ 0)
Al contrario, se moltiplicata per un vettore y non appartenente al codebook, fornisce un vettore detto sindrome s = y ⋅ H non nullo, e quindi il suo calcolo permette la rivelazione (nei limiti consentiti da dm) dell’occorrenza di errori.
H =  ⎡⎢⎢⎢⎢⎢⎣ 1 0 1 1 1 1 1 1 0 0 1 1 1 0 0 0 1 0 0 0 1 ⎤⎥⎥⎥⎥⎥⎦
Esempio considerando di nuovo il caso di q = 3, la corrispondente matrice di controllo parità H = ⎡⎣PIq⎤⎦ è mostrata a lato. E’ facile verificare che per tutte le possibili codeword x (ad es. x = [0100111]) si ottiene x ⋅ H = [000]. Poniamo ora che si verifichi una sequenza di errore e = [0010010], dando luogo alla ricezione della parola y = x ⊕ e = [0110101]: per essa si ottiene una sindrome s = y ⋅ H = [100].
Per quanto riguarda la correzione, iniziamo scrivendo il vettore ricevuto come y = x ⊕ e, dove e è un vettore di n bit le cui componenti sono diverse da zero in corrispondenza dei bit errati di y. Il calcolo della sindrome fornisce allora
s = y ⋅ H = (x ⊕ e) ⋅ H = x ⋅ H ⊕ e ⋅ H = e ⋅ H
visto che come espresso dalla (21.108), la sindrome delle codeword è nulla. Ma dato che la sindrome ha dimensione di q elementi, tutte le 2n possibili sequenze di errore e danno luogo a sole 2q diverse sindromi, e quindi la conoscenza della sindrome non consente di risalire direttamente ad e. Osserviamo però che, riprendendo i risultati esposti al § 15.6.1.1, la probabilità P(m, n) che si siano verificati m errori su n bit decresce al crescere di m,  e pertanto il vettore ê che con maggior probabilità ha prodotto ognuna delle 2q sindromi s ≠ 0, è quello (tra tutti quelli che producono la stessa s) con il minor peso:
ê =  argmine : e ⋅ H = s {w(e)}
Osserviamo inoltre che il vettore di errore più probabile e con peso minimo è quello con un solo bit diverso da zero; indichiamo tali n possibili vettori di errore come ei (i = 1, 2, ⋯, n), qualora solo l’i − esimo bit (di n) sia pari ad uno. Accade poi che (per costruzione) la sindrome si associata ad ei, calcolata come si = ei ⋅ H, corrisponda esattamente all’i − esima riga tra le n righe di H. Pertanto l’indice i della riga che corrisponde alla sindrome calcolata, identifica l’indice del bit che ha subito errore.
Notiamo infine che se si verificano più errori di quanti dm permetta di correggere, è inutile (anzi dannoso) cercare di eseguire la correzione, perché il numero di errori complessivo può risultare ancora più elevato. Nel caso del codice di Hamming in cui dm = 3 si può correggere un solo errore per codeword, in accordo alla procedura discussa. Se invece e contiene due errori, la sua moltiplicazione per H produce comunque una delle 2q possibili sindromi, ed il tentativo di correzione produce un vettore x̂ contenente tre errori.
Esempio Un gruppo di bit 1001 è protetto dal codice di Hamming di pag. 1 producendo x = 1001110, mentre in ricezione si osserva y = 1101110. Il calcolo della sindrome s = y ⋅ H fornisce il risultato s = 111, che corrisponde alla seconda riga di H, ovvero al vettore di errore ê = 0100000, cioè proprio quello che si è verificato. Se invece avvengono due errori, e si riceve ad es. y = 1111110, si ottiene s = 101, a cui corrisponde ê = 1000000, e quindi il calcolo x̂ = y ⊕ ê produce ora x̂ = 0111110, che appunto contiene tre errori.
Esercizio Un flusso binario con codifica di Hamming (31, 26) è affetto da Pe = 10 − 4. Determinare la probabilità residua di errore sul bit (pag. 1) dopo decodifica. Risposta La presenza di un solo errore nella codeword viene corretta, mentre con due errori la correzione basata sulla sindrome ne sbaglia tre; il caso con più di due errori si considera improbabile, vedi § 15.6.1.1. La prob. di 2 errori su 31 è (eq. (21.27)) pari a P(2, 31) ≃ 31 ⋅ 302 (Pe)2 = 4.65 ⋅ 10 − 6, e l’evento di errore comporta 3 bit errati su 26 decodificati, dunque per la Pbite residua si ottiene come 326 ⋅ 4.65 ⋅10 − 6 = 5.36 ⋅ 10 − 7.

17.4.1.2 Codice ciclico

Anche questo appartiene alla famiglia dei codici lineari a blocco, con la condizione aggiuntiva che se x = (x1, x2, ⋯, xn) è una codeword lo sono anche tutti i suoi scorrimenti ciclici [946]   [946] Ad esempio, il codice [000, 110, 101, 011] è un codice ciclico, mentre [000, 010, 101, 111] no. Notiamo che gli scorrimenti della codeword 000, sono la codeword stessa., ovvero le codeword
x(1) = (x2, x3, ⋯, x1),     x(2) = (x3, x4, ⋯, x2),     ⋯,     x(n) = (xn, x1, ⋯, xn − 1)
In tal caso sussistono delle proprietà algebriche aggiuntive che si basano sulla teoria dei campi di Galois [947]   [947] http://it.wikipedia.org/wiki/Campo_finito, i cui elementi sono polinomi
x(p) = x1pn − 1 + x2pn − 2 + ⋯ + xn − 1p + xn
nella variabile p, con coefficienti binari definiti a partire dagli elementi delle codeword x; per tale motivo, i codici ciclici sono detti anche codici polinomiali [948]   [948] Si veda http://en.wikipedia.org/wiki/Polynomial_code: senza volerci addentrare nei particolari della teoria [949]   [949] http://en.wikipedia.org/wiki/Cyclic_code, citiamo direttamente i principali risultati.
Un codice ciclico (n, k) è completamente definito a partire da un polinomio generatore
g(p) = pn − k + g2pn − k − 1 + ⋯ + gn − kp + 1
di grado n − k che deve essere un divisore di pn + 1, ovvero tale che pn + 1⁄g(p) = q(p) con resto nullo [950]   [950] Si applicano le regole di divisione tra polinomi http://it.wikipedia.org/wiki/Divisione_dei_polinomi. Una volta definito g(p) è possibile ottenere la matrice generatrice G del codice in forma sistematica G = [Ik| P], calcolando le k righe di P come i coefficienti del polinomio resto della divisione tra pi e g(p), con i = n − 1, n − 2, ⋯, n − k.
Esempio Troviamo la matrice generatrice in forma sistematica per un codice ciclico (7, 4). Osserviamo innanzitutto che pn + 1 si fattorizza come p7 + 1 = (p + 1)(p3 + p2 + 1)(p3 + p + 1), e scegliamo g(p) = p3 + p2 + 1 come polinomio generatore. Il calcolo di pi⁄p3 + p2 + 1 per i = 6, 5, 4, 3 fornisce come resti i polinomi p2 + p, p + 1, p2 + p + 1, p2 + 1, pertanto la matrice generatrice risulta G = ⎡⎢⎢⎢⎢⎢⎣ 1 0 0 0         0 1 0 0         0 0 1 0         0 0 0 1 ||||||| 1 1 0       0 1 1       1 1 1       1 0 1 ⎤⎥⎥⎥⎥⎥⎦. Osserviamo che, a parte una permutazione, le righe di P sono le stesse di quelle che definiscono il codice di Hamming di pag. 1: infatti, Hamming rientra anche nella classe dei codici ciclici.
D’altra parte nel caso di un codice ciclico le codeword x associate ai bit m da proteggere si possono ottenere non solo utilizzando G come descritto dalla (21.107), ma anche in base alla seguente proprietà: indicando con
m(p) = m1pk − 1 + m2pk − 2 + ⋯ + mk − 1p + mk
il polinomio associato ai k bit da codificare, il polinomio associato alla corrispondente codeword x si ottiene come il prodotto x(p) = m(p) ⋅ g(p), e quindi gli elementi xi della codeword sono individuati calcolando la convoluzione discreta [951]   [951] Il valore dei coefficienti del polinomio prodotto è indicato anche come prodotto di Cauchy (vedi http://it.wikipedia.org/wiki/Prodotto_di_Cauchy), e che si ottenga come una convoluzione è facilmente verificabile: dati ad es. a(p) = a0 + a1p + a2p2 e b(p) = b0 + b1p, si ottiene c(p) = a0b0 + (a0b1 + a1b0)p + a2p2 = ∑2i = 0pi∑2j = 0ajbi − j. La notazione lievemente diversa del testo, è dovuta al diverso modo di indicizzare i coefficienti. tra i coefficienti di m(p) e g(p): xi = ∑kj = 1mjgi − j + 1 per i = 1, 2, ⋯, n, operazione che può essere realizzata mediante un filtro fir con coefficienti dati dai valori gi.
Notiamo infine che nel testo si è già incontrato un codice polinomiale (e quindi ciclico) al § 15.6.3.3 a proposito del crc: i q bit di protezione possono quindi essere anche ottenuti mediante l’utilizzo di un registro a scorrimento controreazionato [952]   [952] Forse ho trovato dove si spiega come faccia un registro a scorrimento controreazionato a svolgere questo genere di compiti: penso che in una prossima edizione sarà interessante aggiungerlo., e lo stesso può essere usato anche per il calcolo della sindrome dal lato ricevente.

17.4.1.3 Codice BCH

Prende il nome dalle iniziali dei rispettivi inventori, e rappresenta una sottoclasse dei codici ciclici, in grado di correggere fino a t < n errori: per ottenere questo risultato occorre scegliere un numero di bit di protezione q ≤ mt in cui m ≥ 3 è un intero, una lunghezza delle codeword pari a n = 2m − 1, ed un polinomio generatore g(p) di grado massimo mt le cui radici sono potenze dell’elemento primitivo α del campo di Galois GF(2m) [953]   [953] http://en.wikipedia.org/wiki/BCH_code. In tal caso si ottiene dm ≥ 2t + 1, e la capacità di correggere fino a t errori. Nel caso in cui t = 1, si ricade nel caso dei codici di Hamming. La fase di correzione degli errori può essere realizzata mediante il calcolo di una sindrome, per mezzo di una matrice di controllo H realizzata a partire dalle potenze dell’elemento primitivo α, o sfruttando nuovamente proprietà algebriche, che eventualmente si traducono in soluzioni circuitali basate su registri a scorrimento controreazionati. Inoltre, è anche possibile applicare l’algoritmo iterativo di Berlekamp-Massey [954]   [954] http://en.wikipedia.org/wiki/Berlekamp-Massey_algorithm.

17.4.1.4 Codice di Reed-Solomon

Si tratta di un sottoinsieme dei codici bch, caratterizzato [955]   [955] http://en.wikipedia.org/wiki/Reed-Solomon_error_correction da parole di codice ad elementi non binari ma bensì L-ari, con L che deve essere una potenza prima [956]   [956] Ovvero deve essere della forma L = αk con α numero primo e k intero positivo. Ciò è necessario affinché gli L simboli corrispondano agli elementi di un campo di Galois GF(L).; scegliendo L = 2k ogni elemento (o simbolo) del codice corrisponde a k bit.
Un codice di Reed Solomon (N, K) produce codeword di N simboli L − ari ogni K simboli (ognuno di k bit) di informazione prelevati da m; esistono formulazioni
figure f_reed_solomon.png
in grado di produrre codebook sia di natura sistematica che non. La minima distanza del codice è pari a dm = N − K + 1, ed i metodi di decodifica (su cui non ci addentriamo [957]   [957] Ma si veda ad es. http://scienze-como.uninsubria.it/previtali/Bellini-TeoriaInfoCodiciNote.pdf) permettono di correggere fino a t = dm − 12 = N − K2 simboli L − ari per codeword; qualora la posizione dei simboli errati sia nota [958]   [958] Come nel caso dei codici a cancellazione, vedi ad es. https://en.wikipedia.org/wiki/Erasure_code può correggere il doppio dei simboli, ossia 2t. Dato che opera a livello di simbolo e non di singolo bit, non soffre del problema legato alle sequenze di errore come invece avviene per il codice di Hamming, almeno finché il numero di errori sul bit consecutivi non supera il valore t ⋅ k, ovvero non coinvolge più di t simboli.
Esempio Scegliendo k = 8, N = 2k − 1 = 255, t = 16 e K = N − 2t = 223 definiamo il codice RS(255, 223) che protegge K ⋅ k = 1784 bit inserendoli in codeword di N ⋅ k = 2040 bit, di cui 2t ⋅ k = 256 di ridondanza. Tale codice è in grado di correggere fino a 16 simboli ad 8 bit: qualora gli errori sul bit avvengano tutti in simboli differenti si ha il caso peggiore, in cui sono correggibili solamente 16 bit su 2040; viceversa nel caso migliore in cui gli errori sono consecutivi ed iniziano all’inizio di un simbolo, ne corregge fino a t ⋅ k = 128. Il tasso di codifica risulta Rc = K⁄N = 0.937.
Codice accorciato
Può accadere che i bit che costituiscono il flusso fb di dati da proteggere non sia omogeneo, ma presenti strutture sintattiche e quindi delimitazioni che si desidera riflettere nel flusso codificato [959]   [959] Come ad esempio avviene nella codifica di sorgenti multimediali (cap. 10); oppure, è il sistema di trasmissione ad imporre strutture di trama a dimensione fissa, e non si desidera frammentare una singola codeword a cavallo di time-slot differenti. In tali casi si omette la codifica (e la trasmissione) di alcuni dei K simboli di informazione, idealmente posti a zero, riducendo così la dimensione N della codeword pur mantenendo la stessa quantità di ridondanza N − K, accettando di ridurre il tasso di codifica Rc.
Esempio Il codice accorciato RS(204, 188) [960]   [960] Il valore di 188 byte deriva dalla dimensione di una cella atm (48 byte di dati e 5 di intestazione, § 23.2): infatti 48 ⋅ 4 = 192, ed una codeword si suddivide su 4 celle. viene ricavato dal RS(255, 239) (con 16 byte di ridondanza) ponendo a zero (e non trasmettendo) 51 dei 239 byte di informazione. Il tasso di codifica passa da 0.937 a 0.921.
In questi casi la codeword viene calcolata, in formato sistematico, a partire da una sequenza informativa fittizia che contiene anche i simboli posti a zero e poi non trasmessi; qualora in fase di decodifica questi risultino diversi da zero [961]   [961] Come osservato a pag. 1 in presenza di un numero di errori superiori al massimo correggibile, se ne verificano ancora di più., la codeword viene segnalata come errata agli stadi di elaborazione successivi.

17.4.1.5 Codifica concatenata

Come abbiamo fatto notare i codici Reed Solomon riescono a correggere efficacemente errori ripetuti, al contrario di quelli di Hamming, che invece hanno un buon comportamento in presenza di errori singoli. E dato che l’unione fa la forza, è possibile usarli assieme adottando lo schema mostrato in figura 17.15, in cui la prima codifica (di RS) è detta esterna perché più lontana dal canale, mentre per converso la seconda (di Hamming) è detta interna.
figure f_concatenati.png
Figure 17.15 Schema di codifica concatenata
Ad ogni simbolo di k bit della codeword esterna vengono aggiunti q bit di ridondanza
figure f_concatenati_2.png
da parte del codice interno, come mostrato a lato. Gli errori isolati introdotti da parte del canale sono corretti dal decodificatore interno, e se distanti tra loro per più di k + q bit, il codice esterno neanche si accorge di nulla; d’altra parte in assenza del codice interno, il solo codice di RS non sarebbe stato in grado di correggere più di N − K2 errori per codeword, qualora avvenuti ognuno in un simbolo diverso. Al contrario, in presenza di errori ravvicinati è il codice interno di Hamming a non poter fare nulla, anzi ne introduce di ulteriori, ma nello stesso simbolo: in tal caso il codice esterno di RS trova gli errori tutti concentrati in pochi simboli, e provvede alla loro correzione.
Codice prodotto
E’ un nome alternativo dato a questo schema di funzionamento [962]   [962] O meglio, ad una versione dello schema in cui la ridondanza interna viene calcolata sulla totalità dei simboli nella stessa posizione di M codeword esterne, come avviene per la tecnica esposta al § 15.6.3.2., e riflette il fatto che il tasso di codifica Rc complessivo è il prodotto dei tassi dei due stadi, dando luogo ad una velocità binaria in ingresso al canale pari a f’b = fbRic ⋅ Rec.
Interleaving
Qualora si manifestino sequenze di errore più lunghe di N − K2 ⋅ k bit, il numero di simboli del codice esterno che risultano errati diviene maggiore di quanto
figure f_concati_interl.png
esso non possa correggere, e lo schema precedente non funziona più. Per evitare questa situazione, tra i due stadi di codifica (e di decodifica) si frappone un blocco di interleaving (ed il suo inverso) (vedi § 15.6.2.3), come mostrato sopra.
La matrice di interleaving viene scritta per righe, inserendovi per intero M codeword del codice esterno, ed è letta per colonne dalla codifica interna, che vi aggiunge ulteriore ridondanza; dal lato ricevente la stessa matrice viene scritta per colonne con l’uscita della decodifica interna, e letta per righe da parte della decodifica esterna.
figure f_concati_interl_2.png
Le aree grigie in figura rappresentano una lunga sequenza di errore, che il codice interno non riesce a correggere: finché M (detto fattore di interleaving) è maggiore della più lunga sequenza di simboli errati previsti, questi ultimi vanno a finire in codeword (esterne) differenti, e possono dunque essere ancora corretti. Mentre in assenza di interleaver, i simboli errati sarebbero potuti finire tutti dentro la stessa codeword esterna.
Resta una ultima sventura possibile, ovvero la presenza di un disturbo periodico che si presenta alla stessa cadenza (o con un suo multiplo) con cui sono scritte le colonne da parte della decodifica interna. Ciò determina che tutti i simboli di una medesima codeword esterna siano errati, rendendone impossibile la correzione. Per rimediare anche a questa evenienza occorre adottare un metodo di interlevaing detto convoluzionale, il cui funzionamento non viene approfondito [963]   [963] Ma vedi ad es. https://en.wikipedia.org/wiki/Burst_error-correcting_code#Convolutional_interleaver, precisando solamente che quello discusso sopra è invece detto interleaver a blocco.

17.4.2 Codifica convoluzionale

A differenza della codifica a blocco, questa tecnica produce una sequenza binaria i cui valori dipendono da gruppi di bit di ingresso temporalmente sovrapposti, in analogia formale a quanto avviene con l’integrale di convoluzione, che calcola valori di uscita che dipendono da intervalli di quelli in ingresso, pesati dai valori della risposta
figure f17.40.png
impulsiva. Un generico codice convoluzionale è indicato con la notazione CC(n, k, K), che lo descrive come capace di generare gruppi di n bit di uscita (sequenza {x}) in base alla conoscenza di K simboli di ingresso (sequenza {m}), ognuno composto da k bit.
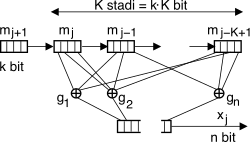
figure f4.41.png
Lo schema strutturale del codificatore, raffigurato a lato, ospita i K simboli della sequenza di ingresso (di k bit ciascuno) in un registro a scorrimento in cui per ogni nuovo simbolo mj che entra da sinistra, i precedenti scorrono a destra, ed il più “vecchio” viene dimenticato. Ognuno degli n bit di uscita xj(i), i = 1, 2, ..., n è calcolato eseguendo una somma modulo 2 tra alcuni dei k ⋅ K bit di ingresso, individuati da un vettore generatore gi (i = 1, 2, ..., n) costituito da una parola binaria di k ⋅ K bit, zero od uno a seconda se l’i-esimo sommatore modulo due sia connesso (o meno) al corrispondente bit della finestra di ingresso.
Il numero L = k ⋅ K di bit che contribuiscono al calcolo della parola di uscita viene indicato come lunghezza del vincolo, mentre la quantità ν = (K − 1) ⋅ k è indicata come memoria del codice per il motivo che vedremo presto. Resta poi valido il concetto di coding rate Rc = kn che rappresenta il rapporto tra quanti nuovi bit di informazione sono necessari in ingresso per ogni gruppo di n bit in uscita dal codificatore.
Automa e diagramma di transizione
Il numero di possibili configurazioni dei bit contenuti nello shift register è finito e pari a 2L = 2K ⋅ k. In base alla scelta degli n vettori gi, ad ogni configurazione corrisponde un unico valore dell’uscita, e ciò comporta che lo schema può essere descritto da una tabella della verità, ovvero da un automa a stati finiti, con annesso diagramma di transizione.
Osserviamo ora che il passaggio da uno stato all’altro non è qualsiasi, ma è stabilito dall’ultimo simbolo in ingresso mj, e pertanto il diagramma di transizione si costruisce individuando i 2ν stati S associati alle possibili combinazioni di bit dei precedenti K − 1 simboli di ingresso. Ad ogni stato competono 2k transizioni, una per ogni possibile mj di ingresso, diretta verso lo stato individuato dalla nuova configurazione di shift-register che si è determinata. Infine, ad ogni transizione è associato in modo univoco il gruppo di n bit xj(mj, Sj) da emettere in uscita [964]   [964] Lo stesso valore di xj potrebbe essere prodotto da più di una delle 2k ⋅ K diverse memorie del codificatore.. Ma prima che il discorso diventi troppo confuso, procediamo con un esempio pratico.
Codice CC(2,1,3)
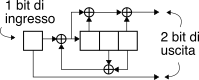
Consideriamo il codice convoluzionale il cui schema è mostrato in fig. 17.21-a), che produce due bit di uscita per ogni bit di ingresso in funzione degli ultimi tre, ovvero CC(n, k, K) = CC(2, 1, 3), caratterizzato da un tasso di codifica Rc = kn = 12, da una lunghezza del vincolo L = K ⋅ k = 3, una memoria ν = (K − 1) ⋅ k = 2 ed un numero di stati 2ν = 4, da ognuno dei quali si dipartono 2k = 2 transizioni. Se scegliamo come vettori generatori le parole [965]   [965] Il valore di un vettore generatore viene spesso espresso in notazione ottale, dunque nel nostro caso avremmo g1 = 78 e g2 = 58. g1 = (1 1 1) e g2 = (1 0 1) si ottiene la tabella della verità di fig. 17.21-b), che mostra i valori di uscita xj(i) ottenuti eseguendo gli xor descritti dai vettori gi sulla parola di tre bit costituita dall’ultimo ingresso mj e dai due precedenti ingressi, indicati come Sj, e che rappresentano appunto la memoria del passato all’istante j. Infine la fig. 17.21-c) rappresenta l’automa ed il diagramma di transizione corrispondente [966]   [966] In accordo allo schema https://it.wikipedia.org/wiki/Macchina_di_Mealy, in cui le transizioni tra stati sono disegnate con linee tratteggiate o continue a seconda se il valore mj dell’ultimo ingresso sia pari a zero o ad uno, e sono etichettate con la coppia di bit in uscita xj riportati nella tabella della verità.
a)     figure f4.42.png
   
   b)    
mj Sj xj(1) xj(2)
0 00 0 0
0 01 1 1
0 10 1 0
0 11 0 1
1 00 1 1
1 01 0 0
1 10 0 1
1 11 1 0
   
c)    figure f4.43.png
Figure 17.21 a) - architettura del codice convoluzionale CC(2, 1, 3); b) - tabella della verità; c) - diagramma di transizione; le linee tratteggiate indicano uno zero in ingresso
Come si può verificare, ogni stato ha solo due transizioni, e dunque per ogni ingresso sono possibili solo due valori dei quattro 4 che sarebbero possibili con due bit; inoltre questi valori differiscono in entrambi i bit [967]   [967] La dipendenza di xj da (mj, Sj) è legata alla scelta dei generatori gi. Nel caso in cui un valore xj(i) sia sempre uguale ad uno dei k bit di mj, il codice diviene sistematico..
Esempio Con una sequenza di ingresso {m} = {1010} si osserva che, seguendo il diagramma di transizione a partire dallo stato iniziale 00, la sequenza di stati risulta {S} = {00, 10, 01, 10, 01}, mentre quella di uscita è {x} = {11, 10, 00, 10}. E’ d’altra parte possibile anche il procedimento inverso, ossia conoscendo {x} e quindi {S} si può risalire ad {m}, sempre percorrendo le transizioni etichettate con i simboli xj. In definitiva, osserviamo come ad ogni coppia di sequenze ({m}, {x}) sia biunivocamente associata una sequenza di stati {S}.
Diagramma a traliccio
Per meglio visualizzare le possibili sequenze di stati si adotta una rappresentazione detta diagramma a traliccio (trellis) del codificatore, ottenuta a partire dalla riorganizzazione grafica del diagramma di transizione (fig. 17.21-c)) come mostrato a sin. in fig. 17.22-a). Il traliccio è quello al centro, costituito da nodi disposti su tante righe quanti sono gli stati dell’automa, e tante colonne quanti sono gli istanti temporali che vogliamo considerare. I collegamenti tra colonne del traliccio corrispondono alle transizioni dell’automa: ponendo uno stato iniziale Sj = 0 = 00, si costruisce la colonna j = 1 riportando le due possibili transizioni, tratteggiata o continua a seconda che sia entrato uno zero od un uno, e si etichettano le transizioni con la parola xj emessa in uscita. Il processo si ripete per tutti gli istanti temporali. In basso in figura è riportata una possibile sequenza codificata {x} trasmessa, in corrispondenza della quale l’effettivo percorso attraversato nel traliccio, e dunque la successione di stati {S} associata, è rappresentato dalle linee blu e più spesse.
figure f4.44.png
   
figure f4.45.png
Figure 17.22 a) - diagramma a traliccio e sequenza x trasmessa; b) - costi dH per la sequenza ricevuta; le linee tratteggiate indicano uno zero in ingresso

17.4.2.1 Criterio di decodifica

Come già osservato non tutte le sequenze di stati (e di uscite) sono ammissibili; indichiamo con X il loro insieme. Consideriamo quindi la sequenza {x̃} osservata all’uscita di un canale rumoroso, e contenente errori. In virtù dei vincoli, nel caso di errori sufficientemente isolati non esiste una sequenza di stati {S} in grado di produrre esattamente la sequenza ricevuta {x̃}, e la correzione degli errori consiste nel trovare la sequenza {Ŝ} ammissibile e tale che la corrispondente uscita {x̂} sia la più simile a {x̃}.
figure f4.47.png
La metrica adottata è la distanza di Hamming [968]   [968] Questo caso viene indicato con il termine hard-decision decoding in quanto il ricevitore ha già operato una decisione (quantizzazione) rispetto a x̃. Al contrario, se i valori ricevuti sono passati come sono al decodificatore di Viterbi, questo può correttamente valutare le probabilità p(x̃ ⁄ ^x) ed operare in modalità soft decoding, conseguendo prestazioni migliori. dH(^x, x̃) tra le due sequenze, ossia il numero di bit diversi tra le due, ed il criterio di decodifica viene definito come
(21.109) {x̂} =  argmin{x} ∈ X {dH(x, x̃)}
Decodifica di Viterbi
E’ il nome della tecnica basata sui principi della programmazione dinamica [969]   [969] Vedi as es. https://it.wikipedia.org/wiki/Programmazione_dinamica che permette di risolvere il problema (21.109) senza dover enumerare [970]   [970] Dato che da ogni stato si dipartono 2k archi, ad ogni istante j il numero di percorsi alternativi aumenta di un fattore 2k, crescendo molto velocemente all’aumentare di j. tutte le sequenze ammissibili {x} ∈ X.
A tale scopo gli archi del traliccio vengono etichettati come in fig. 17.22-b), con le dH(xj, x̃j) tra il simbolo xj associato alla transizione e quello x̃j ricevuto all’istante j. Per ogni particolare sequenza di stati {S} il costo dH(x, x̃) tra la sequenza ricevuta x̃ e quella x associata ad S è pari alla somma delle dH(xj, x̃j) che etichettano gli archi attraversati, ossia [971]   [971] Ad esempio, con riferimento alla fig. 17.22, la {S} = {00, 10, 11, 01, 10} ha un costo pari a 3.
(21.110)
dH(x, x̃) = ⎲⎳j dH(x(Sj ⁄ Sj − 1), x̃j)
Il criterio (21.109) è dunque equivalente a quello di trovare il percorso di minimo costo [972]   [972] Qualora la distanza tra x̃j ed un possibile xj sia invece espressa da una probabilità condizionata p(x̃j ⁄ xj), il processo di decodifica è detto di massima verosimiglianza e la decodifica è detta soffice (soft), vedi § 17.4.2.3. per l’attraversamento di un grafo valutato. Ciò avviene esaminando il traliccio per colonne da sinistra a destra, e valutando per ciascun nodo (riga) il miglior costo parziale [973]   [973] La scelta del miglior percorso parziale è l’applicazione del principio di programmazione dinamica, secondo il quale “quando due percorsi con costi diversi si incontrano in uno stesso nodo, quello di costo maggiore sicuramente non è la parte iniziale del percorso di minimo costo, e quindi può essere eliminato”. tra i diversi percorsi che lo raggiungono.
Esempio Applichiamo l’algoritmo descritto al caso in questione con l’aiuto della figura 17.24 (ottenuta a partire dalla 17.22-b)) che mostra sopra ad ogni nodo il risultato del calcolo del costo parziale del miglior percorso che lo raggiunge, ottenuto sommando i costi di attraversamento degli archi (fig. 17.22-b)) che lo compongono, mostrati in corsivo. Ad esempio, lo stato 00 all’istante j = 3 potrebbe essere raggiunto tramite il percorso tutto orizzontale che rimane nello stato 00, e che assomma un costo parziale di 4. A questo si preferisce il percorso proveniente dallo stato 01, che ha accumulato (per j = 2) un costo parziale di 1, a cui sommare dH(x(S00 ⁄ S01), x̃3) = dH(11, 00) = 2, per un nuovo costo parziale di 3.
All’estremità destra di figura 17.24 viene indicato il percorso di minimo costo, e la corrispondente dH(x, x̃) minima.
figure f4.46.png
Figure 17.24 Decodifica di Viterbi come percorso di minimo costo
In effetti l’algoritmo calcola solamente la dH minima, e per risalire alla sequenza di stati (e dunque di uscite) che l’ha prodotta, occorre (per ogni nodo del traliccio) memorizzare l’indice del nodo nella colonna precedente da cui parte l’arco che ha determinato il minor costo locale. Una volta individuato (all’ultima colonna) il nodo in cui termina il percorso di minor costo, svolgendo all’indietro la catena dei puntatori si trova la sequenza di stati {S} ottima (percorso verde a tratto spesso), e da questa in base alla fig. 17.22-a) sia la {m} che la {x̃}, che come si vede è quella esatta.
In fig. 17.25 è riportato un esempio di pseudo-codice che implementa l’algoritmo a partire da tre tabelle m(p, q), x(p, q) e A(p, q), di dimensione 2ν × 2ν, che contengono rispettivamente i valori di ingresso m e di uscita x in corrispondenza ad una transizione da p a q, ed un valore pari a 1 o 0 a seconda se la transizione esiste o meno. 
Tabelle:
  m(p, q)                       # ingresso m sull’arco da Sp a Sq
  x(p, q)                       # uscita x sull’arco da Sp a Sq
  A(p, q)                       # presenza di transizione da Sp a Sq
 

Inizializza:
per tutti gli stati p = 1, 2, ⋯2ν
  CJ(p) = 0
 

Iterazione:
per tutti gli istanti j = 1, 2, ⋯, J
  per tutti gli stati q = 1, 2, ⋯2ν
    CM(q) = CJ(q)             # miglior costo parziale al tempo j − 1
    CJ(q) = ∞                  # miglior costo fino a (q, j)
    per tutti gli stati p = 1, 2, ⋯, 2υ
      se A(p, q) =  = 1          # esiste transizione da p a q
        c = dH(x(p, q), x̃j) + CM(p)  # ipotesi da valutare
        se c < CJ(q)
          CJ(q) = c
          BP(q, j) = p          # backpointer al vincitore
 

Decodifica:
best = ∞
per tutti gli stati q = 1, 2, ⋯2ν
  se CJ(q) < best
    best = CJ(q)
    w = q                     # indice stato terminale
per tutti gli istanti j = J, ⋯, 2, 1
  p = BP(w, j)                 # miglior predecessore
  emette m(p, w)              # messaggio m scritto al contrario
  w = p
Figure 17.25 Pseudo codice dell’algoritmo di Viterbi
Il codice opera su di una sequenza di ingresso x̃ di J elementi, e ne produce una m di uguale lunghezza, ma temporalmente invertita. Ovviamente si possono pensare implementazioni molto più efficienti, ma l’esempio ha il solo scopo dimostrativo.
Considerazioni

17.4.2.2 Tail biting

Letteralmente traducibile come mordendo la coda, è un metodo per rendere un codice convoluzionale simile ad uno a blocchi. Il bitstream di ingresso viene suddiviso in segmenti di m bit, gli ultimi L dei quali sono utilizzati (in ordine inverso) per inizializzare lo shift-register del codificatore, che quindi inizia ad elaborare, uno alla volta e dall’inizio, i bit del segmento. Al suo termine, ovvero quando sarà entrato l’m − esimo bit del segmento, lo stato del codificatore sarà identico a quello con cui ha iniziato: ciò significa che se venisse di nuovo inserito lo stesso segmento (ovvero in forma periodica), si otterrebbe la stessa uscita, che può dunque essere riguardata nel suo insieme come la codeword associata al segmento.
Una variante della tecnica (detta zerotail), anziché inizializzare il codificatore ne azzera lo stato, ed aggiunge L bit pari a zero in coda al segmento, ottenendo lo stesso risultato, a spese di un peggioramento di Rc. Con la tecnica zerotail la decodifica sa che il percorso nel traliccio deve iniziare e terminare con lo stato nullo, e dunque al termine della digestione della codeword associata al segmento si può iniziare il backtraking dei puntatori da li, oppure segnalare la presenza di eccessivi errori, qualora non sia quello il percorso di minimo costo.
Con l’inizializzazione dello stato, invece, il traliccio diviene periodico (alcuni lo definiscono circolare), e l’algoritmo di Viterbi viene fatto lavorare su di una periodizzazione della codeword ricevuta; dopo alcuni periodi si individua lo stato di minimo costo, e recuperati i puntatori (per un periodo-codeword) a partire da quello.

17.4.2.3 Decodifica a decisione soffice

Fino ad ora la decodifica di canale è stata applicata a valle del processo di decisione [974]   [974] Per questo detta hard decision decoding in quanto opera su decisioni già prese., in modo da individuare le codeword come quelle con la minima distanza di Hamming rispetto al risultato prodotto dal decisore. Se invece la decodifica di linea non esegue nessuna decisione, ma inoltra interi blocchi di n campioni y = (y1, y2, ⋯, yn) prelevati dal segnale ricevuto, la decodifica di canale può individuare le codeword trasmesse come quelle con la minima distanza euclidea dE rispetto a quanto ricevuto [975]   [975] Tale possibilità è indicata come soft in quanto richiede operazioni in virgola mobile; si veda ad es. la spiegazione fornita presso
http://www.gaussianwaves.com/2009/12/hard-and-soft-decision-decoding-2/., ottenendo prestazioni migliori a spese di un maggior onere di calcolo. Questa tecnica valuta la distanza come
(21.111) dE(y, xi) = ⎲⎳nj = 1(yj − xij)2
tra i valori (continui) yj ricevuti e quelli (binari) che si sarebbero dovuti ricevere nell’ipotesi che fosse stata trasmessa la i − esima delle possibili codeword xi = (xi1, xi2, ⋯, xin), decidendo quindi per la codeword x̂ che rende dE(y, x̂) minima.
Decodifica di massima verosimiglianza
Di fatto minimizzare la distanza (21.111) equivale a massimizzare la verosimiglianza logaritmica ln (pn(y ⁄ xi)) dell’ipotesi che sia stata trasmessa la codeword xi avendo ricevuto la v.a. n − dimensionale y affetta da rumore gaussiano n di varianza σ2. Infatti considerando i bit incorrelati [976]   [976] Anche se la codifica introduce correlazione, l’ipotesi è troppo comoda per poter arrivare al risultato!, pn(y ⁄ xi) è pari al prodotto delle pn(yj ⁄ xij) dei singoli bit, e ln (pn(y ⁄ xi)) diviene una somma, i cui termini [977]   [977] Vedere come si è proceduto a pag. 1.
(21.112)
ln (pn(yj ⁄ xij)) = − ln (√2πσ) − (yj − xij)22σ2
sono legati a quelli (cambiati di segno) che compaiono nella (21.111), dato che ne il primo termine di (21.112) ne il denominatore del secondo intervengono nella minimizzazione di (21.111).
Mentre per un codice a blocchi appare problematico valutare la (21.111) per tutte le possibili xi, le considerazioni ora svolte sono invece particolarmente adatte al contesto della codifica convoluzionale, dato che basta sostituire nella (21.110) la dH con la dE per il calcolo dei costi associati ai percorsi nel traliccio esplorato dall’algoritmo di Viterbi. In tal caso si assiste ad un miglioramento di prestazioni (rispetto all’approccio hard) equivalente ad un aumento di Eb⁄N0 di circa 2 dB.
Prestazioni
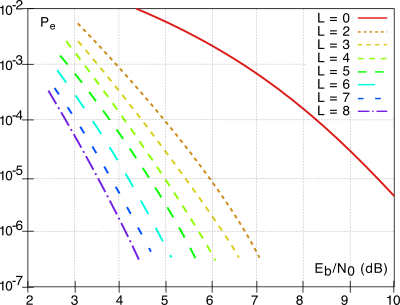
La figura che segue riporta i valori della Pbite residua
figure f4.prest-vit.png
per la decodifica di Viterbi di un CC con Rc = 1⁄2 al variare della lunghezza del vincolo L, il cui bitstream viene trasmesso mediante modulazione qpsk, in funzione del rapporto Eb⁄N0 in ricezione. Osserviamo il conseguimento di un guadagno di codifica (pag. 1) che per una Pe = 10 − 5 va da circa 3.5 a 6 dB per le diverse scelte di L, che corrispondono a tralicci da 4 a 256 stati.
Oppure, visto nell’altro senso, per un Eb⁄N0 di 5 dB otteniamo una Pe migliore tra 100 e più di 10000 volte rispetto al caso non codificato.

17.4.2.4 Altri schemi di codifica convoluzionale

Lo schema riportato nell’esempio di fig. 17.21 non è l’unico possibile. Anche se permette di variare il tasso di codifica Rc = kn variando i valori di k ed n, questi impattano anche su complessità del traliccio, lunghezza del vincolo L e distanza libera dm; per
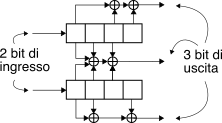
figure f4.42-doppio.png
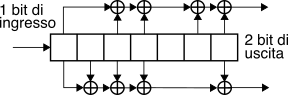
garantirsi la massima libertà di azione sui parametri della codifica, sono state definite anche architetture differenti. Lo schema riportato a lato ad esempio dispone i k = 2 bit di ingresso su due diversi rami, ed impiegando tre generatori, consegue un tasso Rc = kn = 23 con 64 stati, K = 8 ed L = 8.
Anche se non è stata affrontata la parte di teoria che descrive i CC in termini di risposta impulsiva e risposta in frequenza, non può sfuggire la similitudine tra le architetture illustrate e quelle dei filtri fir, pur se in logica modulo due. Ma esiste anche la possibilità di realizzare un CC ricorsivo, in cui cioè sono presenti operazioni xor
figure f4.42-recur.png
all’indietro e non solo in avanti, come nello schema mostrato in figura [978]   [978] In particolare, lo schema illustrato viene impiegato nella telefonia lte (ETSI TS 136 212) nell’ambito della codifica turbo, vedi § 17.5.1. che consegue Rc = 1⁄2, e che è anche sistematico in quanto un bit di uscita su due replica quello di ingresso.

17.4.2.5 Codice perforato

Modificare completamente l’architettura del codificatore non sembra la scelta migliore per poter variare Rc, dato che ciò comporta la totale modifica del traliccio su cui è basata la decodifica. Una diversa opzione è quella di omettere del tutto la trasmissione di alcuni dei bit presenti nella sequenza codificata, operazione nota come perforazione (puncturing) del codice: ad esempio eliminare un bit ogni tre dall’uscita di un CC con Rc = 1⁄2 determina un nuovo Rc = 3⁄4, dato che servono ora tre bit di ingresso per produrne quatto di uscita, anziché sei. Ovviamente in questo
figure f4.punturato.png
caso le capacità correttive peggiorano, ma il processo di decodifica può aver luogo comunque dato che il ricevitore conosce le posizioni non trasmesse, e per esse considera una distanza neutra pari a 0.5, come esemplificato alla tabella a lato, dove con δi si indica la distanza (hard o soft) tra l’i − esimo bit nella sequenza ricostruita, e le corrispondenti ipotesi espresse dal traliccio.
La percentuale di perforatura può essere resa variabile nel corso della trasmissione in funzione del tasso di errore rilevato, in modo da ridurre la ridondanza nel caso di una buona qualità di ricezione, o mantenerla elevata in caso di peggioramento.
Esempio Lo standard di trasmissione dvb utilizza il CC con due generatori mostrato in figura, con 64 stati, vincolo di lunghezza L=7, dm = 10 e Rc = 1⁄2. Le uscite di entrambi i rami possono essere perforate in accordo allo schema in tabella, che mostra anche la variazione del tasso di codifica e della distanza minima: la posizione degli zeri nella matrice di perforazione indica i bit di cui è omessa la trasmissione.
figure f4.42-DVB.png
   
Rc 1⁄2 2⁄3 3⁄4 5⁄6 7⁄8
matrice di 1 10 101 10101 1000101
perforazione 1 11 110 11010 1111010
dm 10 6 5 4 3

17.4.2.6 Concatenazione Solomon-Viterbi

La strategia illustrata al § 17.4.1.5 di collegare in cascata un codice esterno in grado di correggere errori a pacchetto (come il Reed-Solomon) con uno interno particolarmente idoneo a correggere errori isolati viene impiegata con vantaggio utilizzando come secondo un codice convoluzionale, che come abbiamo illustrato produce errori a pacchetto qualora si eccedano le sue capacità correttive.
E’ precisamente la soluzione adottata per la codifica del segnale dvb [979]   [979] Vedi le specifiche ufficiali presso
https://www.etsi.org/deliver/etsi_en/300400_300499/300421/01.01.02_60/en_300421v010102p.pdf, in cui il CC dell’esempio precedente è affiancato (tramite un interleaver convoluzionale di profondità 12) da un codice RS accorciato (214, 188) derivato dal (255, 239) (pag. 1) che, con la sua capacità di poter correggere 8 simboli per codeword, porta il tasso di errore residuo ad una Pe di 10 − 11 pur in presenza di un Eb⁄N0 di 3.2 dB.
figure f4.solomon-viterbi.png

17.4.2.7 Viterbi con uscite soffici

Quando la decodifica di canale viene fattorizzata su due blocchi in cascata diviene globalmente vantaggioso che il primo dei due possa alimentare il secondo con valori continui, in modo da esprimere l’affidabilità della decisione presa.
Al § 17.4.2.3 abbiamo notato come l’algoritmo di Viterbi alimentato con ingressi soffici di n campioni y = (y1, y2, ⋯, yn) pervenga ad una decisione di massima verosimiglianza a riguardo di una codeword x̂ ovvero tale che x̂ = argmaxx p(y ⁄ x), da cui risalire al messaggio m̂ = (m1, m2, ⋯, mk) associato alla codeword x̂. Analizziamo ora una sua variante capace di produrre anche una probabilità a posteriori p(mj ⁄ y) per ognuno dei bit mj j = 1, 2⋯, k decodificati, o quantomeno una misura di affidabilità della decisione. Tale variante è denominata SOVA [980]   [980] Illustrato per esteso in J.Hagenauer, P.Hoeher, A Viterbi algorithm with soft-decision outputs and its applications, 1989 ieee, a cui si ispira questa parte, e reperibile ad es. presso
http://shannon.ece.ufl.edu/eel6550/lit/SOVA.pdf (soft output Viterbi algorithm), ed in associazione ad un ingresso soffice, realizza una decodifica detta SISO (soft input, soft output).
L’uscita soffice si ottiene associando ad ogni mj = ± 1 decodificato anche un valore pj che misura la probabilità che la decisione sia errata, in modo che l’affidabilità possa essere espressa come
(21.113) Lj = ln 1 − pjpj ≥ 0
e l’uscita soffice come Λj = mjLj in cui il segno è la decisione hard, e la verosimiglianza logaritmica (21.113) ne esprime il modulo. Vediamo quindi come determinare pj.
Valutazione della prob. di decisione errata
Adottiamo per semplicità un CC sui cui nodi del traliccio convergono due sole transizioni, e prendiamo in considerazione un istante i in cui per ognuno dei 2ν stati [981]   [981] Si è volutamente mantenuta la notazione introdotta al § 17.4.2. si occorre scegliere tra due ipotesi di percorso parziale, che indicizziamo con h = 1, 2. Indicando con δ un istante del passato per il quale tutti i 2ν percorsi superstiti condividono con elevata probabilità un medesimo progenitore (vedi fig. 17.30)
figure f4.SOVA.png
Figure 17.30 Traliccio con cui illustrare il funzionamento di sova.
Due percorsi convergono su uno stesso stato si,
e le sequenze informative associate differiscono in due istanti
la decisione all’istante i avviene confrontando i costi parziali
(21.114)
Ch = ⎲⎳ij = i − δ dE(yj, x(h)j)         h = 1, 2
in cui yj è la parola (soft) di n bit ricevuta all’istante j ed x(h)j è la parola (con valori ±1) emessa allo stesso istante dal codice in corrispondenza del h−esimo percorso. Ricordando quanto discusso al § 17.4.2.3, la (21.114) è legata in modo diretto alla verosimiglianza logaritmica − ln (p(y ⁄ x(h))) delle ipotesi x(h) avendo osservato y; pertanto è lecito assumere che
Prob{percorso h} ≈ e − Ch      h = 1, 2
indicando con  ≈  una qualunque relazione monotona crescente. Assumendo ora h = 1 l’indice del miglior percorso e h = 2 di quello scartato (e dunque C1 < C2), la probabilità di aver scelto il percorso sbagliato è pari a
(21.115)
psi = e− C2e− C1 + e− C2 = 11 + eC2 − C1 = 11 + eΔ
con Δ = C2 − C1 ≥ 0. Dunque psi è pari a 0.5 quando C2 = C1 mentre tende a zero qualora C2 ≫ C1; in altre parole quanto più i due costi sono simili, tanto più la decisione potrebbe essere errata.
La misura di affidabilità (21.115) ci avverte che, qualora la decisione sia errata, allora (con probabilità psi) sono errate anche le decisioni nei q istanti in cui i bit di informazione m nei due percorsi differiscono, ossia
(21.116) m(1)j ≠ m(2)j         j = j1, ⋯, jq
evidenziati in fig. 17.30 da un differente tratteggio, mentre gli istanti j in cui m(1)j = m(2)j non sono danneggiati dalla decisione errata. Se abbiamo preventivamente salvato le prob. di errore p̂j per gli indici espressi dalla (21.116), queste vengono aggiornate come
(21.117)
p̂j = p̂j(1 − psi) + (1 − p̂j)psi         j = j1, ⋯, jq
ovvero rimangono uguali con prob. 1 − psi, o si aggiornano al nuovo valore psi con prob. 1 − p̂j di non aver sbagliato all’istante j.
Differenze rispetto a Viterbi classico
In sostanza l’algoritmo ricalca quello in § 17.4.2.1 e produce le medesime decisioni hard, ma ognuna corredata dalla verosimiglianza logaritmica Lj = ln 1 − p̂jp̂j calcolata a partire dai valori ottenuti tramite la (21.117). Per arrivare a questo risultato occorre memorizzare per ogni istante e per ogni stato, oltre al puntatore al miglior predecessore, anche le differenze Δ tra i costi, da cui ottenere i valori p̂j (eqq. (21.115) - (21.117)) e Lj (21.113) in fase di decodifica.
Applicazioni
Il metodo esposto trova impiego nella demodulazione di segnali con memoria come la modulazione a traliccio e cpm (§ 16.10), nella equalizzazione di canali con memoria (§ 18.4.5), e come stadio di decodifica interno di una codifica concatenata (§§ 17.4.1.5 e 17.4.2.6). Quest’ultimo caso si presta particolarmente bene all’utilizzo di una tecnica convoluzionale anche per il codice esterno, operante ovviamente in modalità soft, e separato da quello interno da un adeguato stadio di interleaving. Lo stadio esterno potrà quindi eseguire eseguire una decodifica di massima verosimiglianza a partire dalla sequenza Λj = m̂jLj (m̂j = ±1, Lj ≥ 0) proveniente dallo stadio sova interno, decidendo per il messaggio mdec tale che
(21.118) mdec =  argmaxm {⎲⎳j mjΛj}
Mentre il caso di un codice esterno a blocchi non permette di risolvere agevolmente la (21.118), consideriamo il caso di un semplice controllo di parità a bit singolo (§ 15.6.3.1), e poniamoci nella condizione che lo stesso rilevi la presenza di un bit errato. Anziché invocare una ritrasmissione, può procedere modificando la decisione per il bit a cui corrisponde la massima probabilità di errore, ovvero a cui corrisponde il valore Lj più piccolo.
 Sezione 17.3: Capacità di canale continuo Su Capitolo 17: Capacità e codifica di canale Sezione 17.5: Verso il limite di Shannon