Sezione 2.1: Prerequisiti trigonometrici Su Capitolo 2: Serie di Fourier e spazio dei segnali Sezione 2.3: Teorema di Parseval 

2.2 Serie di Fourier

Come anticipato a pag. 1, un segnale x(t) periodico è un segnale di potenza, reale o complesso, che assume ripetutamente gli stessi valori a distanza multipla di un
figure f2.1.2.png
intervallo temporale T denominato periodo, ovvero tale che
x(t) = x(t + T) ∀t
L’inverso di T è detto frequenza fondamentale F = 1T o prima armonica [58]   [58] Da un punto di vista etimologico, la serie armonica è definita come ∑∞n = 11⁄n, mentre gli armonici di
figure Harmonic_partials_on_strings.png
una corda di chitarra sono i suoni prodotti dopo averne bloccato la vibrazione in corrispondenza di 1⁄n − esimo della sua lunghezza. Dal punto di vista della teoria musicale le armoniche di una nota sono altre note a frequenza multipla della prima. In particolare la seconda armonica corrisponde ad un intervallo di ottava, mentre la quarta a due ottave. E la terza armonica? Partendo ad esempio dal la4, e sapendo che ogni semitono della scala temperata corrisponde ad un rapporto di frequenze pari a 21⁄12 rispetto al semitono precedente, determiniamo il numero di semitoni Ns tra il la4 e la sua la terza armonica. Ad un rapporto di frequenze pari a 2Ns⁄12 = 3 corrisponde Ns12 = log23 ≃ 1.5849 e quindi Ns = 19 semitoni, ovvero un intervallo di dodicesima, cioè il mi5 che viene dopo il la5 dell’ottava successiva. Procedendo allo stesso modo si trova che la quinta, sesta e settima armonica corrispondono rispettivamente a do#6, mi6 e sol6: pertanto, con le prime sette armoniche si compone un accordo di settima di dominante. di x(t), espressa in Hertz, dimensionalmente pari all’inverso di un tempo [sec− 1].
Per i segnali periodici esiste una forma di rappresentazione basata sulla conoscenza di una serie infinita di valori complessi {Xn} denominati coefficienti di Fourier, calcolati a partire da un periodo di segnale come
(10.6) Xn = 1T T⁄2⌠⌡ − T⁄2x(t) e −j2πnFtdt
e che permettono [59]   [59] Per una discussione relativa alla convergenza della serie (10.7) si veda il § 2.5.1. la ricostruzione di x(t) nella forma di una combinazione lineare di infinite funzioni esponenziali complesse e j2πnFt, mediante l’espressione nota come serie di Fourier:
(10.7) x(t) = ∞⎲⎳n = −∞Xn e j2πnFt
Osserviamo che:

2.2.1 Serie di Fourier per segnali reali

Qualora il segnale periodico x(t) di cui si calcola la serie di Fourier sia reale, si verificano le importanti conseguenze che ora analizziamo.

2.2.1.1 Simmetria coniugata o Hermitiana

Quando x(t) è reale i relativi coefficienti di Fourier godono della importante proprietà di simmetria coniugata, che consiste nell’eguaglianza
(10.8) Xn = X *  − n
ovvero il coefficiente con indice n è il complesso coniugato di quello con indice  − n, avendo uguale parte reale e parte immaginaria di segno opposto. Infatti scomponendo l’esponenziale complesso e −j2πnFt mediante la (10.3) come cos2πnFt − jsin2πnFt, ed essendo x(t) reale, l’integrale (10.6) si suddivide in due integrali entrambi reali
(10.9)
Xn = 1T T⁄2⌠⌡ − T⁄2x(t)cos(2πnFt)dt − j 1T T⁄2⌠⌡ − T⁄2x(t)sin(2πnFt)dt
relativi al calcolo rispettivamente della parte reale e di quella immaginaria di Xn, ovvero ℜ{Xn} = 1T ∫T⁄2 − T⁄2x(t)cos(2πnFt)dt e ℑ{Xn} = 1T ∫T⁄2 − T⁄2x(t)sin(2πnFt)dt. Essendo il coseno una funzione pari, ℜ{Xn} ha lo stesso valore indipendentemente dal segno di n, mentre ℑ{Xn} cambia segno con n, essendo il seno una funzione dispari. Ciò comporta una proprietà analoga anche per modulo e fase di Xn, e quindi in definitiva
x(t)  reale   ⇔   ⎧⎨⎩ ℜ{Xn} = ℜ{X − n}   ℑ{Xn} = − ℑ{X − n}    e    ⎧⎨⎩ |Xn| = |X − n|   arg{Xn} = − arg{X − n}
riassumibile nella frase
se x(t) è reale i coefficienti Xn hanno parte reale pari e parte immaginaria dispari, ovvero modulo pari e fase dispari
da cui discende anche [61]   [61] Notiamo infatti che se x(t) è (reale) pari, allora il termine x(t)sin2πnFtdt che compare nel secondo temine della (10.9) è dispari, ed il suo integrale esteso ad un intervallo simmetrico rispetto all’origine è nullo, e pertanto ℑ{Xn} = 0. Se invece x(t) è (reale) dispari, allora è x(t)cos2πnFtdt nel primo termine ad essere dispari, e dunque per lo stesso motivo si annulla l’integrale che esprime ℜ{Xn} = 0.
se x(t) oltre ad essere reale è anche pari, i coefficienti Xn sono reali (pari), mentre se x(t) è reale dispari, gli Xn sono immaginari (dispari).

2.2.1.2 Interpretazione dei coefficienti di Fourier come fasori

Confrontando la formula di ricostruzione (10.7) con la (10.5) ricavata al § 2.1.3 per il caso di un x(t) cosinusoidale, e tenendo conto della proprietà di simmetria coniugata (10.8),
figure f2.1.1b.png
Figure 2.10 Somma vettoriale di fasori armonici per t0 e t1
è possibile pensare un segnale periodico reale come la parte reale del risultato di una somma vettoriale di un insieme infinito di fasori Xn (di modulo doppio di quello dei coefficienti Xn), ognuno rotante con una velocità angolare ωn = 2πnF multipla della fondamentale 2πF.
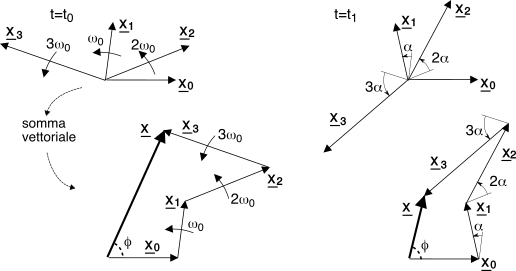
La figura 2.10 mostra [62]   [62] Se la figura non appare del tutto chiara, non hai tutti i torti. Prova allora a dare una occhiata a queste animazioni https://www.animations.physics.unsw.edu.au/jw/phasor-addition.html, https://en.wikipedia.org/wiki/File:Fourier_series_sawtooth_wave_circles_animation.gif e https://en.wikipedia.org/wiki/File:Fourier_series_square_wave_circles_animation.gif la somma vettoriale dei primi tre termini Xn e j2πnFt della (10.7) per n ≥ 0, valutata per due istanti di tempo consecutivi t0 e t1 > t0, ed evidenzia come nell’intervallo τ = t1 − t0 i fasori X2 e X3 siano ruotati di un angolo nα multiplo di quello α = 2πFτ di cui ha ruotato X1.
Esercizio  Calcoliamo i coefficienti dello sviluppo in serie di Fourier per il segnale x(t) = Acos(2πFt + φ). Esprimiamo innanzitutto l’integrale che fornisce i coefficienti nei termini della formula di Eulero per il coseno:
Xn  =  AT T⁄2⌠⌡ − T⁄2 e j2πFte jφ + e −j2πFte −jφ2 e −j2πnFtdt        =  A2T ( e jφT⁄2⌠⌡ − T⁄2 e j2πFt e −j2πnFtdt + e −jφT⁄2⌠⌡ − T⁄2 e −j2πFt e −j2πnFtdt )
in cui F = 1T, e consideriamo la funzione integranda e±j2πFt e −j2πnFt per i diversi valori di n:

2.2.1.3 Serie trigonometrica

Qualora i coefficienti Xn presentino simmetria coniugata la (10.7) può essere riscritta [63]   [63] Infatti X±n = Mne±jφn e dunque il termine entro parentesi graffe risulta pari a
Mn(e j(2πnFt + φn) + e −j(2πnFt + φn)) = Mn2cos(2πnFt + φn) come
(10.10)
x(t) = X0 +∞⎲⎳n = 1{Xn e j2πnFt + X − n e −j2πnFt} = M0 + 2∞⎲⎳n = 1Mncos(2πnFt + φn)
ovvero in forma di una serie di coseni; notiamo che X0 = M0 è necessariamente reale, in quanto la fase deve risultare una funzione dispari della frequenza. Similmente, le proprietà relative alle parti reale ed immaginaria degli Xn permettono di scrivere [64]   [64] In questo caso in virtù dell’uguaglianza j2 = − 1 il termine tra parentesi graffe diviene
Rncos(2πnFt) + jRnsin(2πnFt) + jIncos(2πnFt) − Insin(2πnFt)  +      Rncos(2πnFt) − jRnsin(2πnFt) − jIncos(2πnFt) − Insin(2πnFt)
che si semplifica nel risultato mostrato.
x(t)  = X0 + ∞⎲⎳n = 1{(Rn + jIn) e j2πnFt + (Rn − jIn) e −j2πnFt} =   = R0 + ∞⎲⎳n = 1{2Rncos(2πnFt) − 2Insin(2πnFt)}
in cui R0 = M0 = 1T ∫T⁄2 − T⁄2x(t)dt e
⎧⎨⎩ Rn = ℜ{xn} = 1T ∫T⁄2 − T⁄2x(t) cos(2πnFt)dt In = ℑ{xn} = 1T ∫T⁄2 − T⁄2x(t) sin(2πnFt)dt
Pertanto nel caso in cui x(t) sia un segnale reale la serie di Fourier può essere ricondotta ad uno sviluppo in termini di funzioni trigonometriche, ed in particolare ad una serie di soli coseni (con fase nulla) nel caso in cui x(t) sia pari, oppure una serie di soli seni (sempre con fase nulla), nel caso in cui sia dispari.

2.2.1.4 Serie di Fourier di un’onda rettangolare

Applichiamo quanto fin qui discusso ad un particolare segnale periodico, realizzato ripetendo con periodo T un impulso rettangolare (pag. 1) di base τ < T,
figure f2.2.png
ottenendo il risultato mostrato a lato per un valore di duty cycle [65]   [65] Il termine duty cycle si traduce ciclo di impegno, ed è definito come il rapporto percentuale tra il tempo per cui l’onda quadra è diversa da zero, ossia duty cycle  = τT*100 %. del 33%, la cui espressione analitica può essere scritta
x(t) = A∞⎲⎳n = −∞ rectτ(t − nT)
in cui si è adottata la notazione rectτ(t) per rappresentare l’impulso, mentre l’argomento (t − nT) indica una traslazione temporale di ciascun rettangolo a destra (vedi § 1.5.2) [66]   [66] Oppure a sinistra, qualora n sia negativo e quindi  − nT positivo. (ossia verso i valori positivi di t) di nT istanti, cosicché la sommatoria rappresenta appunto la replica dello stesso impulso rettangolare infinite volte in avanti ed all’indietro.
Il calcolo dei coefficienti di Fourier per il segnale in questione non presenta particolari difficoltà, ma l’esito si presta a considerazioni interessanti. Applicando un risultato noto [67]   [67] Sappiamo infatti che ∂∂xef(x) = ef(x) ⋅ ∂f(x)∂x, e quindi ∫baef(x)dx = 1⁄∂f(x)∂x ⋅ ef(x)|ba, si ottiene
(10.11)
Xn  =  1T T⁄2⌠⌡ − T⁄2x(t)e −j2πnFtdt = 1T τ⁄2⌠⌡ − τ⁄2Ae −j2πnFtdt =   =  A 1T e −j2πnFt − j2πnF||τ⁄2 − τ⁄2 = A 1T τπnFτ e j2πnFτ2 − e −j2πnFτ22j =      =  A τT  sin(πnFτ)πnFτ = A τT sinc(nFτ)
in cui nella seconda uguaglianza gli estremi di integrazione sono stati ristretti all’intervallo di effettiva esistenza del segnale, mentre la penultima eguaglianza si giustifica ricordando le formule di Eulero.
Il risultato (10.11) ottenuto mostra come i coefficienti Xn della serie di Fourier per l’onda rettangolare dipendano dai valori di sin(πnFτ)πnFτ calcolati per n intero; tale espressione viene però rappresentata nei termini della funzione seno cardinale (vedi pag. 1)
(10.12) sinc(x) = sin(πx)πx
che ricorre spesso nel testo, che è raffigurata nella parte sinistra di fig. 2.12, e che passa da zero per valori interi dell’argomento x, tranne che per x = 0, dove vale uno.
figure f2.3.png
Figure 2.12 Funzione sinc(x) e coefficienti di Fourier dell’onda quadra
Nella parte centrale di fig. 2.12 è mostrato l’andamento degli Xn che, qualora si ponga τ = T3 (corrispondente al duty cycle del 33%) e ricordando che F = 1⁄T, valgono Xn = A3  sinc(n⁄3), producendo dunque valori di Xn nulli in corrispondenza degli indici n = 3, 6, 9, ....
La parte destra di fig. 2.12 mostra ancora il valore dei coefficienti Xn, ma lungo una scala in Hertz, dato che il coefficiente Xn di indice n individua l’ampiezza della componente a frequenza nF = nT relativa all’n − esima armonica, che per τ = T3 è pari ad nF = nT = n3τ Hz: quindi i valori di n per cui gli Xn si annullano corrispondono alle frequenze 1⁄τ, 2⁄τ, 3⁄τ... e dipendono dalla durata τ del singolo impulso, mentre la spaziatura tra le armoniche è pari ad F = 1T e dipende esclusivamente dal periodo della forma d’onda. A partire da tali considerazioni, valutiamo come si modificano i coefficienti Xn al variare di τ e di T.
Relazione tra i coefficienti della serie ed i parametri dell’onda quadra
La parte in alto di fig. 2.13 mostra quattro possibili modi di variare l’onda quadra di partenza: la colonna di sinistra rappresenta il caso in cui il periodo T si mantenga costante, mentre la durata τ della fase attiva di ogni ciclo raddoppia (prima riga) o si dimezza (terza riga), mentre la colonna di destra considera il caso in cui τ si mantiene invariato, mentre il periodo T si dimezza o raddoppia in modo da ottenere lo stesso duty cycle τT di sinistra, ovvero pari al 66% (prima riga), 33% (al centro) o 12,5% (terza riga).
figure f2.2a.png
figure f2.2b.png



figure f2.4.png
figure f2.5.png
Figure 2.13 Modifiche allo spettro di ampiezza per variazioni della forma d’onda
La parte inferiore di Fig. 2.13 mostra le corrispondenti variazioni per i valori dei coefficienti dello sviluppo in serie, calcolate facendo uso della (10.11), e raffigurati su di una scala in Hertz. Sul lato sinistro (caso del periodo costante) osserviamo che le armoniche mantengono la stessa spaziatura 1T, ma l’inviluppo sinc(nFτ) si contrae ed espande rispettivamente. Il lato destro della figura (caso di τ costante) mostra come sia l’inviluppo degli Xn a rimanere costante, mentre le armoniche si diradano (sopra) ed infittiscono (sotto) rispettivamente all’aumentare ed al diminuire del periodo. Infine, notiamo come al diminuire del duty cycle si assista in entrambi i casi ad una riduzione dell’ampiezza degli Xn, legata alla riduzione di potenza del segnale (vedi sezione 2.3).

2.2.2 Serie di Fourier troncata

Come affermato al § 2.2, la serie di Fourier x(t) = ∑∞n = −∞Xn e j2πnFt permette di riottenere esattamente il segnale x(t) a partire da tutti i valori Xn; analizziamo ora cosa accade qualora la sommatoria sia invece troncata, ossia limitata ai 2N + 1 termini centrati attorno ad n = 0, utilizzando cioè solamente i coefficienti Xn con indice  − N ≤ n ≤ N. A tal fine, consideriamo un’onda quadra con duty-cycle del 50%
x(t) = ∞⎲⎳k = −∞ rectT⁄2(t − kT)
per la quale al § 2.2.1.4 abbiamo ottenuto l’espressione Xn = τT sinc(nFτ) per i relativi coefficienti di Fourier, che per τ = T2 fornisce Xn = 12 sinc⎛⎝n2⎞⎠, diverso da zero solo con n dispari [68]   [68] Si può mostrare che le armoniche pari risultano nulle per tutti i segnali periodici alternativi, ovvero per i quali (a parte una eventuale componente continua) un semiperiodo eguaglia l’altro, cambiato di segno.. Dalla relazione (10.12) otteniamo che 12 sinc⎛⎝n2⎞⎠ = sin π2n ⁄ πn, e possiamo dunque esprimere i coefficienti di Fourier dell’onda quadra come
X0 = 12  ;      Xn = ⎧⎨⎩ ( − 1)n − 12πn    con n dispari 0     con n pari
figure f2.8b.png
Essendo inoltre x(t) reale pari, sappiamo che x(t) può essere espresso come serie di coseni
x(t) = X0 + ∑∞n = 12Xncos(2πnFt)
che si presta ad essere facilmente calcolato numericamente e graficato arrestando ad N lo sviluppo in serie
^xN(t) = X0 + ∑Nn = 12Xncos(2πnFt)
producendo il risultato mostrato in figura per diverse scelte di N.
Come era da aspettarsi al crescere di N la ricostruzione è sempre più accurata, tranne che per le oscillazioni in prossimità della discontinuità, che prendono il nome di fenomeno di Gibbs [69]   [69] Vedi https://it.wikipedia.org/wiki/Fenomeno_di_Gibbs. Da un punto di vista informale, accade che l’assenza delle componenti armoniche a frequenza f = nF più elevata fa si che l’errore si localizzi in prossimità degli istanti in cui x(t) varia più velocemente. Da un punto di vista pratico, il caso studiato è un esempio di cosa può succedere quando un segnale viene privato delle sue componenti a frequenza più elevata, come ad esempio a seguito di un filtraggio passa-basso. Da un punto di vista analitico, si dimostra che l’errore eN(t) = x(t) − ^xN(t) ha media quadratica 1T ∫ e2(t)dt minima, e risulta ortogonale (vedi § 2.4) a ^xN(t).
 Sezione 2.1: Prerequisiti trigonometrici Su Capitolo 2: Serie di Fourier e spazio dei segnali Sezione 2.3: Teorema di Parseval