Finestratura e stima spettrale

Prev Sezione 3.7: Treno di impulsi Su Capitolo 3: Trasformata di Fourier e convoluzione Capitolo 4: Campionamento quantizzazione ed elaborazione numerica Next

3.8 Appendici

3.8.1 Grafico della trasformata di un rettangolo ritardato

Affrontiamo il problema definito a pag. 1. Conviene iniziare esprimendo X(f) = τsinc(fτ) come

X(f) = τ|sinc(fτ)|e^jφ(f)

in cui, adottando la funzione sgn(x) = ^x⁄_|x| (pag. 42),

φ(f) = π2 {1 − sgn[sinc(fτ)]} ⋅ sgn(f)

alterna valori tra 0 e π in funzione del segno del sinc, in modo che quando sinc è negativo la fase sia π e dunque il fattore e^jπ = − 1 ristabilisce il suo corretto valore. Inoltre, il prodotto per sgn(f) rende la fase un segnale dispari.

L’esercizio chiedeva di calcolare la trasformata di z(t) = x(t − T) = rect_τ(t − T), e dunque possiamo dire che la traslazione temporale del rect determina per Z(f) uno spettro di modulo ancora pari a |Z(f)| = τ|sinc(fτ)|, mentre alla fase φ(f) si aggiunge il contributo lineare in f pari a φ(f) = − 2πfT, ottenendo quindi

Z(f) = τ|sinc(fτ)|e^{j(φ(f) − 2πfT)}

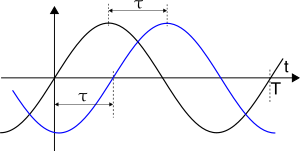
che viene rappresentato in figura, avendo posto τ = 2 e T = .5.

3.8.2 Misura di una differenza di fase

Come suggerito a pagina 1, esaminiamo come valutare una differenza di fase tra due sinusoidi, ad esempio quando vogliamo misurare la risposta di fase di un sistema. A questo scopo, prendiamo il grafico (letto su un oscilloscopio a doppia traccia) dove due sinusoidi con periodo uguale T hanno un ritardo τ. Dobbiamo in effetti valutare la semplice proporzione

τ : T = φ : 2π

in modo da ottenere

φ = 2π τT

ma ora notiamo che la curva blu ha un ritardo, quindi la sua fase rispetto al seno nero è − φ. Ma forse la domanda a monte è: perché un intero periodo T equivale a un angolo uguale a 2π?? Ecco...

in primo luogo si noti [133] [133] Vedi https://www.geogebra.org/m/sgBZefns per una animazione che il rapporto tra la circonferenza C e il diametro d di ogni cerchio è 3.14159… = π, ovvero Cd = π;
si consideri quindi che il diametro d è doppio del raggio, cioè d = 2r, cosicché Cr = 2π;
in conclusione quando un punto, ruotando su una circonferenza di raggio unitario, ha compiuto un giro completo, ha percorso una distanza di 2π.

3.8.3 Quanti sono i possibili modi di calcolare una trasformata?

Sia dato il segnale

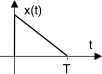
x(t) = ⎧⎨⎩ 1 − tT con 0 ≤ t ≤ T 0 altrimenti

mostrato in figura. Descrivere quanti più modi possibili di calcolarne lo spettro di densità di energia E_x(f).

Si calcola X(f) = F {x(t)} = ∫^∞_−∞x(t)e^−j2πftdt e quindi E_x(f) = |X(f)|²;
Notando che x(t) = y(t) ⋅ z(t) con y(t) = tri_2T(t) e z(t) = rect_T⎛⎝t − T2⎞⎠, possiamo scrivere X(f) = Y(f) * Z(f), e quindi si procede come in 1);
Notiamo che la derivata [134] [134] La derivata di una discontinuità di prima specie è pari ad un impulso di Dirac, di area uguale all’altezza della discontinuità. Infatti l’integrale dell’impulso ∫^t_−∞δ(θ)dθ è proprio un gradino. Questa considerazione consente di risolvere in modo semplice le trasformate di segnali in cui è presente una discontinuità. di x(t) vale g(t) = ddtx(t) = δ(t) − 1T rect_T⎛⎝t − T2⎞⎠; questo ci permette di calcolare G(f) come
G(f) = F {g(t)} = 1 − sinc(fT) ⋅ e^−jπfT
Otteniamo quindi X(f) = G(f)j2πf, e quindi come in 1);
Anticipando un risultato del § 7.2.1, è possibile calcolare R_x(τ) = ∫^∞_−∞x(t)x(t + τ)dt, e quindi E_x(f) = F {R_x(τ)}.

3.8.4 Finestratura e stima spettrale

Applichiamo ora la teoria svolta al § 3.5.2 per speculare sull’interpretazione della trasformata di x(t) svolta a partire da un segmento y(t) ottenuto delimitando x(t) nel tempo mediante moltiplicazione per una funzione finestra di durata limitata w(t). La trasformata di y(t) = x(t)w(t) fornisce infatti il valore Y(f) = X(f) * W(f), e quindi il vero spettro X(f) di x(t) non può essere conosciuto, se non tramite l’effetto della convoluzione con quello W(f) della funzione finestra w(t): in questo caso si parla dunque più propriamente di stima spettrale (vedi § 7.3). Già a pagina 1 si è fatto notare come, se x(t) = Acos2πf₀t e w(t) = rect_T(t), si ottiene che W_rect(f) = T sinc(fT), e pertanto

F {x(t) ⋅ w(t)} = AT2(sinc[(f − f₀)T] + sinc[(f + f₀)T])

tanto più diverso dai due impulsi del coseno (vedi Fig. 3.14), quanto più è piccolo T.

Valutiamo ora gli effetti derivanti dall’uso di una funzione finestra diversa da quella rettangolare. Se ad esempio si sceglie di adottare una finestra triangolare di eguale durata T, a partire dalla (10.57) si ottiene

W_tri(f) = F {w(t) = tri_T(t)} = T2 ⎡⎣sinc⎛⎝fT2⎞⎠⎤⎦²

Come può essere verificato dalla figura a fianco,

la finestra triangolare esibisce un andamento nel tempo più dolce (non ha discontinuità di prima specie) rispetto al rect(t), e ciò si riflette in una maggiore concentrazione della sua trasformata alle frequenze più basse. Infatti W_tri(f) ha un lobo principale di estensione doppia rispetto a W_rect(f) (il primo zero si trova ad f = 2T anziché ad 1T), mentre le code laterali decrescono più rapidamente, andando a zero come 1f²; infine, il valore W_tri(f = 0) risulta dimezzato, così come l’area della w_tri(t).

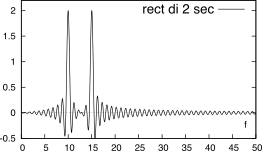
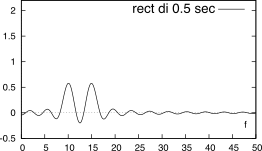
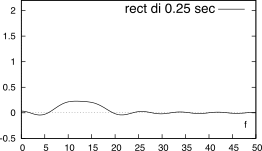
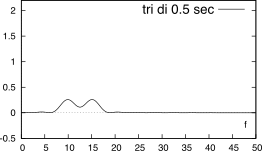
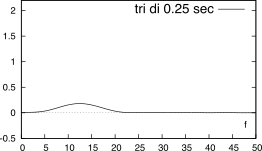
L’andamento del lobo principale e delle code di W(f) si riflette nell’andamento della trasformata del segnale finestrato qualora il segnale originario contenga, ad esempio, più di una frequenza: per la linearità della trasformata, il risultato sarà la replica di W(f) centrata alle frequenze presenti. La Fig. 3.25 confronta il risultato ottenibile per un segnale contenente due cosinusoidi di frequenza f₀ = 10 e f₁ = 15 Hz, quando delimitato (a sinistra) mediante una finestra rettangolare di durata (dall’alto in basso) T = 2, 0.5, e 0.25 secondi [135] [135] Queste durate corrispondono quindi ad utilizzare 20 cicli di cosinusoide, oppure 5, oppure due e mezzo., oppure (a destra) mediante una finestra triangolare della stessa durata. E’ possibile distinguere due effetti.

Figure 3.25 Trasformata di due toni a 10 e 15 Hz, con finestra temporale rect_T(t) e tri_T(t) di durata 2, 0.5 e 0.25 secondi

Risoluzione spettrale

Osserviamo che al diminuire del prodotto (f₁ − f₀) ⋅ T, le due trasformate W(f) interagiscono, fino ad esibire un andamento complessivo in cui non è più possibile distinguere la presenza di due diversi toni. Il fenomeno illustrato avviene tanto prima, quanto più il lobo principale di W(f) è esteso; pertanto, l’uso di una finestra triangolare peggiora la situazione: in effetti, la finestra rettangolare è quella che permette la migliore capacità di distinguere due toni.

Infiltrazione spettrale

Detto leakage in inglese, indica l’influenza che una determinata componente spettrale ha nei confronti delle altre porzioni dello spettro: ad esempio, la prima riga di fig. 3.25 mostra come adottando w(t) = tri_T(t) si ottiene un Y(f) più simile a quello di due toni, piuttosto che con un rect_T(t). Ciò è dovuto alle ampie code di W_rect(f) = T sinc(fT) che appunto infiltrano il contenuto energetico di ciascun tono a frequenze anche distanti, mentre nel caso di w(t) = tri_T(t) ciò avviene in forma assai ridotta, evitando di mostrare artefatti.

Considerazioni di questo tipo possono far preferire una tra le diverse possibili proposte [136] [136] Nel tempo sono state definite un elevato numero di finestre temporali, ognuna migliore sotto certi aspetti, e peggiore sotto altri. Consultando Wikipedia http://en.wikipedia.org/wiki/Window_function, possiamo elencare le finestre di Hamming, Hann, Cosine, Lanczos, Bartlett, Gauss, Blackman, Kaiser, Nuttall, Bessel, Dolph-Chebyshev, Exponential, Tukey.... di funzione finestra, in dipendenza dal particolare obiettivo della stima spettrale (§ 7.3).

3.8.5 Gli esponenziali complessi come base ortogonale

Al § 3.1 sono esposte similitudini tra la serie e la trasformata di Fourier; chiediamoci ora se le funzioni e^j2πft possano anche in questo caso essere considerate come una base ortonormale (pag. 1), e se la (10.31) sia una proiezione di x(t) lungo tali vettori.

Un primo ostacolo è rappresentato dal fatto che ora la cardinalità dello spazio di rappresentazione risulta veramente infinita, e non più infinita numerabile come per la serie. Ma l’ostacolo maggiore sembra essere che le funzioni e^j2πft non sono segnali impulsivi, e neanche di energia: infatti e^j2πfte^−j2πft = 1, e dunque la definizione di prodotto scalare (10.35) e di norma fornisce ∫^∞_−∞e^j2πfte^−j2πftdt = ∞. Ma se proviamo ad effettuare il calcolo del prodotto scalare tra due esponenziali e^j2πft ed e^j2πλt come risultato di un passaggio al limite, otteniamo

lim_{τ → ∞}^{^τ⁄₂}⌠⌡_{− ^τ⁄₂}e^j2πfte^−j2πλtdt = lim_{τ → ∞}^{^τ⁄₂}⌠⌡_{− ^τ⁄₂}e^{j2π(f − λ)t}dt = lim_{τ → ∞} τ ⋅ sinc((f − λ)τ) = δ(f − λ)

in cui si è fatto uso del risultato (10.33) e del fatto che l’ultimo limite tende ad un impulso di Dirac, come mostrato al § 3.4, ottenendo che ⟨e^j2πft, e^j2πλt⟩ = δ(f − λ) = ⎧⎨⎩ 0 se f ≠ λ ∞ se f = λ . Se poi applichiamo agli esponenziali la definizione di prodotto interno per segnali di potenza (10.28), si ottiene che

⟨e^j2πft, e^j2πλt⟩_pot = lim_{τ → ∞} 1τ τ sinc((f − λ)τ) = ⎧⎨⎩ 0 se f ≠ λ 1 se f = λ

permettendo dunque di dichiarare la base {e^j2πft} come ortonormale per lo spazio dei segnali di potenza.

Effettivamente, visto che l’introduzione dell’impulso δ(.) permette di estendere l’operatore di trasformata di Fourier anche al caso dei segnali periodici (pag. 1), che sono di potenza, sembra sensato considerare quest’ultimo come lo spazio corretto in cui individuare le funzioni della base che permette la rappresentazione x(t) = ∫^∞_−∞X(f)e^j2πftdf dei segnali x(t) nei termini della corrispondente trasformata di Fourier X(f) = ∫^∞_−∞x(t)e^−j2πftdt.

3.8.6 Trasformata di un gradino

Definiamo la funzione gradino [137] [137] Nota anche come funzione di Heaviside, vedi
https://it.wikipedia.org/wiki/Funzione_gradino_di_Heaviside come u(t) = ⎧⎨⎩ 1 per t > 0 12 per t = 0 0 per t < 0 che, fornendo ∫^∞_−∞|u(t)|dt = ∞, non dovrebbe avere una trasformata U(f). Proviamo allora a gestire il gradino nelle vesti di una distribuzione, ed in modo simile a quanto fatto al § 91 per la costante, lo rappresentiamo come il limite a cui tende una successione u(t) = lim_α → 0 u_α(t), dei cui elementi valutare la trasformata U_α(f) = F {u_α(t)}, e adottare U(f) = lim_α → 0 U_α(f) come trasformata di u(t). Scegliamo quindi u_α(t) = e^− αt per t > 0 che effettivamente converge a u(t) per α → 0, e troviamo

(10.65)
U_α(f) = ^∞⌠⌡₀ e^− αte^−j2πftdt = e^{− (α + j2πf)t} − (α + j2πf)|||^∞₀ = 1α + j2πf = α − j2πfα² + (2πf)²

Mentre per la parte immaginaria risulta che

U^Im(f) = lim_α → 0ℑ{U_α(f)} = lim_α → 0 − 2πfα² + (2πf)² = − 12πf

e va bene così, il limite della parte reale della (10.65) U^Re(f) = lim_α → 0 αα² + (2πf)² assume invece la forma indeterminata 00 se anche f → 0. Per tentare di capire cosa manca, proviamo ad antitrasformare jU^Im(f), ottenendo

F ⁻¹⎧⎩ − j2πf⎫⎭ = ^∞⌠⌡_−∞e^j2πftj2πf df = ^∞⌠⌡_−∞cos2πftj2πf df + j^∞⌠⌡_−∞sin2πftj2πf df = = ^∞⌠⌡_−∞sin2πft2πf df = t^∞⌠⌡_−∞sinc(2ft) df = t2|t| = 12 sgn(t)

dato che cos2πftj2πf è una funzione dispari e dunque dà integrale nullo [138] [138] Ciò è vero purché si consideri il metodo di calcolo dell’integrale noto come valore principale di Cauchy , in quanto cos2πftj2πf tende a 10 per f → 0, con valori opposti per 0⁺ e 0⁻, vedi
https://it.wikipedia.org/wiki/Valore_principale_di_Cauchy. , mentre la penultima uguaglianza sfrutta il risultato (10.39). Ci siamo quasi! Infatti, il gradino può essere riscritto come u(t) = 12 + 12 sgn(t) (vedi la figura a lato), e in questo modo ci accorgiamo che mentre jU^Im(f) = − j2πf è la trasformata di 12 sgn(t), U^Re(f) deve necessariamente convergere alla trasformata di 12, ovvero ad un impulso di area 12, permettendo finalmente di scrivere

U(f) = F {u(t)} = 12 ⎛⎝δ(f) − jπf⎞⎠

Sembrano conti troppo contorti? In realtà l’abbiamo fatta semplice... [139] [139] Vedi ad es. http://bueler.github.io/M611F05/M611heaviside.pdf.

3.8.7 Proprietà della trasformata di Fourier

Uno schema riassuntivo delle relazioni illustrate nel capitolo

Proprietà	z(t)	Z(f) = F {z(t)}
Linearità	ax(t) + by(t)	aX(f) + bY(f)
Coniugato	x^*(t)	X^*(−f)
Cambiamento di scala	x(at)	1a X⎛⎝fa⎞⎠
Ritardo	x(t − T)	X(f)e^−j2πfT
Traslazione in frequenza	x(t)e^j2πf₀t	X(f − f₀)
Modulazione di ampiezza	x(t)cos2πf₀t	12X(f − f₀) + 12X(f + f₀)
Prodotto in frequenza	∫^∞_−∞x(τ) y(t − τ) dτ	X(f)Y(f)
Prodotto nel tempo	x(t)y(t)	∫^∞_−∞X(σ) Y(f − σ) dσ
Dualità	X(t)	x(−f)
Simmetria coniugata	x(t) reale	X(f) = X^*(−f)
Derivazione	ddt x(t)	j2πf ⋅ X(f)
Integrazione	∫^t_−∞x(θ)dθ	X(f)j2πf + 12 δ(f)X(0)

3.8.8 Trasformate di segnali

Un sommario dei risultati per alcune trasformate

x(t)	X(f)	P ⁄ E	P(f) ⁄ E(f)	Pot/En
cos(2πf₀t + φ)	12 e^jφδ(f − f₀) +	12	14δ(f − f₀) +	P
	12 e^−jφδ(f + f₀)		14δ(f − f₀)
A	A ⋅ δ(f)	A²	A² ⋅ δ(f)	P
A ⋅ rect_τ(t)	A ⋅ τ sinc(fτ)	A² ⋅ τ	A² ⋅ τ² sinc²(fτ)	E
A ⋅ tri_2τ(t)	A ⋅ τ sinc²(fτ) (¹)	A² ⋅ 23 ⋅ τ	A² ⋅ τ² sinc⁴(fτ)	E
e^− βt, t ≥ 0	1β + j2πf (²)		1β² + 4(πf)²	E
e^− β\|t\|	2ββ² + 4(πf)² (³)		4β²β⁴ + 8(πβf)² + 16(πf)⁴	E
e^{− t²2σ²}	σ√2πe^{− (σ2πf)²2} (⁴)		2πσ² e^{− (σ2πf)²}	E
⎧⎨⎩ 1 con t > 0 0 con t < 0	12⎛⎝δ(f) − jπf⎞⎠ (⁵)
∑^∞_{m = −∞}δ(t − mT)	1T ∑^∞_{n = −∞}δ⎛⎝f − nT⎞⎠ (⁶)

Per il risultato di F { tri_2τ(t)}, vedi esercizio a pag. 1;
per il risultato di F {e^− βt}, vedi nota 205 a pag. 5.1;
per il risultato di F {e^− β|t|}, vedi nota 380 a pag. 7.4;
per il risultato di F {e^{− t²2σ²}}, vedi nota 279 a pag. 6.2;
per la trasformata della funzione gradino, vedi § 3.8.6;
per la trasformata del, treno di impulsi, vedi § 3.7.

Prev Sezione 3.7: Treno di impulsi Su Capitolo 3: Trasformata di Fourier e convoluzione Capitolo 4: Campionamento quantizzazione ed elaborazione numerica Next