4.2 Aspetti realizzativi del campionamento
Mentre lo schema discusso al §
4.1 illustra gli aspetti teorico-matematici del teorema del campionamento
e ne fornisce uno schema operativo di riferimento, nelle implementazioni reali si attuano una serie di stratagemmi volti ad ovviare agli aspetti che in pratica non è possibile realizzare.
Un primo fattore di criticità sono i due filtri
analogici previsti, quello
anti-aliasing e l’altro
di restituzione. Anticipando parte di ciò che sarà discusso al cap.
5, qualsiasi specifica particolarmente stringente si traduce per essi in un aumento del numero di componenti necessari, e quindi del suo costo, oltre che del suo volume. In particolare è pressoché impossibile realizzare una risposta in frequenza
H(f) esattamente rettangolare, mentre ciò che si può fare è un filtro che presenti una
regione di transizione (pag.
1) tra banda passante e banda soppressa di ampiezza non nulla, a cui corrisponde una complessità del filtro tanto minore quanto più la regione è estesa.
4.2.1 Sovracampionamento e decimazione numerica
Anziché tentare di realizzare un filtro anti-aliasing che lasci passare
intatte le frequenze inferiori alla metà della
fc desiderata e blocchi quelle strettamente superiori, se ne adotta uno con una regione di transizione
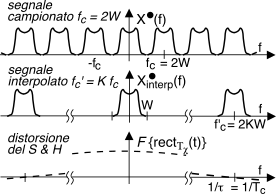
più graduale (seconda riga della fig. a lato),
dunque più facilmente realizzabile, e si adotta una freq. di campionamento pari al doppio della massima frequenza passante (
3W nell’esempio, e dunque
fc’ = 6W), producendo un primo segnale campionato
X•aa(f) privo di aliasing.
I campioni così ottenuti sono quindi elaborati mediante un filtro
numerico, che come vedremo al §
5.2.1 presenta una
Hnumaa(f) periodica in frequenza, può realizzare una regione di transizione assai
più ripida, e sopratutto non altera lo spettro di fase se non per un contributo
lineare (pag.
1). Il segnale campionato
X• filtaa(f) che ne risulta ha ora l’occupazione di banda desiderata di
W (
5a riga di fig.), e la sua frequenza di campionamento può essere
ridotta a quella prevista
fc = 2W operando esclusivamente nel dominio numerico grazie ad uno speciale elemento
decimatore (§
5.4.1), che nel nostro esempio provvede a rimuovere due campioni su tre.
La figura a lato riassume la sequenza delle operazioni descritte.
4.2.2 Generalizzazione del filtro di restituzione
Anche per questo secondo filtro
analogico la teoria prevede l’adozione di un passa basso ideale, ed anche per questo caso valgono le obiezioni già discusse, e dunque la soluzione
semplice a questo problema è quella di adottare una
fc = 2W’ > 2W di lavoro maggiore della minima, ovvero
sovracampionare il segnale, in modo che le repliche spettrali siano più distanziate tra loro, e quindi anche un filtro
non ideale con una regione di transizione non nulla possa ancora isolare l’unica replica di
X•(f) in banda base, come si osserva in figura
4.8.
La conseguenza diretta di questo modo di operare è che non essendo più
H(f) rettangolare, la risposta impulsiva di questo nuovo filtro di restituzione non è più un
sinc(fct)! Ciò significa che in questo caso la formula di interpolazione
non ha più l’espressione
cardinale fornita dalla
(10.66), nella quale evidentemente il
sinc(fct) può essere sostituito da una qualunque
h(t) purchè la relativa trasformata
H(f) si annulli
prima di incontrare una replica spettrale del segnale originario.
4.2.3 Interpolazione numerica
Anziché procedere come appena descritto, si è fatta strada una soluzione ancora differente, che evita di sovracampionare il segnale, dato che questo significherebbe appesantire tutte le operazioni da svolgere nel dominio numerico. La frequenza di campionamento
fc viene invece mantenuta al suo valore minimo consentito dalla selettività del filtro numerico
Hnumaa(f) discusso al (§
4.2.1), ma prima di effettuare la restituzione la freq. di campionamento
fc viene
innalzata per un fattore intero
K, ovvero
f’c = K ⋅ fc, ad opera di un apposito
filtro numerico interpolatore (§
5.4.2) che ogni due campioni ne inserisce nel mezzo altri
K − 1 con valori
intermedi. In tal modo il distanziamento mostrato in fig.
4.8 risulta essere ben maggiore, e le specifiche (pag.
1) per il filtro di restituzione divengono ancora meno stringenti.
4.2.4 Approssimazione degli impulsi
Un ultimo importante aspetto in cui la pratica differisce dalla teoria è che nella fase di restituzione
non è possibile generare il segnale
x•(t) a causa dell’impossibilità di realizzare gli impulsi
δ(t); al suo posto viene prodotto un segnale
x○(t) (leggi
x cerchietto anziché
pallino) mediante l’uso di un circuito
Sample and Hold (
s&
h, ovvero
campiona e mantieni) il cui schema di principio è mostrato in fig.
4.10-a).
Quando
s1 si chiude il valore di tensione di ingresso viene trasferito ai capi del condensatore, dopodiché
s1 si apre e lo stesso valore viene mantenuto costante per un tempo
τ ≤ Tc e reso disponibile in uscita; trascorso il tempo
τ si chiude
s2, il condensatore si scarica, e l’uscita si annulla.
Alle operazioni appena descritte corrisponde lo schema simbolico illustrato in fig.
4.10-b), per il quale il segnale di uscita è descritto nella forma
x○(t) = ∑nx(nTc) ⋅ rectτ(t − nTc) in cui al posto degli impulsi
matematici viene adottato un treno di impulsi
rettangolari modulati in ampiezza (vedi fig.
4.10-c)). Il filtro passa basso di restituzione
H(f) viene ora alimentato da
x○(t) anziché da
x•(t), e per determinare quale sia la sua nuova uscita, riscriviamo
x○(t) nella forma
il cui spettro risulta pari a
Osserviamo quindi che usare rettangoli di base
τ < Tc al posto degli impulsi equivale a moltiplicare
X•(f) per un inviluppo
τ sinc(fτ) che, seppure con
τ ≪ Tc non causa grossi inconvenienti (gli zeri posti ad
1τ si allontanano dall’origine, e
sinc(fτ) nei pressi di
f = 0 è praticamente costante), per
τ prossimo a
Tc produce una alterazione dell’ampiezza della replica in banda base, ovvero un fenomeno di
distorsione lineare di ampiezza (§
8.2).
Una strada per compensare la distorsione lineare dovuta ai
rect del
s&
h si basa sulla conoscenza di
τ per progettare un filtro di restituzione con una
H(f) che presenta un andamento
reciproco di quello del
sinc(fτ), in modo che
H(f) ⋅ τ sinc(fτ) = costante. Tale accorgimento prende il nome di
sinc correction.
Un’alternativa per ridurre l’entità delle distorsione lineare introdotta dal
s&
h anche qualora si scelga la durata
τ dei
rect pari al periodo di campionamento
Tc passa per
l’adozione dell’interpolazione numerica descritta al §
4.2.3 ed approfondita al §
5.4.2, attuata con un fattore di interpolazione
K sufficientemente elevato da rendere tale distorsione praticamente trascurabile, come illustrato in figura
4.2.5 Conversione A/D e D/A
Dopo aver discusso gli aspetti teorici e realizzativi della conversione da segnale analogico
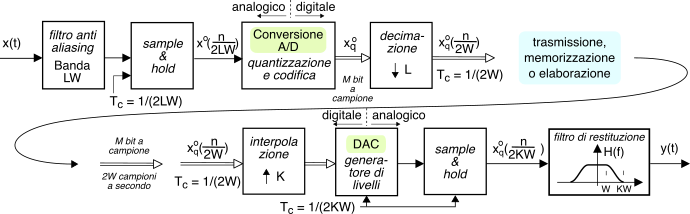
s(t) a sequenza di campioni s•(n) (vedi fig. 1.3 a pag. 1), per completare il processo di digitalizzazione non resta che occuparci del passaggio da s•(n) a segnale quantizzato sq, e da questo a sequenza numerica sn. Infatti, perché il segnale possa essere memorizzato, trasmesso od elaborato in forma numerica, occorre rappresentare i valori dei campioni x(nTc), che sono grandezze a precisione infinita, mediante un numero finito di M bit per campione. La fig. 4.14
inquadra questo ultimo passaggio noto come conversione analogico-digitale (a/d) nel contesto di quanto discusso finora, rappresentando anche l’operazione inversa (dac) che ricostruisce il valore analogico
(sia pur quantizzato) a partire dalla sua codifica binaria. A lato, i simboli usati per rappresentare tutto l’insieme di operazioni in maniera concisa. Senza alcuna pretesa di completezza, illustriamo ora una possibile implementazione dei due dispositivi citati.
Quantizzatore A/D a rampa lineare
Per fissare le idee, descriviamo il funzionamento di uno schema
semplice, con l’ausilio della fig.
4.16. Il valore
x○(nTc) viene confrontato con il segnale
s(t) prodotto dal generatore di rampa, e finché il secondo non supera il valore del primo, il comparatore emette un livello logico vero (il
gate) e quindi il segnale di clock in ingresso all’
and si ripresenta in uscita, facendo avanzare il contatore binario ad
M bit. Quando
s(t) supera
x○(nTc) il
gate si annulla e l’
and viene interdetto, in modo che il conteggio si arresti. Prima di iniziare un nuovo periodo della rampa il valore presente nel contatore (pari a
dieci nell’esempio in figura) viene letto ed adottato come
codifica binaria c(xq) del valore
x○(nTc) in ingresso, ed il processo può ripartire per il campione successivo.
Convertitore D/A
a resistenze pesate
Il generatore di livelli
dac presente in fig.
4.14 consiste in un circuito elettronico in grado di produrre una tensione
Vu proporzionale al valore
Vb codificato da una
parola binaria ad
M bit
Vb = bM − 12M − 1 + ⋯ + b323 + b222 + b12 + b0
posta in ingresso al
dac. Una soluzione
semplice fa uso di un amplificatore operazionale
sommatore come in figura, con ciascuna delle resistenze di ingresso
Ri di valore
2iR (
i da
1 a
M) collegata o meno alla tensione di riferimento
Vr a seconda se il bit
bM − i sia uno o zero. In uscita sarà presente una tensione
Vu = − Vr∑Mi = 1bM − i2 − i
in cui cioè il bit più significativo bM − 1 pesa per 1⁄2, quello successivo per 1⁄4, e così via, dando luogo alla funzione ad L = 2M livelli mostrata in figura.