Capitolo 5: Filtri analogici e numerici Su Capitolo 5: Filtri analogici e numerici Sezione 5.2: Filtri digitali 

5.1 Filtri analogici

Affrontiamo questa classe di filtri senza addentrarci in molti dettagli (svolti in altri corsi), limitandoci a descrivere la metodica di studio. Come anticipato, i filtri analogici operano esclusivamente su segnali tempo-continui [192]   [192] Compreso quindi un segnale analogico che trasporta informazione numerica, § 15.1.2., e sono realizzati mediante una varietà di tecniche. Il tipo più comune è quello basato su circuiti rlc a costanti concentrate, detto filtro passivo in quanto non richiede alimentazione, essendo costituito da condensatori, induttori e resistori. La difficoltà di ottenere elementi di elevata induttanza ma di piccole dimensioni necessari alle frequenze più basse ha portato a realizzarne la funzione per mezzo di amplificatori operazionali [193]   [193] Vedi ad es. https://it.wikipedia.org/wiki/Giratore dando luogo (fino a circa 1 MHz) ai filtri attivi, mentre a frequenze più elevate oltre agli rlc si possono realizzare filtri a cristallo, elettromeccanici, a guida d’onda, a microstrisce [194]   [194] Vedi ad es. https://en.wikipedia.org/wiki/Filter_(signal_processing)#Technologies.
In tutti i casi è possibile svolgere l’analisi del circuito e pervenire [195]   [195] Ad esempio, applicando la trasformata di Laplace alle equazioni differenziali che descrivono la relazione ingresso-uscita di un circuito rlc. all’espressione di una funzione di trasferimento razionale del tipo
(10.90) H(s) = N(s)D(s) = M⎲⎳i = 0aisiN⎲⎳j = 0bjsj
(in cui M < N), definita su di un piano complesso s = σ + j2πf, e ponendo s = j2πf si ottiene la risposta in frequenza [196]   [196] Difatti se s = jπ2f la definizione di trasformata di Laplace H(s) = ∫∞−∞h(t)e − stdt diviene identica a quella di Fourier, ed equivale a calcolare la H(s) lungo l’asse immaginario. Questa equivalenza è valida solo se il filtro è stabile, che nel dominio di Laplace significa richiedere che tutti i poli di H(s) siano a sinistra di tale asse. H(f) = H(s = j2πf). Il grado N del denominatore di (10.90) (uguale al numero delle sue radici o poli) definisce l’ordine del filtro, ed è legato sia alla sua complessità realizzativa, sia alla rapidità di variazione della H(f).
Tipo di polinomio e di filtro
Lo spazio di progetto del filtro viene delimitato vincolando i polinomi N(s) e D(s) ad appartenere ad una delle famiglie dette di Bessel, di Butterworth, di Chebyschev o di Cauer (o filtri ellittici) [197]   [197] Per approfondimenti, si può consultare http://ens.di.unimi.it/dispensa/cap3.pdf e
https://en.wikipedia.org/wiki/Network_synthesis_filters.
, che essenzialmente differiscono tra loro per la posizione delle radici del polinomio nel piano s; la figura 5.2 mostra il modulo della risposta in frequenza H(f) di un filtro passa-basso ottenibile nei diversi casi per uno stesso ordine N = 5.
figure f7.22.5.png
Figure 5.2 Risposta in frequenza di un filtro passa basso per diverse famiglie polinomiali
figure Bandform_template.png
Per ogni famiglia esistono tabelle di coefficienti precalcolati per diversi valori di N e che danno luogo ad un filtro passo-basso prototipo ovvero con frequenza di taglio (vedi sotto) unitaria, dai quali si ottengono (mediante operazioni di cambio di variabile) i nuovi coefficienti per frequenze di taglio qualsiasi e per filtri con altro tipo di banda passante, ossia passa-alto, passa-banda e arresta-banda (o notch) [198]   [198] Vedi ad es. https://en.wikipedia.org/wiki/Prototype_filter; gli ultimi due casi sono inoltre realizzabili anche rispettivamente come cascata o parallelo di un passa-alto più un passa-basso, con frequenze di taglio opportune.
Specifiche di progetto, ordine del filtro e scelta del polinomio
L’ordine del filtro viene individuato come quello per il quale il modulo della risposta in frequenza |H(f)| (o meglio, il suo quadrato) associata al polinomio prescelto rientra all’interno della maschera definita da uno
figure f7.22.4.png
schema di tolleranza del tipo [199]   [199] La descrizione della maschera in figura avviene nei termini della specifica di
  • puna banda passante f < fp che individua la regione di frequenze da lasciar passare;
  • il valore percentuale δ1 entro cui H(f) può oscillare nella banda passante;
  • una banda soppressa f > fs in cui vorremmo che le corrispondenti componenti frequenziali in ingresso fossero attenuate di almeno il δ2% rispetto a quelle della banda passante;
  • una banda di transizione fs − fp in cui la risposta in frequenza varia;
  • se sia richiesta o meno al filtro la proprietà di linearità di fase (vedi § 13.1.3).
mostrato nella figura a lato. La specifica è tanto più stringente quanto più |H(f)| varia rapidamente, cosa possibile solo aumentando l’ordine N. Ma non tutti i polinomi si comportano allo stesso modo, anzi, come evidente guardando la fig. 5.2 da sin. a destra, a parità di ordine alcuni permettono transizioni assai più rapide rispetto ad altri. D’altra parte per molte applicazioni è anche necessario garantire una buona linearità di fase (pag. 1, § 8.2.2) da parte del filtro, ma in linea generale questa seconda esigenza è incompatibile con una elevata selettività (vedi sotto) del filtro. In particolare i filtri di Bessel  [200]   [200] Vedi ad es. https://en.wikipedia.org/wiki/Bessel_filter sono gli unici ad esibire una fase lineare, ma decadono lentamente con la frequenza; per gli altri tipi di fig. 5.2 la linearità di fase peggiora all’aumentare della selettività, specie in prossimità della frequenza di taglio. Quindi in definitiva la scelta del polinomio viene effettuata in base alla specifica sulla fase, e l’ordine N del filtro determinato in base alla maschera di attenuazione.
Frequenza di taglio, selettività e fattore di qualità
Sono parametri che descrivono un filtro in modo grossolano ma indicativo. La frequenza di taglio fT è quella per la quale
(10.91) |H(ft)|2 = 12 |H(f)|2Max
e dunque individua una sorta di frontiera tra la banda passante e quella soppressa. La selettività di un passa basso è misurata dal rapporto
k = fpfs ≤ 1
(l’inverso per un passa-alto) ed è tanto più grande quanto meno estesa è la regione di transizione. Nel caso di un passa-banda centrato in f0 il filtro può inoltre essere caratterizzato nei termini del suo fattore di qualità
Q = f0B
in cui B = fT2 − fT1 è la banda compresa tra le due frequenze di taglio inferiore e superiore; Q rappresenta pertanto quanto il filtro è stretto attorno alla sua risonanza, ed il suo inverso B⁄f0 è chiamato banda frazionaria.
Realizzazione del filtro
Mentre i filtri di Bessel, Butterworth e Chebyshev-I sono filtri a soli poli, quelli di Chebyshev-II ed Ellittici possiedono anche zeri. Ma in entrambi i casi una volta noti i coefficienti, la (10.90) si riscrive in forma fattorizzata [201]   [201] Un polinomio P(s) = ∑Nj = 0bjsj si azzera per gli N valori s = βj, noti come gli zeri di P(s). Lo stesso polinomio può quindi essere scritto come P(s) = ∏Nj = 1(s − βj), oppure raggruppando gli zeri a coppie (eventualmente coniugate) si ottiene uno sviluppo in termini di secondo grado P(s) = ∏N⁄2j = 1(s2 + cjs + dj) a cui, se N è dispari, va aggiunto un fattore di primo grado. H(s) = ∏N⁄2j = 1Hj(s) con ogni termine Hj(s) che presenta una coppia di poli coniugati e che corrisponde ad un circuito risonante del secondo ordine o cella circuitale [202]   [202] Tradizionalmente di tipo rlc, oppure realizzata mediante amplificatori differenziali., producendo il massimo per |Hi(j2πf)|2 alla frequenza di risonanza fi0. Ponendo le diverse celle in cascata si ottiene così la H(f) che soddisfa i requisiti stabiliti dallo schema di tolleranza.
Nonostante quanto discusso appaia direttamente applicabile al solo caso di segnale analogico, al § 5.3 mostreremo come i risultati ottenuti siano applicabili anche al caso di segnali numerici, dato che esistono tecniche (basate su cambi di variabile che mappano il semipiano sinistro della variabile s all’interno del cerchio unitario del piano z) che permettono di passare da una H(s) ad una H(z), e di lì ad una realizzazione del filtro in forma numerica.

5.1.1 Filtro analogico ad un polo

A titolo di esempio esemplificativo di quanto fin qui illustrato, occupiamoci del più semplice tipo di filtro analogico, costituito dal partitore rc rappresentato alla figura seguente, e che realizza una funzione di passa-basso [203]   [203] Mnemonicamente possiamo ricordare il passa-basso come quello “con il condensatore in basso”; d’altra parte un filtro rc passa-alto presenta la posizione di r e c scambiate, ovvero con c in alto..
Considerando la tensione vi(t) come il segnale di ingresso al filtro, mostriamo
figure f7.23.png
che la corrispondente uscita vu(t) può essere espressa come convoluzione tra vi(t) ed una risposta impulsiva
(10.92) h(t) = 1RCe − tRC con t ≥ 0
L’analisi del circuito porta infatti [204]   [204] Sappiamo che le tensioni ai capi di R e C valgono vR(t)) = R ⋅ i(t) e vC(t) = vu(t) = 1C ∫t−∞i(τ)dτ che, trasformate con Fourier forniscono VR(f) = R ⋅ I(f) e Vu(f) = 1C 1j2πf I(f). Per la legge di Kirkoff alle maglie si ha Vi(f) = VR(f) + Vu(f) = R ⋅ I(f) + 1j2πfC I(f); la risposta in frequenza sarà pertanto H(f) = Vu(f)Vi(f) = 1j2πfC I (f)R ⋅ I(f) + 1j2πfC I(f) = 11 + j2πfRC. ad una espressione per la risposta in frequenza pari a
(10.93) H(f) = 11 + j2πfRC
di cui la (10.92) è l’antitrasformata [205]   [205] Infatti F ⎧⎩1τe − t⁄τ⎫⎭ = ∫∞01τe − t⁄τe −j2πftdt = 1τ ∫∞0e − t⁄τ − j2πftdt = 1τ e − t⁄τ − j2πft − 1⁄τ − j2πf|t = ∞t = 0 = 1τ 11⁄τ + j2πf = 11 + j2πfτ
. Estendendo questo risultato al dominio di Laplace si ottiene
H(s) = 11 + sRC
Pertanto, H(s) presenta un polo in s = − 1RC, e dunque risulta H(s)|s = − 1RC = ∞.
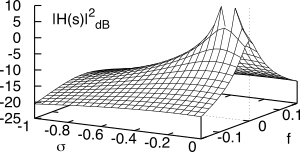
figure f7.24.png
A lato è raffigurato l’andamento di 10 log10|H(s)|2 calcolato per un valore RC = 8. Come evidente, |H(s)|2 può essere pensata come una sorta di cono vulcanico attorno al polo sito in 1⁄RC = 0.125 e la cui sezione, ottenuta dall’intersezione con un piano verticale passante per l’asse j2πf, individua la risposta in frequenza H(f) = H(s = j2πf). Come si vede dalla figura, H(f) risulta di tipo passa basso, con fianchi tanto più ripidi quanto più il polo è vicino all’origine.
Frequenza di taglio
figure f7.25.png
Nel caso del filtro RC risulta che |HMax| = H(0) = 1, ed esprimendo il modulo della (10.93) nella forma [206]   [206] Ricordiamo che il modulo è il rapporto dei moduli, e quello del denominatore è √ℜ2 + ℑ2 in cui dalla (10.93) ℜ = 1 e ℑ = 2πfRC.
|H(f)| = 1√1 + (2πfRC)2 = 1√1 + ⎛⎝ffT⎞⎠2
si pone in evidenza che fT = 12πRC rappresenta proprio la frequenza di taglio: infatti, |H(fT)| = 1√1 + 1 = 1√2. Cogliamo l’occasione per notare che risultando (eq.- (10.91)) |H(fT)|2 = 12 H2Max si ottiene [207]   [207] Vedi § 8.1 che |H(fT)|2|dB = H2Max(dB) − 3; per questo la frequenza di taglio è indicata anche come frequenza a 3 dB.
 Capitolo 5: Filtri analogici e numerici Su Capitolo 5: Filtri analogici e numerici Sezione 5.2: Filtri digitali