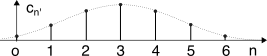5.2 Filtri digitali
Con questo termine indichiamo una classe di filtri definita mediante uno
schema computazionale anziché circuitale, espresso unicamente nei termini di unità elementari di elaborazione
prodotto, somma e ritardo (§
7.5) che (in combinazione tra loro) producono effetti filtranti sul segnale in transito. Essi possono rappresentare un modello di cause naturali, oppure si può progettare una specifica architettura in modo da combinare questi elementi per ottenere l’effetto desiderato. Per questa classe di filtri l’integrale di convoluzione si riduce ad una sommatoria, e sebbene l’analisi che segue si basi su segnali
tempo-continui, i filtri digitali sono di particolare rilievo perché permettono di svolgere le operazioni di filtraggio operando direttamente sui
campioni dei segnali (vedi §
4.6.1), e dunque possono essere realizzati via software o hardware.
5.2.1 Filtro trasversale
Prende questo nome dal modo in cui è rappresentato lo schema di calcolo, vedi la fig.
5.7,
in cui l’uscita
y(t) (in basso a destra) è ottenuta sommando valori di ingresso
x(t) (in alto a sinistra) presi (grazie alla cascata di ritardi) ad istanti
t = nT con
n = 0, 1, ⋯N, ognuno moltiplicato per un diverso coefficiente
cn, ovvero
Se poniamo in ingresso
x(t) = δ(t), l’uscita
y(t) riprodurrà la
risposta impulsiva del filtro, pari a
costituita da
N + 1 copie dell’impulso posizionate in
t = nT e con area pari ai rispettivi coefficienti
cn o
rubinetti del filtro. All’intero
N viene conferito il senso di
ordine del filtro, ed essendo finito, permette di classificare questa architettura come un filtro
fir (
finite impulse response). Applicando le relazioni note della trasformata, è facile valutare la risposta in frequenza corrispondente alla
h(t) (10.95), ovvero
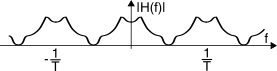
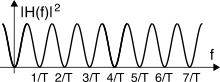
Come esemplificato dalla figura a lato,
H(f) risulta periodica (in frequenza) con periodo
F = 1T: infatti tutti gli esponenziali
e −j2πfnT della sommatoria
(10.96) presentano la stessa periodicità.
Al §
4.4 abbiamo già incontrato segnali con spettri periodici: la trasformata discreta di Fourier
dtft (eq.
(10.73))
H•(f) calcolata a partire da un segnale campionato
h•(t) espresso nella forma
(10.95) ha esattamente l’aspetto della
(10.96), che quindi riscriviamo come
H(f) = H•(f) = ⎲⎳∞n = −∞G⎛⎝f − n T ⎞⎠
ovvero come risposta in frequenza
periodizzata del filtro
G(f) limitato nella banda
⎛⎝− 1 2T , 1 2T ⎞⎠ che intendiamo ottenere. A questo punto i coefficienti
cn che definiscono
h(t) altro non sono che quelli (
nel tempo) dello sviluppo in serie di Fourier di
H•(f) (periodica
in frequenza con periodo
1⁄T), ovvero (eq.
(10.74))
Ora però sorgono due problemi. Il primo è che la
(10.97) è valida con
n = −∞, ⋯, ∞, mentre noi vorremmo solamente
N + 1 coefficienti
cn. A questo c’è rimedio a patto di accettare una approssimazione,
finestrando la sequenza dei
cn e tenendo così solo quelli per
n = − N⁄2, ⋯, N⁄2: ovviamente più è piccolo
N, e peggiore sarà l’approssimazione
Ĥ(f) di
H(f). Il secondo problema è che nella
(10.96) ed in fig.
5.7 i coefficienti hanno indici
≥ 0, e non negativi, come deve essere per ottenere un sistema
fisicamente realizzabile (pag.
1). A ciò si risponde eseguendo
uno scorrimento a destra dei
cn di
N⁄2 posizioni, assegnando
cn’ = cn + N⁄2 in modo da avere
n’ ∈ [0, ⋯, N]: questo corrisponde ad introdurre un ritardo nell’uscita pari a
N2 T , ottenendo così un segnale
ỹ(t) = y⎛⎝t − N 2 T⎞⎠.
Un vantaggio della approssimazione ora descritta è la possibilità di ottenere facilmente un filtro detto a
fase lineare, ovvero per cui
arg{H(f)} = e −j2πfτ e che dunque non presenta distorsione di fase (§
13.1.3). Infatti scegliendo
H(f) reale pari si ottengono valori
cn reali pari (vedi §
2.2.1.1), e lo scorrimento per produrre i
cn’ è l’unico contributo alla fase della
H̃(f) = Ĥ(f) e −j2πf N 2 T risultante. In definitiva, operare in questo modo determina valori dei
cn simmetrici rispetto ad
N⁄2.
5.2.2 Realizzazione numerica del filtro trasversale
Lo schema di fig.
5.7 è completamente
analogico, nel senso che sia
x(t) che
y(t) sono definiti per ogni
t. D’altra parte, la presenza degli
N ritardi
T tutti uguali permette di derivarne uno schema
di calcolo operante su segnali campionati con frequenza
fc = 1 Tc . A questo scopo è sufficiente scegliere
T = Tc = 1 fc e calcolare
y(t) ai soli istanti
t = nT, così come
caricare la memoria del filtro con i soli campioni
x(nT): infatti, al §
4.6.1 si mostra che se due segnali
x(t) ed
h(t) sono limitati in una banda
W, e se
Tc < 1⁄2W la
convoluzione discreta
tra i relativi campioni
xn ed
hn produce una terza sequenza
yk da cui, applicando il teorema del campionamento, si ottiene lo stesso risultato della convoluzione analogica
y(t) = x(t) * h(t).
Se ora limitiamo l’indice
n tra zero ed
N (la durata di
hn), la
(10.98) equivale alla
(10.94) calcolata per
t = kTc ovvero
y(kTc) = ∑Nn = 0cnx((k − n)Tc), dopo aver posto
cn = Tc hn
Sebbene la condizione di limitatezza
temporale dovrebbe escludere quella di limitazione
in banda, i valori
hn possono essere associati in prima approssimazione ai
campioni (presi per
t = nTc) della risposta impulsiva
h(t) = F −1{H(f)} corrispondente alla
H(f) desiderata. Ovviamente, i campioni (di
x(t),
y(t) e
h(t)) devono essere presi ad intervalli
T = Tc ≤ 1⁄2W, in cui ora
W è la
massima frequenza massima tra
x(t) ed
h(t).
Esempio Si desideri realizzare un filtro trasversale che approssimi una H(f) = tri2B(f), considerando che al suo ingresso è posto un processo bianco x(t) con densità di potenza Px(f) = N0 2 rect4B(f). Per realizzare il filtro numerico operante su dati campionati occorre adottare una frequenza di campionamento
fc ≥ 2W = 4B, e dunque un ritardo tra gli stadi del
fir pari a Tc ≤ 1⁄4B, in modo che la corrispondente H•(f) presenti la periodicità fc = 4B mostrata in figura.
In base alle considerazioni precedenti, dopo aver ottenuto h(t) = F −1{H(f)} = Bsinc2(tB), ne calcoliamo i campioni per t = nTc = n⁄4B ovvero hn = Bsinc2⎛⎝n 4 ⎞⎠, da cui otteniamo cn = Tchn = 1 4 sinc2⎛⎝n 4 ⎞⎠.
A questo punto non resta che troncare la serie a pochi termini centrati in zero (ad es. con n = −3, −2, −1, 0, 1, 2, 3 tutti i campioni di h(t) sono prelevati dal lobo principale del sinc2) accettando l’approssimazione conseguente, e traslarli a destra in modo da ottenere un filtro causale con sette rubinetti, nell’esempio cn’ con n’ = 0, 1, ⋯, 6, con coefficienti simmetrici rispetto ad n = 3, e dunque il filtro è a fase lineare. A lato sono mostrati i coefficienti ottenuti, assieme alla Ĥ(f) risultante dalla loro finestratura.
Quando i coefficienti
cn sono tutti uguali tra loro e con valore pari ad
1N + 1 le operazioni condotte dal filtro sono dette di
media mobile (da
moving average o
ma) dato che di fatto si calcola una media aritmetica tra gli ultimi valori di ingresso, ovvero
yk = 1 N + 1 ∑Nn = 0xk − n. E’ il metodo comunemente usato per
smussare serie temporali discrete, come per es. temperature (giornaliere od orarie) o quotazioni dei titoli di borsa. Corrisponde ad un filtro tempo-continuo la cui
h(t) è una
rect(N + 1)Tc(t), ha un effetto passa-basso, e la relativa
H(f) è ottenuta a pag.
1.
Filtro passa-alto e passa-banda
Il filtro trasversale può essere configurato come
un
passa-alto considerando un segnale in ingresso limitato in banda
W = fc 2 = 1 2T ed impostando la
H•(f) in modo da tener conto della sua periodicità in frequenza pari ad
fc, come mostrato in figura. Può altresì divenire un filtro
passa-banda sempre per il medesimo tipo di segnale, con il vincolo di lasciar passare le frequenze centrate attorno ad
fc 4 .
Occupiamoci ora di un paio di architetture particolarmente semplici: la prima è ancora un fir ma con N = 1, mentre la seconda introduce la classe di filtri di tipo infinite impulse response o iir. Anche se per entrambi è chiaramente possibile realizzare una implementazione numerica qualora il ritardo T = 1⁄fc sia tale da permettere il campionamento del segnale in ingresso, qui analizziamo solo gli aspetti tempo-continui.
5.2.3 Filtro trasversale del primo ordine
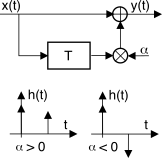
Con
N = 1 il filtro di fig.
5.7 può essere ridisegnato come mostrato a lato, avendo posto
c0 = 1 e
c1 = α. Ad esso corrisponde una risposta impulsiva
il cui andamento è mostrato a fianco per i casi
α≷0, ed a cui corrisponde una risposta in frequenza pari a
H(f) = 1 + αe −j2πfT. Da questa espressione è facile ottenere quella del guadagno di potenza
|H(f)|2, che risulta
|H(f)|2 = (ℜ{H(f)})2 + (ℑ{H(f)})2 = (1 + αcos2πfT)2 + (αsin2πfT)2 = = 1 + 2αcos2πfT + α2(cos22πfT + sin22πfT) = = 1 + α2 + 2αcos2πfT
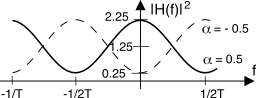
La figura che segue mostra l’andamento di
|H(f)|2 per due valori di
α = ±0.5, di cui a pag.
1 si trova la rappresentazione in dB oltre che la risposta di fase; questo schema
verrà inoltre ripreso al §
20.3.3 come modello della presenza di
una eco tra sorgente e destinatario.
Prima di approfondire due applicazioni del filtro, notiamo che nell’intervallo |f| < 1 2T la |H(f)|2 può comportarsi sia da passa-basso che da passa-alto, in funzione del segno di α.
Ponendo
α = − 1 nella
(10.99) si ottiene un
differenziatore numerico, dato che in tal caso la sequenza di uscita
yn = xn − xn − 1 rappresenta la
differenza finita di quella di ingresso. Nel caso tempo-continuo se oltre a porre
α = − 1, il valore di
T diviene piccolo al punto da poter considerare
T → 0,
h(t) inizia ad approssimare
un doppietto (§
99), e dunque (a parte un fattore di scala) l’uscita
è proprio la derivata dell’ingresso.
Sempre nel caso
α = − 1 e con un segnale di ingresso tempo-continuo con banda
W ≫ 1⁄T il filtro è in grado di rimuovere una
componente periodica di periodo
T, poiché in tal caso
|H(f)|2 = 0 con
f = n⁄T, in corrispondenza delle armoniche. Un filtro del genere è detto
filtro a pettine o
comb filter.
Esempio Un segnale vocale viene acquisito su di un elicottero e presenta un forte disturbo additivo periodico legato al rumore del motore e delle pale, che si desidera eliminare adottando un filtro a pettine, implementato come un fir del primo ordine.
- Considerando un regime di crociera di 300 giri/minuto, determinare l’espressione della risposta impulsiva del filtro;
- volendo implementare il filtro per via numerica, e considerando una frequenza di campionamento di 16 KHz e campioni quantizzati a 16 bit, valutare la memoria in Kbyte necessaria a realizzare il filtro.
Risposta 300 giri/min equivalgono a 300⁄60 = 5 giri/sec, ovvero ad una fondamentale di 5 Hz, ed un ritardo del filtro pari a T = 1⁄5 = 200 msec.
- Per ottenere |H(f)|2 = 1 + α2 + 2αcos2πfT = 0 per f = nT occorre porre α = − 1 , dunque deve risultare h(t) = δ(t) − δ(t − 0.2);
- l’implementazione numerica del filtro consiste nel sottrarre ad ogni campione di ingresso quello pervenuto 200 msec prima, e dunque occorre adottare un buffer circolare con memoria sufficiente ad accogliere
fc[ campioni sec ] ⋅ T[sec] = 16 ⋅ 103 ⋅0.2 = 3200
campioni. Essendo infine necessari due byte per memorizzare i 16 bit di ogni campione, occorrono 6400 bytes.
5.2.4 Filtro a risposta impulsiva infinita (IIR) del primo ordine
La caratteristica più importante che differenzia lo schema di calcolo disegnato appresso da quello precedente è la presenza di un
feedback all’indietro, per cui il valore in uscita dipende, oltre che dall’ingresso, anche dalle
uscite precedenti. Per questo motivo la
corrispondente risposta impulsiva (graficata a lato per i casi
α≶0) ha una
durata infinita, ed è pari a
Applicando le consuete regole di trasformazione otteniamo l’espressione della risposta in frequenza come
H(f) = ∑∞n = 0αne −j2πfnT che fortunatamente converge ad una espressione più compatta, grazie all’utilizzo del risultato noto per la serie geometrica
∑∞n = 0 βn = 1 1 − β con
|β| < 1, che permette di scrivere
Nel caso in cui
|α| > 1 il filtro diviene
instabile, dato che qualunque disturbo infinitesimo in ingresso produce una uscita che via via si amplifica in modo esponenziale. Per ciò che riguarda il guadagno di potenza
|H(f)|2, passaggi simili a quelli della nota
216 portano ad ottenere
|H(f)|2 = 1 (1 − αcos2πfT)2 + (αsin2πfT)2 = 1 1 + α2 − 2αcos2πfT
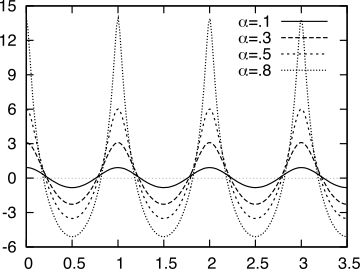
In fig.
5.14 è mostrato l’andamento del guadagno di potenza in decibel, ovvero
10 log10|H(f)|2, calcolato per
T = 1 e diversi valori di
α, positivi e negativi. Osserviamo che solo con
0 < α < 1 si può realizzare un passa-basso, e solo con
− 1 < α < 0 un passa-alto. Notiamo inoltre che più
|α| si avvicina ad uno, e più aumenta il divario tra il guadagno in banda passante e quello in banda attenuata (circa 20 dB per
|α| = .8), riuscendo così a realizzare un filtro
a banda stretta, detto anche
risuonatore. Osserviamo infine che il caso
α = 1 corrisponde ad avere un
integratore perfetto che ad esempio produce una rampa in uscita, se in ingresso c’è un gradino.
Media mobile esponenziale
Una variante dell’
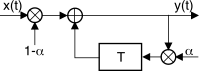
iir di primo ordine si ottiene scrivendo la relazione ingresso-uscita (vedi figura) come
a cui corrisponde una risposta impulsiva della forma
h(t) = (1 − α) ∑∞n = 0αnδ(t − nT), che ha il vantaggio rispetto alla
(10.100) di presentare guadagno unitario a frequenza zero, ovvero in presenza di un ingresso costante (a parte un transitorio) in uscita si troverà la stessa costante. Impostando
0 < α < 1 il filtro si comporta come un passa basso, e ciò permette di usare la
(10.102) per eseguire una operazione di media mobile detta
esponenziale ed ottenere valori
y depurati dalle variazioni più o meno casuali sovrapposte alla grandezza
x.
Un tipico contesto di utilizzo è nel campo dei mercati finanziari, in cui si opera su di una sequenza tempo-discreta
xn riscrivendo la
(10.102) come
yn = αyn − 1 + (1 − α)xn. La risultante sequenza
yn viene allora indicata come
ema-N, con
N che rappresenta
il numero
medio di valori precedenti su cui è operata la media. In realtà come sappiamo l’
iir opera su di una memoria infinita, ma il valore di
N serve a porre in relazione
ema-N con
sma di lunghezza
N: infatti scegliendo un valore
α = N − 1N + 1 si ottiene la stessa
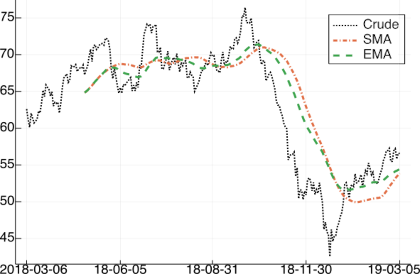
età media dei valori di ingresso utilizzati. La fig. a lato mostra il confronto tra una
sma ed una
ema a parità di
N. Dato che
ema attribuisce un peso maggiore ai valori di ingresso più recenti, viene spesso preferita alla
sma in quanto si dimostra
più reattiva alle brusche variazioni di tendenza. Infine, notiamo che qualora si scelga di porre
α = N − 1N = 1 − 1 N la
ema-
N può essere calcolata come
yn = αyn − 1 + (1 − α)xn = N − 1 N yn − 1 + 1 N xn = (N − 1)yn − 1 + xn N
.