5.3 Filtri numerici
Affrontiamo ora il tema di come passare dai concetti esposti al §
5.2 agli schemi di calcolo da adottare nel caso di una implementazione completamente numerica, associata all’elaborazione di dati campionati. Come descritto al §
5.2.2, i campioni
yk del risultato di una convoluzione
y(t) = x(t) * h(t) tra segnali limitati in banda
x(t) e
h(t) si ottengono mediante la convoluzione discreta
(10.98)
yk = T∞⎲⎳n = −∞hnxk − n
equivalente a campionare l’uscita
y(t) di un filtro trasversale con coefficienti
cn = T ⋅ hn proporzionali ai campioni
hn della risposta impulsiva
h(t) del filtro analogico di partenza. Anziché campionare l’uscita del filtro digitale, l’operazione di filtraggio viene implementata per via
hw o
sw in modo da eseguire direttamente la convoluzione discreta
yk = ∑Nn = 0 hnxk − n, come ad es. svolto dal codice
Octave mostrato sopra. Notiamo esplicitamente che nel filtraggio numerico viene omesso il fattore
T = 1⁄fc, che è inserito autonomamente dal filtro di restituzione (eq.
(10.68)) nel momento del passaggio da numerico ad analogico.
5.3.1 Sintesi FIR a partire dalla descrizione tempo continua
Acquisiamo innanzitutto due metodi per ricavare un insieme finito di coefficienti hn per il filtro numerico, a partire dalla descrizione analogica del comportamento desiderato in termini di h(t) o di H(f).
Finestratura della risposta impulsiva
In questo approccio i valori di
hn si ottengono campionando una versione
finestrata hw(t) = h(t) ⋅ w(t) della
h(t) desiderata, e quindi ritardando gli stessi al fine di ottenere un filtro causale, come discusso all’esempio di pag.
1. Come noto dal §
3.8.4, l’operazione di finestratura produce una risposta in frequenza per il filtro sintetizzato pari a
Hw(f) = H(f) * W(f), e dunque va posta particolare attenzione nella scelta della funzione finestra
w(t).
Oscillazione uniforme in frequenza
E’ una tecnica iterativa volta a rendere
minimo il massimo errore di approssimazione tra l’andamento desiderato per
|H(f)|, espresso nella forma di uno schema di tolleranza (vedi pag.
1), e l’andamento ottenibile esprimendo
|H(f)| come una combinazione di polinomi di Chebyshev. Il risultato è una
Ĥ(f) che presenta oscillazioni ridotte ma a tutte le frequenze, mentre i coefficienti
hn si ottengono mediante
dft inversa (§
4.5) della sequenza
Hn ottenuta campionando
Ĥ(f).
5.3.2 Trasformata zeta e filtraggio
Al §
4.5.1 abbiamo già discusso come una sequenza di campioni
xn = x(t)|t = nT di un segnale limitato in banda
W = 12T possa essere descritta dalla sua
trasformata zeta
X(z) = Z{xn} = ⎲⎳∞n = −∞xn z− n
e come calcolando quest’ultima per
z = e jω si ottenga una rappresentazione spettrale
X(e jω) = X(z)|z = e jω = ⎲⎳∞n = −∞xn e− jωn
di
{xn} che corrisponde alla periodizzazione della
X(f) = F {x(t)}, in cui l’intervallo di frequenze
− fc⁄2 < f < fc⁄2 si mappa in quello
− π < ω < π, ovvero
f = ω2πT.
Allo stesso modo si possono definire le trasformate zeta della sequenza di uscita da un filtro
Y(z) = Z{yn} e dei campioni della risposta impulsiva
H(z) = Z{hn} del filtro stesso, e dato che anche ora vale la corrispondenza tra convoluzione nel tempo e prodotto delle trasformate, si può scrivere
in cui
H(z) è l’analogo della
H(s) (eq.
(10.90)) tempo-continuo e per questo prende il nome di
funzione di trasferimento tempo-discreto. Sostituendo
z = e jω si ottiene la
risposta in frequenza tempo-discreto
(10.81) H(e jω) = ∑∞n = −∞hn e− jωn periodica in
ω con periodo
2π, relativa alla sequenza risposta impulsiva
hn, e che corrisponde alla
dtft (§
4.4) H•(f) = ∑∞n = −∞hn e −j2πfnT della stessa sequenza
hn qualora si ponga
ω = 2πfT, vedi anche la fig.
4.30 a pag.
1.
5.3.2.1 Filtri a risposta impulsiva finita
Affrontiamo la descrizione di un filtro
fir mediante la trasformata zeta rifacendoci dapprima al caso del filtro del primo ordine (§
5.2.3) descritto da una
h(t) = δ(t) + αδ(t − T), e consideriamo al suo ingresso una
sequenza impulsiva δn = ⎧⎨⎩ 1 n = 0 0 n ≠ 0 al posto dell’impulso di Dirac
δ(t). Il filtro è ora caratterizzato nei termini della
sequenza di risposta all’impulso hn = δn + αδn − 1 la cui trasformata zeta risulta
Allo schema computazionale di pag.
1 si affianca quindi quello
algoritmico mostrato a lato, in cui il blocco
z−1 rappresenta il ritardo di un campione, mentre il prodotto per
α è ora raffigurato come una etichetta posta sull’arco da cui passa la sequenza in transito, cosicché possiamo scrivere
Y(z) = X(z) + α z− 1 X(z) = (1 + αz− 1) X(z)
ossia la
(10.104) applicata alla
(10.103). Estendendo ora la trattazione ad un generico filtro
fir di ordine
N descritto da una
hn = ∑Nk = 0akδn − k otteniamo
in cui gli
N valori
cn rappresentano gli zeri (reali, od in coppie complesse coniugate) di
H(z).
Esercizio: media mobile E’ il filtro numerico definito a pag.
1 come un
rect discreto, ovvero con
hn = 1 per
n = 0, 1, ⋯, N − 1 e zero altrimenti.
Tenendo conto che
∑N− 1n = 0 an = 1 − aN 1 − a (), si ottiene
HMA(z) = ∑N− 1n = 0z−n = 1 − z−N 1 − z−1
che calcolata per
z = e jω fornisce
HMA(ω) = 1 − e −jωN 1 − e −jω = e −jωN⁄2 e −jω⁄2 ⋅ e jωN⁄2 − e −jωN⁄2 e jω⁄2 − e −jω⁄2 = e −jω(N − 1)⁄2 sin(ωN⁄2) sin(ω⁄2)
di cui il primo fattore è un termine di fase lineare mentre dal secondo se ne ricava il modulo
|HMA(ω)| = |||sin(ωN⁄2) sin(ω⁄2) |||
rappresentato in figura per N = 7, e che si dimostra periodico, con sei zeri equidistribuiti nell’intervallo 0 < ω < 2π. Infatti dall’espressione di H(z) = 1 − z−N 1 − z−1 si ottengono sette zeri sul cerchio unitario in posizione cn = e j2πn⁄(N − 1) di cui il primo in z = 1 si cancella con l’unico polo nella stessa posizione.
5.3.2.2 Risposta impulsiva infinita
Partendo anche questa volta dal caso del primo ordine (§
5.2.4) notiamo che campionando l’uscita si osserva la sequenza
yn = xn + αyn − 1 da cui, trasformando ambo i membri, si ottiene
Y(z) = X(z) + αz− 1Y(z) ovvero
Y(z)(1 − αz− 1) = X(z) e dunque
H(z) = Y(z)X(z) = 1 1 − αz− 1
con un polo in
z = α. Ad un generico filtro
iir di ordine
N corrisponde una
in cui
(ak, bk) sono i coefficienti di numeratore e denominatore, e
(cn, dn) le rispettive radici. Mentre il numeratore di
(10.106) esprime la componente
fir, la presenza del denominatore che conferisce alla
H(z) poli diversi da
z = 0 determina la componente con risposta
infinita. Scrivendo infatti
(10.106) come rapporto tra polinomi
H(z) = A(z)B(z) la relazione
Y(z) = H(z)X(z) diviene
Y(z)B(z) = X(z)A(z) che, antitrasformata, dà origine all’equazione
alle differenze finite yn − ∑Nk = 1bkyn − k = ∑Mk = 0akxn − k ovvero
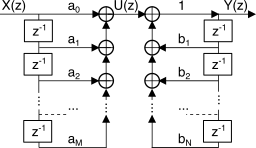
Questa espressione permette di descrivere il funzionamento del filtro in base al diagramma di fig.
5.19. Il secondo termine della
(10.107) individua la sequenza
intermedia un = ∑Mk = 0akxn − k in modo da poter scrivere
yn = ∑Nk = 1bkyn − k + un. La
forma diretta di fig.
5.19-a) altro non è che lo schema di un filtro trasversale
ruotato in verticale e che calcola
un a partire da
xn, seguito dal blocco che calcola
yn a partire da se stesso e da
un. Dato che i due blocchi esprimono relazioni lineari tempo invarianti sussiste per essi la proprietà commutativa, espressa dalla
forma canonica di fig.
5.19-b), in cui gli elementi di ritardo sono stati messi in comune, a tutto vantaggio della memoria necessaria ad implementare il filtro numerico.
I poli del denominatore della
(10.106) devono giacere tutti all’interno del cerchio unitario
|z| < 1 pena l’instabilità del filtro, sebbene siano ammessi poli con modulo unitario qualora posti in corrispondenza di uno zero, in modo da
cancellarne l’effetto.
Sensibilità alla quantizzazione
La precedente considerazione rende evidente il problema legato alla realizzazione del filtro mediante operazioni a
precisione finita: l’effetto di quantizzazione subìto dai coefficienti porta a variazioni delle posizioni di poli e zeri che possono determinare effetti indesiderati. Anche per questo motivo esistono architetture alternative a quella canonica, legate a modi di diversi di scrivere la
(10.106) come ad esempio nel prodotto di fattori, che dà luogo ad una architettura di celle in cascata.
Comportamento della fase
e complessità
Mentre per i filtri
fir esiste la possibilità di ottenere una fase lineare
(vedi pag.
1) e dunque non distorcente, per i filtri
iir questo non è possibile; d’altra parte i secondi permettono di ottenere una buona rapidità di variazione della risposta in frequenza pur mantenendo basso l’ordine, e dunque il carico computazionale.
5.3.3 Sintesi di un filtro IIR a partire da un filtro analogico
Il progetto di filtri analogici si basa su metodi consolidati ed efficienti (§
5.1), che danno luogo ad una rappresentazione nella variabile
s del tipo della
(10.90)
Ha(s) = M⎲⎳m = 0amsm N⎲⎳n = 0bnsn
a cui corrisponde una risposta impulsiva
ha(t), ed una equazione differenziale
A partire da queste grandezze sono stati individuati metodi che consentono di definire un filtro numerico
più o meno equivalente ad uno analogico, alcuni dei quali illustriamo appresso.
5.3.3.1 Invarianza della risposta impulsiva
Questo approccio ottiene i campioni
hn per il filtro numerico come
hn = ha(nT), ovvero campionando
ha(t) = F −1{Ha(f)}. Qualora
Ha(s) abbia
N poli in
s = dk, per essa sussiste le sviluppo in frazioni parziali
Ha(s) = ∑Nk = 1 Ak s − dk , a cui corrisponde una
ha(t) = ∑Nk = 1 Ak edkt e dunque una
hn = h(nT) = ⎲⎳Nk = 1 Ak edkTn
la cui trasformata zeta vale
H(z) = ⎲⎳Nk = 1 Ak 1 − edkTz−1
ovvero con poli in
z = edkT = esT|s = dk (). L’ultima osservazione comporta l’aver fatto uso della trasformazione
z = esT, che garantisce il mantenimento della stabilità.
La trasformazione
z = esT mette inoltre in corrispondenza
periodica l’asse immaginario nel piano
s (
s = jΩ = j2πf) con la circonferenza del cerchio unitario nel piano
z (
z = e jω), nel senso che ad ogni
− π < ω < π corrisponde una pulsazione
Ω = 2ω 1 2T = ω T ; pertanto la fascia del piano
s compresa tra
− fc 2 < f < fc 2 viene mappata all’interno del cerchio unitario del piano
z (vedi tab.
5.1), ed anche le fasce superiori ed inferiori subiscono la medesima sorte. Questo aspetto è una manifestazione del fenomeno
dell’aliasing che si manifesta per segnali campionati, ed avviene qualora
Ha(f) non soddisfi le condizioni di stretta limitazione in banda, rendendo il metodo idoneo solo alla progettazione di filtri passa basso o passa banda.
Un modo alternativo di vedere il problema si basa sulla considerazione che al filtro numerico corrisponde una
ĥa(t) = ∑∞n = 0hnδ(t − nT), a cui come noto (§
4.1) a sua volta corrisponde una
H•a(f) = 1T ∑∞n = −∞Ha⎛⎝f − n T ⎞⎠; dunque se
Ha(f) non è limitata in banda tra
± 12T si verifica aliasing.
5.3.3.2 Corrispondenza di poli e zeri
In questo metodo la relazione
z = esT si estende anche alla trasformazione degli zeri di
Ha(s) in quelli di
H(z): in pratica, dopo essere arrivati alla forma fattorizzata
Ha(s) = k M∏n = 1(s − cn)N∏n = 1(s − dn)
ogni zero
cn (o polo
dn) si trasforma in
ecnT (o
ednT) dando luogo a
H(z) = k M∏n = 1(z − ecnT)N∏n = 1(z − ednT) = k zM zN M∏n = 1(1 − ecnTz−1)N∏n = 1(1 − ednTz−1)
Sono mantenute le stesse corrispondenze tra piano
s e piano
z del §
5.3.3.1, così come la possibilità di aliasing. D’altra parte, i valori della risposta impulsiva
hn non corrispondono più ai campioni di
h(t).
5.3.3.3 Equazioni alle differenze
Qui si parte dalle equazioni differenziali
(10.108) che sono
a monte della
H(s), e che vengono approssimate come equazioni alle differenze finite
(10.107). Ciò porta alla equivalenza
s = 1 − z−1 T
che permette di ottenere la
H(z) a partire dalla
H(s) mediante un cambio di variabile, e che dà luogo alla corrispondenza mostrata al centro di tab.
5.1, in cui i punti dell’intero semipiano negativo del dominio
s si mappano in punti interni alla circonferenza nel piano
z di raggio
0.5 e centrata in
z = 0.5. Pertanto ora sono evitati i problemi legati all’aliasing, ma la presenza dei poli solo nel semipiano destro del piano
z impedisce l’uso del metodo per la progettazione di filtri passa-alto.
| |
|
|
|
| |
z = esT |
s = 1 − z−1 T |
s = 2 T 1 − z−1 1 + z−1 |
| |
 |
 |
 |
| |
|
|
|
Table 5.1 Aspetti peculiari delle trasformazioni H(s) ⇒ H(z)
5.3.3.4 Trasformazione bilineare
Anche quest’ultimo metodo, detto
di Tustin, trae origine dalla approssimazione numerica di una equazione differenziale, ma può essere anche visto come una approssimazione di primo ordine della relazione
z = esT analizzata in precedenza. Il metodo di Tustin si basa sul cambio di variabile
s = 2T 1 − z−1 1 + z−1
che corrisponde a mappare l’intero semipiano destro del piano
s all’interno della circonferenza di raggio unitario del piano
z, come mostrato alla destra di tab.
5.1.
Anche in questo caso il risultato è stabile e privo di aliasing; d’altra parte si verifica invece una distorsione dell’asse delle frequenze, dato che la fase ω di z = e jω è ora legata alla frequenza f del filtro analogico tramite la relazione ω = 2 arctan⎛⎝πf fc ⎞⎠ per cui va adottata una fc = 1⁄T abbastanza più elevata delle frequenze di interesse del filtro, oppure si progetta un filtro analogico che tenga conto in partenza della distorsione a cui verrà sottoposta la sua risposta in frequenza.