5.4 Filtraggio polifase
Con questo termine si indica un tipo di elaborazione numerica che comporta la variazione per un rapporto intero della frequenza di campionamento. La circostanza in cui abbiamo incontrato questa
stranezza è stata la discussione degli aspetti realizzativi del teorema del campionamento, più precisamente in relazione alle operazioni di
decimazione (§
4.2.1) ed
interpolazione (§
4.2.3), in cui un filtro numerico che approssima quanto più possibile un passa-basso
ideale con risposta in frequenza
H(f) ≃ rect2W(f) con
W pari alla massima frequenza del segnale viene rispettivamente
anteposto o posto
a valle di un elemento che rimuove od aggiunge elementi alla sequenza numerica in transito. Analizziamo ora come la realizzazione di tale filtro possa essere semplificata in modo che funzioni alla minima frequenza possibile.
5.4.1 Filtro di decimazione
Riprendiamo quanto discusso al §
4.2.1, in cui una sequenza
xn è ottenuta
sovracampionando
alla frequenza
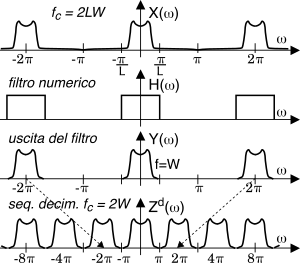
fc = 2LW un segnale
x(t) di cui si desidera limitare la banda in
± W, ma che ne occupa una pari a
± LW a causa di un filtro analogico antialiasing che per mantenere una fase lineare deve possedere una ampia regione di transizione. La sequenza
xn viene limitata nella banda
± W = ±fc 2L mediante un filtro numerico ideale
H(ω) = rect2π⁄L, che produce un nuova sequenza
yn alla stessa velocità, vedi figura a lato. I valori
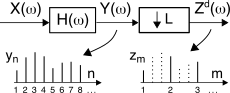
yn attraversano quindi un
decimatore con rapporto
L:1 che produce una sequenza
zdm tale che
zdm = yn = Lm,
saltando cioè
L − 1 valori ogni
L, come mostrato alla figura seguente per
L = 3.
Dopo aver notato che il decimatore è un elemento lineare, ma
non stazionario, osserviamo che per ottenere una buona approssimazione di un filtro ideale a fase lineare,
H(ω) deve essere un
fir simmetrico (pag.
1) con ordine sufficientemente elevato, che indichiamo con
N. Dunque per ogni valore di uscita il filtro deve eseguire
N + 1 prodotti ed
N somme (fig.
5.7) in un tempo
T = 12LW. Notiamo però che
L − 1 volte su
L i suoi calcoli sono
sprecati perché eliminati dal decimatore: c’è un modo per risparmiare tutto questo lavoro inutile? La risposta è positiva, vediamo come.
5.4.1.1 Decomposizione polifase
Consideriamo per primo il caso in cui la decimazione dimezzi
fc , ovvero
L = 2. La f.d.t.
H(z) = ∑∞n = −∞hnz−n del filtro descritto dai coefficienti
hn può allora essere riscritta come
in cui
E0(z) = ⎲⎳∞n = −∞ h2n z−n e E1(z) = ⎲⎳∞n = −∞ h2n + 1 z−n
sono rispettivamente le f.d.t
dei filtri con coefficienti
e0n = h2n (indici pari di
hn) e
e1n = h2n + 1 (indici dispari), chiamate congiuntamente
decomposizione bifase del filtro. Tale decomposizione è valida sia per filtri
fir che
iir, ma attualmente siamo interessati al primo caso, per il quale la fig.
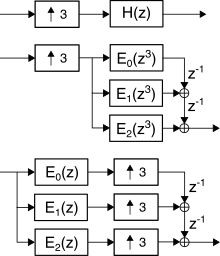
5.22 fornisce un esempio dello schema di calcolo.
La
(10.109) individua per il filtro l’equivalenza tra il primo ed il secondo diagramma computazionale mostrati in fig.
5.23, in cui il filtro originale
H(z) si scinde nel parallelo di due filtri
E0 ed
E1, ognuno dei quali con la metà dei coefficienti di
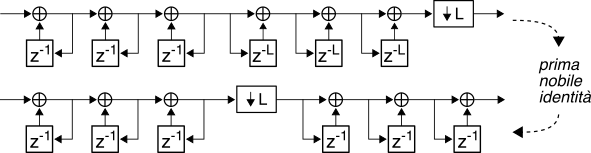
H, e con ritardi di durata doppia. Fin qui nella sostanza è cambiato poco, ma invocando la sussistenza della
prima nobile identità lo schema si può di nuovo trasformare in quello di destra, in cui il decimatore si sposta a monte dei filtri, che adesso operano a metà della velocità precedente. Notiamo che il passaggio dell’argomento delle f.d.t. da
z2 a
z è solo
apparente, dato che il decimatore
raddoppia la durata di
T.
Nel caso più generale di un decimatore L:1 lo stesso ragionamento può essere ripetuto decomponendo la f.d.t H(z) nella somma di L componenti polifase, ossia nella forma H(z) = ∑L− 1k = 0 z−k Ek(zL) in cui Ek(z) è la f.d.t. della sequenza ekn = hnL + k ottenuta prelevando un elemento ogni L dalla hn di partenza. In questo modo la complessità computazionale si riduce di un fattore L dato che, seppure il numero totale di somme e prodotti resti lo stesso, il tempo a disposizione per effettuarli è L volte maggiore.
5.4.2 Filtro interpolatore
Al §
4.2.3 abbiamo discusso come, allo scopo di distanziare le repliche del segnale campionato (fig.
4.8), sia opportuno
innalzare la frequenza di campionamento
fc di un fattore
K ovvero
f’c = Kfc, e qualora
K sia sufficientemente elevato, ottenere anche il vantaggio (§
4.2.4) di ridurre la distorsione lineare legata ad un convertitore
d/a che adotta un
s&
h con impulso rettangolare.
In tale sede abbiamo però
sorvolato sul fatto che il semplice inserimento di un interpolatore
1 : K che aggiunge
K − 1 valori nulli tra ogni coppia di elementi della sequenza originaria
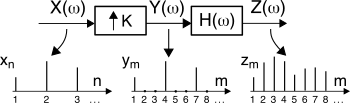
xn non risolve il problema. In realtà l’interpolatore
numerico deve
essere seguito da un filtro (anch’esso numerico) detto
filtro interpolatore, secondo lo schema mostrato in figura per il caso di
K = 3, ed il motivo è presto detto.
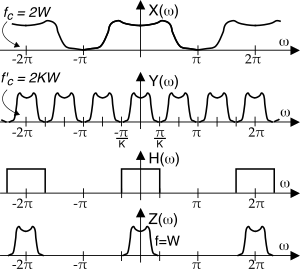
La trasformata zeta della sequenza interpolata
ym risulta
Y(z) = ⎲⎳∞m = −∞ym z−m = ⎲⎳∞m = −∞
passo K x m K z−m = ⎲⎳∞n = −∞ xn z−nK = X(zK)
in cui, essendo ym = xm⁄K se m = Kn e zero altrimenti, al terzo termine la sommatoria è valutata per m = ⋯, − 2K, − K, 0, K, 2K, ⋯, da cui il cambio di variabile.
La relazione tra i relativi spettri periodici si ottiene ponendo z = e jω e dunque possiamo scrivere Y(e jω) = X(e jKω) ovvero si assiste ad una compressione dell’asse delle frequenze di un fattore K, come rappresentato nella seconda riga della figura a lato. Ciò posto, per ottenere la sequenza zm smussata (cioè senza gli zeri in mezzo) e che rappresenta i campioni di un segnale limitato in banda ± W occorre elaborare ym mediante il filtro interpolatore H(ω) mostrato alla terza riga.
5.4.2.1 Semplificazione polifase
Lo schema precedente mostra come
H(ω) debba lavorare a frequenza
f’c = 2KW pur dovendo elaborare un segnale limitato nella banda
± W, e dunque ci chiediamo se non vi sia un modo per ridurne il carico computazionale come già avvenuto al §
5.4.1.1 per il caso della decimazione.
Il questo caso il ragionamento inizia dalla considerazione che nella sequenza
ym un solo elemento ogni
K è diverso da zero, e dunque il
fir di ordine
N che implementa
H(z) effettua
K − 1 moltiplicazioni
per zero ogni
K: pertanto
H(z) può anche qui essere scomposto in
K filtri in parallelo di ordine ridotto, secondo l’espressione
H(z) = ∑K− 1k = 0 z−k Ek(zK) in cui
Ek(z) è la f.d.t. di un
fir con coefficienti
ekn = h2n + k.
Tali filtri operano sulla base di elementi di ritardo pari a
K⁄f’c, e solamente uno di essi (a rotazione) produce una uscita diversa da zero, come rappresentato nella seconda riga della figura a lato nel caso di
K = 3, con gli elementi di ritardo
z−1 posti sulla destra che
ciclano le uscite dei filtri verso l’uscita.
A questo punto è possibile invocare l’applicabilità della seconda nobile identità che permette di scambiare la posizione dell’interpolatore numerico con quella dei filtri Ek in modo che questi possano operare alla velocità ridotta fc = 2W, riducendo anche in questo caso la complessità computazionale.
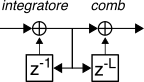
5.4.3 Filtro integratore-pettine in cascata
Il termine originale inglese è
cascaded integrator-comb o filtro di
Hogenauer (dal nome del suo ideatore) o brevemente filtro
cic,
e trova impiego negli stadi di decimazione ed interpolazione numerica, permettendo di semplificare ulteriormente la realizzazione circuitale in quanto risulta
privo di moltiplicatori, e consentendo la
programmabilità del rapporto di variazione della frequenza di campionamento; il suo uso è particolarmente vantaggioso nel caso di tassi di variazione elevati.
Questo componente (detto anche
accumulatore) implementa l’equazione alle differenze
yn = yn − 1 + xn
da cui
Y(z) = z−1 Y(z) + X(z) ed è quindi descritto da una funzione di trasferimento
HI(z) = Y(z)X(z) = 1 1 − z−1
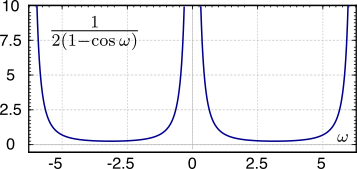
a cui corrisponde il guadagno di potenza (pag.
1)
|HI(ω)|2 = 1 2(1 − cosω) mostrato in figura: si comporta pertanto come un passa basso, presentando guadagno infinito per
ω = 0.
Come sarà chiaro tra breve, per ottenere un tasso di decimazione (od interpolazione)
L occorre impostare una equazione alle differenze
yn = xn − xn−L a cui corrisponde una f.d.t.
HC(z) = 1 − z−L
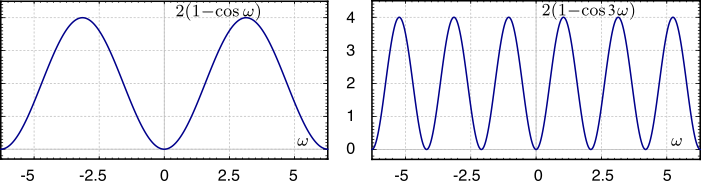
ed un guadagno di potenza
|HC(ω)|2 = 2(1 − cosLω) di cui alla figura a lato viene mostrato l’andamento per
L = 1 ed
L = 3, coerentemente con quanto ottenuto a pag.
1.
Concatenando i due filtri in cascata si realizza una funzione di trasferimento
in cui il polo in
z = 0 dell’integratore viene
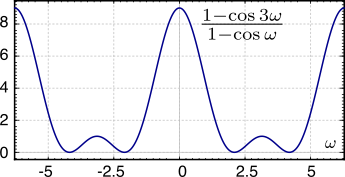
cancellato dallo zero del comb nella medesima posizione, producendo un guadagno di potenza
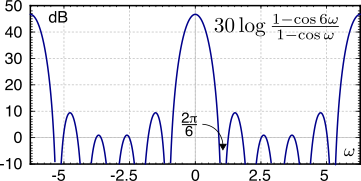
|HIC(ω)|2 = 1 − cosLω 1 − cosω mostrato in figura per
L = 3, dimostrandosi un passa basso, con zeri alle frequenze
fi = i ⋅ fc L con
i = 1, ⋯, L − 1.
Equivalente a media mobile
Ricordando nuovamente l’uguaglianza
∑N− 1n = 0 an = 1 − aN 1 − a si ottiene che la
(10.110) può essere riscritta come
HIC(z) = ⎲⎳L− 1n = 0 z−n
ossia (a meno del coefficiente
1⁄L) la f.d.t. di un filtro a
media mobile (pag.
1) con
risposta impulsiva
hn = ∑L− 1k = 0 δn − k, in quanto tale a fase lineare, e con gli stessi zeri. Evidentemente l’architettura del filtro
i&
c, mostrata a lato, costituisce una implementazione
particolarmente efficiente di un filtro a media mobile.
L’attenuazione della banda soppressa ovvero delle frequenze per cui |f| > fc L ossia |ω| > π L viene largamente migliorata qualora si pongano N celle i&c in cascata, in modo da realizzare un filtro con f.d.t.
HCIC(z) = ⎛⎝1 − z−L 1 − z−1 ⎞⎠N
e dunque con guadagno di potenza
|HCIC(ω)|2 = ⎛⎝1 − cosLω 1 − cosω ⎞⎠N
di cui la figura mostra l’andamento per
L = 6 ed
N = 3 su di una scala in dB (§
8.1).
Approfondiamo ora come quanto esposto si integri con la teoria discussa al §
5.4.1. La fig.
5.32 mostra uno schema di decimazione
L:1 realizzato mediante filtro
cic, che rientrando nel criterio di applicazione della
prima nobile identità permette di posizionare il decimatore
a monte degli elementi
comb come mostrato alla seconda riga, consentendo a questi di operare alla velocità minima. Osserviamo quindi come in questa configurazione gli elementi di ritardo risultino
indipendenti dal rapporto di decimazione
L, e dunque lo stesso schema può essere riutilizzato modificando unicamente l’elemento decimatore vero e proprio.
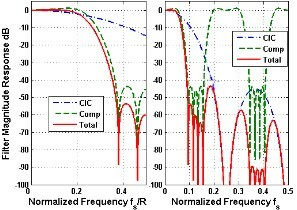
A fronte dei vantaggi discussi, l’uso di un filtro
cic presenta risvolti che richiedono una attenta progettazione. Infatti la risposta in frequenza pre-decimazione
|HCIC(ω)| = | L sin(ωL⁄2) sin(ω⁄2) |N (vedi pag.
1 per la sua derivazione) risulta essere tutt’altro che piatta nella banda passante corrispondente ad una pulsazione
|ω| = π L (o inferiore), e dunque deve essere
compensata mediante uno stadio di equalizzazione realizzato con un ulteriore filtro
fir (per mantenere la linearità di fase) di ordine elevato, e che opera alla velocità
decimata a valle dei comb, con l’effetto mostrato in fig.
5.33-a).
Lo stesso filtro di compensazione viene utilizzato anche per
aumentare l’attenuazione nella banda soppressa
1L π < |ω| < 2L − 1 L π, come mostrato in fig.
5.33-b). Infatti in tale regione il filtro
cic presenta un’attenuazione di decine di dB ma non nulla, e ciò causa la manifestazione di aliasing a seguito della decimazione, con il segnale presente nelle bande
n ⋅ 2πL ± π 4 con
n = 1, 2, ⋯, L − 1 che si
ripiega sulla frequenza zero.
Un ultimo aspetto notevole è che l’elaborazione del filtro cic deve essere svolta con operazioni in virgola fissa senza segno, dato che in tal modo è garantita la cancellazione del polo dell’integratore con lo zero del comb. Non solo, occorre anche tenere conto che la dinamica del segnale aumenta sensibilmente con il numero di stadi posti in cascata, e dunque il numero di bit dei registri di calcolo deve essere dimensionato adeguatamente. Per approfondire il tema, si possono consultare i riferimenti riportati in nota.
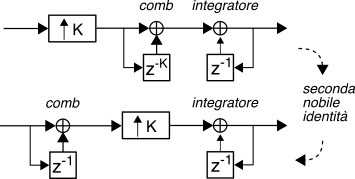
Il filtro
cic può svolgere altrettanto bene la funzione del filtro
passabasso utilizzato in uno schema di interpolazione numerica (§
5.4.2). In questo caso il
cic è nominalmente posto a valle dell’interpolatore numerico, ma scambiando tra loro di posto gli stadi comb con quelli di integrazione, è possibile applicare la seconda nobile identità per pervenire anche in questo caso ad una architettura dalla complessità computazionale minima, come mostrato alla figura precedente in cui per semplicità si è limitato ad uno il numero di stadi
i&
c.
Valgono anche in questo caso le considerazioni precedenti, ovverosia la necessità di un ulteriore filtro di compensazione della distorsione in banda passante e di attenuazione della banda soppressa, che questa volta viene posto prima dello stadio comb in modo da operare a velocità ridotta, assieme alle accortezze sulla necessaria dimensione dei registri di calcolo a virgola fissa.