6.2 Variabili aleatorie
Finora si è parlato di eventi in modo astratto, mentre spesso ci si trova ad associare ad ogni punto dello spazio campione un valore numerico: lo spazio campione Ω diventa allora l’insieme dei numeri e prende il nome di variabile aleatoria, d’ora in poi spesso abbreviato in v.a. Il verificarsi di un evento corrisponde ora all’assegnazione di un valore (tra i possibili) alla v.a.; tale valore “prescelto” prende dunque il nome di realizzazione della v.a. Distinguiamo poi tra variabili aleatorie discrete e continue, a seconda se la grandezza che descrivono abbia valori numerabili o continui. La caratterizzazione della variabile aleatoria in termini probabilistici si ottiene indicando come la “massa di probabilità” si distribuisce sull’insieme di valori che essa può assumere, per mezzo delle due funzioni (di v.a.) seguenti.
6.2.1 Densità di probabilità e funzione di distribuzione
Come la massa di un oggetto
non omogeneo è distribuita in modo più o meno denso in regioni differenti del suo volume complessivo, così la
densità di probabilità (o
d.d.p.) indica su quali valori della variabile aleatoria si concentra la probabilità. Ad esempio, la densità della v.a. discreta associata al lancio di un dado può essere scritta:
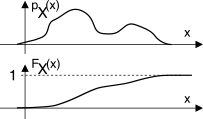
il cui significato discutiamo subito, con l’aiuto del grafico a lato, in cui
D indica la v.a. (il numero che uscirà), e
x una sua realizzazione (una delle 6 facce). I 6 impulsi centrati in
x = n rappresentano una
concentrazione di probabilità nei sei possibili valori, e l’area di tali impulsi è esattamente pari alla probabilità di ognuno dei sei risultati. E’ facile verificare che
∞⌠⌡ −∞pD(x) dx = 1 e che risulta b⌠⌡a pD(x) dx = Pr{a < D ≤ b}
ovvero pari alla probabilità che la v.a.
D assuma un valore tra
a e
b. In particolare, non potendosi verificare una probabilità negativa, si ha
pD(x) ≥ 0 con
∀x.
Una funzione di v.a. strettamente collegata alla densità è la funzione di
ripartizione o di
distribuzione, definita come
e che risulta una funzione non decrescente di
x, limitata ad un valore massimo di
1, ed il cui andamento mostriamo a lato sotto a quello di
pX(x), per la quale ovviamente risulta
pX(x) = ddx F X(x); nel caso invece della v.a. discreta
D, la relativa funzione di distribuzione è discontinua .
Ora è ancora più evidente la circostanza che pX(x) è una densità, e diviene una probabilità solo quando moltiplicata per un intervallo di x().
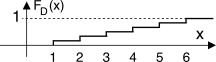
Qualora non si disponga di una espressione analitica idonea a rappresentare il modo con cui si distribuiscono i valori di una v.a., può essere utile svolgerne una stima mediante un istogramma. Questo assume l’aspetto di una versione per così dire quantizzata della d.d.p. incognita, e si ottiene a partire da una serie di realizzazioni della v.a., suddividendo il campo di variabilità della grandezza X in sotto-intervalli, e disegnandovi rettangoli verticali, ognuno di altezza pari al numero di volte che (nell’ambito del campione statistico a disposizione) X assume un valore in quell’intervallo, come rappresentato in figura.
Dividendo l’altezza di ogni rettangolo per il numero di osservazioni
N, si ottiene una approssimazione di
pX(x), via via più precisa con
N → ∞, e con una contemporanea riduzione dell’estensione degli intervalli.
6.2.2 Valore atteso, momento e momento centrato
Si tratta di grandezze per così dire
riassuntive del modo con cui si distribuiscono i valori di una v.a., e sono definite a partire da una
generica funzione di variabile aleatoria che indichiamo con
g(x).
Si definisce
valore atteso (o
media di insieme) di
g(x) rispetto alla variabile aleatoria
X la quantità
che corrisponde ad una
media pesata, in cui i valori assunti da
g(x) in corrispondenza ad un certo
x sono
pesati mediante il corrispettivo valore di probabilità
pX(x)dx; tale operazione di media integrale è indicata con la notazione
EX{.} , mediante la quale si indica a pedice la v.a. (
X) rispetto a cui eseguire la pesatura.
Nel caso di una funzione di più v.a.
g(x, y) il relativo valore atteso è calcolato in base alla d.d.p.
congiunta, ovvero
EX, Y{g(x, y)} = ∞⌠⌡ −∞∞⌠⌡ −∞g(x, y)pXY(x, y)dxdy
in cui
pXY(x, y) si ottiene a partire dalle d.d.p. condizionate e marginali, come esposto al §
6.1.3. Infine, la
(10.116) può essere calcolata utilizzando una d.p.p. condizionata
pX ⁄ Y(x ⁄ y), ed in tal caso anche il valore atteso
EX ⁄ Y{g(x)} è detto
condizionato, risultando funzione di
y.
Qualora si ponga
g(x) = xn, ovvero pari alla
n-esima potenza della v.a., il valore atteso prende il nome di
momento di ordine n, e si indica come
Nel caso di variabili aleatorie discrete, i momenti sono definiti come
m(n)X = ∑i xnipi, in cui
pi = Pr{x = xi}, pesando quindi le possibili realizzazioni
xi con le rispettive probabilità. Notiamo subito che
m(0)X = ∫∞−∞pX(x)dx = 1. Ragioniamo ora su due importanti momenti.
Valor medio e media quadratica
Il momento di
primo ordine
prende il nome di
valor medio della v.a., a volte denominato
centroide, e coincide con la
media aritmetica ottenibile a partire dalla conoscenza delle realizzazioni della v.a. ottenute ripetendo all’infinito l’esperimento aleatorio. Viceversa il momento di secondo ordine
m(2)X = ∞⌠⌡ −∞x2pX(x) dx
viene indicato come
media quadratica.
Esempio Supponiamo che la v.a.
X rappresenti l’altezza degli individui: l’altezza
media mX può essere
stimata come media aritmetica delle relative misurazioni
m̂X = N1 volte x1 + x1 + ⋯ + N2 volte x2 + x2 + ⋯ + … + Nn volte xn + xn + ⋯ N = x1N1 + x2N2 + ... + xnNn N
Al tendere di
N = ∑ni = 1Ni ad
∞, la stima
m̂X viene a coincidere con il risultato
mX fornito dalla
(10.118) qualora al posto delle probabilità
pX(x)dx si sostituiscano i valori
Pr(xi) ottenuti tramite un istogramma
Pr(xi) = N(xi < x ≤ xi + Δx)N = Ni N , tramutando così l’integrale in una sommatoria, ovvero
∫∞−∞x pX(x) dx ⇒ ∑i xi Pr(xi). Tale punto di vista motiva il senso del concetto di
pesatura dei possibili valori di
x con le rispettive frequenze.
Nel caso in cui
g(x) = (x − mX)n il relativo valore atteso è chiamato
momento centrato di ordine
n, ed indicato come
μ(n)X = E{(x − mX)n} = ∞⌠⌡ −∞(x − mX)npX(x)dx
E’ immediato constatare che
μ(0)X = 1 e che
μ(1)X = 0.
E’ il nome dato al momento centrato del 2
o ordine, corrispondente a
σ2X = μ(2)X = E{(x − mX)2} = ∞⌠⌡ −∞(x − mX)2pX(x)dx
La radice quadrata
σX della varianza
σ2X prende il nome di deviazione standard, e mentre la media
mX indica dove si colloca il “centro statistico” della densità di probabilità,
σX indica quanto le singole determinazioni della v.a. siano disperse attorno ad
mx.
Una relazione notevole che lega i primi due momenti (centrati e non) è ( ):
6.2.3 Variabile aleatoria uniforme
E’ caratterizzata dal presentare uno stesso valore di probabilità per tutto l’intervallo delle possibili realizzazioni, comprese tra un valore minimo ed uno massimo, come rappresentato in figura; pertanto la densità di probabilità è esprimibile mediante una funzione rettangolare
pX(x) = 1Δ rectΔ(x − mX)
in cui
Δ rappresenta l’estensione dell’intervallo di esistenza della variabile aleatoria, mentre il parametro
mX, che indica l’ascissa a cui è centrato il rettangolo, corrisponde esattamente al momento di primo ordine di
X. Il calcolo della varianza invece fornisce:
σ2X = Δ212.
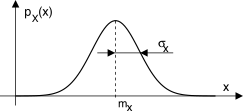
6.2.4 Variabile aleatoria gaussiana
A differenza del caso uniforme, la v.a. gaussiana presenta valori più probabili in prossimità del valor medio
mx, in accordo alla d.d.p. con espressione
ed il cui grafico dalla caratteristica forma
a campana è mostrato a lato per diversi valori dei parametri
mx e
σx che compaiono nella
(10.120), pari rispettivamente a media e deviazione standard della v.a. (vedi §
6.7.1), e che descrivono completamente la d.d.p. dal punto di vista analitico: pertanto la
stima di
mx e
σx (a partire da un buon numero di realizzazioni) è sufficiente per descrivere completamente il fenomeno aleatorio. La v.a. gaussiana emerge in molti fenomeni naturali, ed è dimostrabile analiticamente che la sua densità è tipica per grandezze ottenute dalla somma di un numero molto elevato di cause aleatorie, tutte statisticamente indipendenti e con la medesima d.d.p. (
teorema centrale del limite ).
6.2.4.1 Probabilità di un evento gaussiano
Accade che il valore dell’integrale
∫x−∞1 √2πσ e− (θ − m)2 2σ2 dθ mostrato in figura
e che corrisponde alla funzione di distribuzione
FX(x) della v.a. gaussiana
x non sia esprimibile in forma chiusa, e dunque per
FX(x) non esiste una formula precisa. Al contrario, il suo valore viene
calcolato per via numerica, e reso disponibile mediante tabelle e grafici. Per evitare di dover ripetere il calcolo per ogni possibile valore di media e varianza, l’estensione dell’area tratteggiata viene valutata per una v.a. gaussiana
normalizzata Z a media nulla e varianza
12, ed espressa nei termini della funzione
erfc{α} definita come rappresentato in fig.
6.9-a), ovvero
erfc{α} = Pr{|z| > α} = 2 ∞⌠⌡α 1 √π e− z2dz
il cui andamento è graficato in fig.
6.9-b) per i diversi valori dell’argomento
α ≥ 0.
In questi termini, la funzione di distribuzione di
z si ottiene come
FZ(z) = Pr{Z ≤ z} = ⎧⎨⎩ 1 − 1 2 erfc{z} z > 0 12 erfc{ − z} z ≤ 0
Tale risultato può quindi essere usato per calcolare il valore di probabilità
Pr{X > β} con cui una v.a.
X con media
m e varianza
σ2 supera una soglia
β ≥ m, applicando il cambio di variabile
z = x − m√ 2 σ, che fornisce
Esempio Valutare la probabilità che una v.a. gaussiana
X con
m = 2 e
σ2 = 4 superi il valore
x = 2.5. Il cambio di variabile
x − m √2σ determina per la v.a. normalizzata il nuovo valore di soglia
2.5 − 21.41 ⋅ 2 ≃ 0.17, e dalla fig.
6.9-b) si ottiene
Pr{X > β} = 12 erfc{0.17} ≃ 12 0.82 = 0.41.
Ma proviamo a svolgere i calcoli: il valore di probabilità richiesto dall’esercizio corrisponde a
Pr{X > β} = ∫∞x1 √2πσ e− (θ − m)2 2σ2 dθ; ponendo
θ − m√2 σ = η risulta
dθ = √2 σ dη mentre l’estremo inferiore di integrazione diviene
η = x − m√2 σ, ottenendo così
Pr{X > β} = ∞⌠⌡x − m √2 σ 1 √2πσ e− η2√2σ ⋅ dη = ∞⌠⌡ x − m √2 σ 1 √π e− η2dη = 1 2 erfc⎧⎩x − m √2σ ⎫⎭
Questo risultato tornerà utile al §
15.4, quando dovremo valutare la probabilità di errore nelle trasmissioni numeriche.
Alcuni esprimono la probabilità di evento gaussiano come Q{x} = Pr{X > x} = ∫∞x 1 √2π e− θ2 2 dθ, riferita dunque ad una sola coda di una v.a. gaussiana a media nulla e varianza unitaria. Tra le due notazioni sussiste pertanto la relazione Q{x} = 12 erfc⎧⎩x √2 ⎫⎭.
Per avere una idea della rapidità di azzeramento della campana gaussiana, può essere utile tenere conto che in un intervallo di estensione
2σ centrato attorno alla media si trova il 68,3% della probabilità, che sale al 95,5% per un intervallo che si estende per
±2σ attorno alla media, ed arriva al 99,7% per un intervallo
±3σ. Vedi anche la tabella a pag.
1.
Mentre ai §§
6.5 e
6.7.1 sono approfonditi ulteriori aspetti della v.a. gaussiana, altri tipi di v.a. sono descritti assieme ai rispettivi casi di utilizzo, come nel caso della v.a. esponenziale §
22.2.1, di Bernoulli §
22.1, Poisson §
22.2, Rayleigh e Rice pag.
1. Qui invece il capitolo prosegue introducendo una descrizione di v.a.
complementare a quella fornita da d.d.p. e distribuzione, mediante la quale dimostrare il comportamento di una somma di v.a. indipendenti.
6.2.5 Funzione caratteristica
La funzione caratteristica
ΦX(ω) di una v.a.
X è definita come l’antitrasformata di Fourier della sua densità di probabilità, ovvero (equivalentemente) come il valore atteso di
e jωx:
Intuitivamente, possiamo pensare che si sia scelta l’anti-trasformata anziché la trasformata in quanto una d.d.p. è una
densità (di probabilità), similmente ad una densità
spettrale. Tra una d.d.p.
pX(x) e la relativa
ΦX(ω) intercorre una relazione
biunivoca, nel senso che se due d.d.p. hanno la stessa
ΦX(ω), esse coincidono. Affrontiamo subito due importanti applicazioni di questo nuovo strumento.
6.2.5.1 Densità di probabilità della somma di v.a. indipendenti
Osserviamo che, se
z = x + y è la somma di v.a.
indipendenti, per la sua funzione caratteristica si ottiene
Φz(t) = EZ{e j(x + y)t} = EZ{ejxt ejyt} = EX{ejxt} EY{ejyt} = Φx(t) Φy(t)
in quanto sotto tale ipotesi la d.d.p. congiunta
pXY(x, y) si fattorizza nel prodotto delle d.d.p. marginali
pX(x) e
pY(y) (vedi §
6.1.5), ed il valore atteso si scompone nel prodotto di due integrali. Pertanto, la funzione caratteristica di una somma di v.a. indipendenti è pari al prodotto delle funzioni caratteristiche.
Effettuando ora l’operazione inversa (trasformata di Fourier della funzione caratteristica della somma), e ricordando che ad un prodotto in un dominio corrisponde una convoluzione nell’altro, si ottiene il risultato
pZ(z) = F {Φz(t)} = F {Φx(t)Φy(t)} = pX(x) * pY(y)
che ci permette di enunciare:
La densità di probabilità della somma di v.a. indipendenti è pari alla convoluzione tra le rispettive densità di probabilità marginali.
Esempio Se x ed y sono due v.a. a distribuzione uniforme tra ±Δ, la loro somma ha densità di probabilità triangolare con base 2Δ. Pertanto, nel lancio di 2 dadi il risultato più probabile è 7. Infatti può essere ottenuto come 6+1, 5+2, 4+3, 3+4, 2+5, 1+6, ovvero in 6 modi diversi, ognuno con probabilità 16 ⋅ 1 6 = 1 36 e dunque Pr{7} = 6 1 36 = 1 6 .
6.2.5.2 Funzione caratteristica di una v.a. gaussiana
Consideriamo il caso di una v.a. gaussiana a valor medio nullo e varianza
σ2: si tratta di eseguire il calcolo
Φx(ω) = ∫∞−∞ 1 √2πσ e− x2 2σ2 e jωx dx, il cui svolgimento porta al risultato
ovvero ancora un andamento gaussiano, con dispersione (varianza) inversamente proporzionale a quella della gaussiana di partenza. Qualora la v.a. abbia invece valore medio
mx ≠ 0 la proprietà di traslazione della
F − trasformata fornisce
Φx(ω) = e− 1 2 ω2σ2⋅ e jωmx.
Ma per non farci mancare nulla, citiamo ulteriori proprietà della funzione caratteristica:
Osserviamo che
|ΦX(ω)| = |EX{ e jωx}| ≤ EX{| e jωx|} = ⌠⌡pX(x)dx = ΦX(ω)|ω = 0 = 1
dunque
ΦX(ω) ha un massimo nell’origine.
Se
ΦX(ω) è derivabile
k volte, dalla
(10.122) si ottiene
dkΦX(ω) dωk = E{(jx)k e jωx} che calcolata per
ω = 0 fornisce
dkΦX(ω) dωk ||ω = 0 = jkE{xk} = jkm(k)x
Pertanto conoscendo i primi
n momenti
m(1)x, m(2)x, ⋯m(n)x della v.a.
x è possibile ottenere una approssimazione
Φ̂X(ω) della relativa funzione caratteristica
ΦX(ω) nella forma di una espansione in serie di potenze, ovvero
ΦX(ω) ≃ n⎲⎳k = 0 dkΦX(ω) dωk ||ω = 0 ωk k! = 1 +n⎲⎳k = 1m(k)x (jω)k k!
Conoscendo una stima
Φ̂X(ω) della f.c. della v.a.
x si può ottenere una approssimazione
p̂X(x) della relativa d.d.p. calcolandone la trasformata di Fourier, ovvero
p̂X(x) = 12π ⌠⌡ Φ̂X(ω) e −jωx dω
Estendiamo ora i concetti fin qui esposti al caso di v.a. vettoriali o multivariate, le cui realizzazioni corrispondono ad una
n − upla di valori.
6.2.6 Variabile aleatoria multivariata
In questo caso la v.a. rappresenta congiuntamente un intero vettore x di variabili aleatorie monodimensionali, ossia una loro collezione ordinata, in numero finito (ad es. N), in relazione o meno tra loro in base a legami di tipo probabilistico.
Indicando con
X la v.a. vettoriale, e con
x una sua realizzazione costituita dalle
N componenti
x1, x2, ⋯, xN, la v.a. multivariata è descritta per mezzo della d.d.p.
pX(x) = pX(x1, x2, ⋯, xN) funzione di
N variabili, per la quale deve risultare
∞⌠⌡ −∞∞⌠⌡ −∞⋯∞⌠⌡ −∞pX(x1, x2, ⋯, xN) dx1dx2⋯dxN = 1
Anche nel caso multivariato può essere definita una funzione di distribuzione
FX(x), anch’essa
N − dimensionale, il cui valore
FX(x) = Pr{x ≤ x} nel punto
x = (x1, x2, ⋯, xN) si calcola come
FX(x) = x1⌠⌡ −∞x2⌠⌡ −∞⋯xN⌠⌡ −∞pX(x1, x2, ⋯, xN) dx1dx2⋯dxN
Densità di probabilità marginale
La d.d.p.
marginale pXi(xi) della singola v.a.
monodimensionale xi che prende parte al sistema di coordinate su cui
X è definita, può essere calcolata a partire dalla d.d.p.
congiunta pX(x) mediante
saturazione delle altre v.a., ovvero
Densità di probabilità condizionata
La d.d.p. di un sotto-gruppo di v.a.
xa = (x1, x2, ⋯, xa), qualora il valore delle restanti coordinate
xb = (xa + 1, xa + 2, ⋯, xN) di
x sia da ritenersi noto, si ottiene dividendo la d.d.p. congiunta
pX(x) per quella marginale
pX(xb) che descrive gli eventi condizionanti, ovvero
pX(xa ⁄ xb) = pX(x)pX(xb)
in cui
pX(xb) è ottenuta per saturazione
(10.124). La separazione
ordinale tra i due gruppi di variabili ha lo scopo di semplificare la notazione di questa definizione; in realtà, le v.a. dei due gruppi possono essere prese con un ordine qualsiasi.
Nel caso in cui si tratti del valore atteso di una funzione di una sola v.a. marginale, si utilizza ancora la
(10.116) in cui la d.d.p. è quella marginale
pXi(xi) relativa alla v.a. rispetto alla quale si sta eseguendo la media di insieme. Per questa via è possibile ottenere un vettore
mX = (mx1, mx2, , ⋯, mxN) che rappresenta il valor medio della v.a. multivariata
X, le cui componenti
mxi sono i momenti di primo ordine delle v.a. marginali, ovvero
mxi = EX{xi} = ⌠⌡xipXi(xi)dxi
Notiamo che sebbene la notazione
EX{xi} indichi un valore atteso calcolato rispetto alla variabilità di tutte le componenti della v.a. multivariata
X, il calcolo è svolto ricorrendo alla d.d.p. marginale, in quanto le altre v.a.
xj con
j ≠ i saturano (10.124).
D’altra parte, è possibile ora valutare anche i cosiddetti momenti
misti,
in cui cioè la media di insieme considera tutti i possibili valori di due o più componenti di
X, pesando ognuno di questi con il relativo valore di probabilità. Ad esempio, un momento misto di ordine
(n, m) è definito come
m(n, m)xixj = EX{xnixmj} = ⌠⌡⌠⌡xnixmjpXiXj(xi, xj)dxidxj
ed un momento misto
centrato di ordine
(n, m) come
μ(n, m)xixj = EX{(xi − mxi)n(xj − mxj)m} = ⌠⌡⌠⌡(xi − mxi)n(xj − mxj)mpXiXj(xi, xj)dxidxj
in cui la
pXiXj(xi, xj) bidimensionale è ottenuta saturando la
pX(x) sulle dimensioni diverse da
i e
j.
E’ ora il turno di estendere i concetti probabilistici allo spazio dei segnali.