8.2 Distorsione lineare
Individua il peggioramento subito dal segnale
x(t) a seguito dell’attraversamento di un sistema lineare e permanente (o filtro, pag.
1) che
non è un canale perfetto: verifichiamo dunque innanzitutto che, in presenza di un canale perfetto,
non si verifica distorsione lineare.
In questo caso la risposta impulsiva ha la forma
h(t) = a δ(t − τ) (vedi pag.
1), e dunque per esso risulta
H(f) = |H(f)|e jφh(f) = F {a δ(t − τ)} = a e − j2πfτ
ovvero
e quindi la risposta in frequenza ha modulo costante (|H(f)| = |a|) e fase lineare: osserviamo infatti che l’espressione φh(f) = − 2πfτ corrisponde a quella di una retta passante per zero e con coefficiente angolare − 2πτ, e come fatto notare a pag. 1, ciò determina che tutte le componenti frequenziali presentano lo stesso ritardo, e quindi la forma d’onda in transito non subisce deformazioni. Infatti, per un canale perfetto si ottiene
Y(f) = X(f) H(f) = X(f) ⋅ ae − j2πfτ
e dunque, antitrasformando, y(t) = ax(t − τ).
Viceversa, ad un canale
non perfetto corrisponde
|H(f)| ≠ cost, e/o
φh(f) ≠ − 2πfτ, e dunque
y(t) non è la copia ritardata di
x(t). In questo caso il segnale di uscita viene detto affetto da
distorsione lineare e per esso si riscontra una
modifica della forma d’onda, dato che le componenti frequenziali del segnale di uscita
Y(f) = |Y(f)|e jφy(f) in cui ⎧⎨⎩ |Y(f)| = |X(f)||H(f)| φy(f) = φx(f) + φh(f)
dipendono oltre che da quelle di ingresso, anche dai valori di
H(f), come descritto a pag.
1. La distorsione risultante è detta
lineare in quanto risultato di una operazione
lineare come è la convoluzione, alla quale si applica il principio di
sovrapposizione degli effetti, e dunque la distorsione risultato di una combinazione di cause è la combinazione dei singoli effetti.
Se consideriamo segnali a banda limitata le condizioni per l’assenza di distorsione lineare sono un po’ meno stringenti, dato che in tal caso le
(10.204) devono essere soddisfatte solamente nella regione di frequenza individuata dalla banda di segnale, mentre laddove il segnale è assente, il filtro può avere risposta in frequenza qualsiasi.
In linea di principio consiste nel passaggio di un segnale
y(t) affetto da distorsione lineare attraverso un filtro (di
equalizzazione) con risposta in frequenza
G(f) = 1⁄H(f), in modo da ottenere di nuovo il segnale originario
x(t),
invertendo l’effetto della distorsione lineare - a patto di riuscire a sintetizzare il filtro
G(f)! L’argomento è trattato ai §§
13.1.1 per le trasmissioni modulate,
15.3 per quelle in banda base, e
18.4 per gli approcci
adattativi nel caso di modulazione numerica.
Distorsione di ampiezza e di fase
Osserviamo infine che, risultando
|Y(f)| = |X(f)| ⋅ |H(f)| e φy(f) = φx(f) + φh(f)
è possibile descrivere il fenomeno della distorsione lineare considerando separatamente il modulo
|H(f)| e la fase
φh(f) della risposta in frequenza, adottando quindi per esse delle rappresentazioni particolarmente utili a descrivere in modo sommario l’entità delle distorsioni stesse.
8.2.1 Distorsione di ampiezza
Misura in modo approssimato l’entità della distorsione lineare limitandosi a considerare quella legata allo spettro
di ampiezza. A questo scopo la definizione di misura in
deciBel introdotta al §
8.1 viene applicata al guadagno di potenza (pag.
1)
|H(f)|2, definendo in questo modo il
Guadagno di potenza in dB
Espresso da
consente di apprezzare il reale andamento di
|H(f)|2 anche per valori molto piccoli. Ad esempio l’applicazione di
(10.205) alla
|H(f)| di un filtro passa basso produce un
risultato simile a quello mostrato a lato, in cui alla
frequenza di taglio fT (pag.
1) per cui
|H(fT)|2 = 12|HMax|2 corrisponde un valore di
3 dB inferiore al massimo, che per un passa basso si trova nell’origine: per questo alla
fT viene dato nome di
banda a 3 dB, intendendo con questo che la potenza delle componenti frequenziali del segnale che rientrano in tale banda subirà al massimo un dimezzamento. Qualora invece il segnale in transito occupi una banda maggiore, ad es.
W, il valore di
GMaxdB − GdB(f)|f = W costituisce una misura della
distorsione di ampiezza subita dal segnale, ovvero la differenza di guadagno tra le sue componenti frequenziali più (e meno) attenuate.
Infine, qualora si desideri che la massima distorsione di ampiezza non sia maggiore di una quantità preassegnata, mediante il grafico si individua la banda entro la quale GdB(f) si mantiene all’interno della massima variazione (in dB) prevista, ottenendo così il valore della banda di segnale per cui la distorsione non supera quella desiderata.
8.2.2 Distorsione di fase
Consideriamo ora un canale privo di distorsione di ampiezza, descritto da una risposta in frequenza
H(f) = e jφ(f), con
φ(f) ≠ − 2πfτ. In tal caso il segnale in uscita subisce alterazioni della
forma d’onda, a causa del diverso ritardo subito dalle frequenze in esso presenti, come già illustrato nell’esempio di pag.
1; tale alterazione può anche produrre una notevole variazione della dinamica del segnale, nel caso in cui i diversi ritardi producano un
somma coerente delle frequenze presenti.
Per illustrare questo concetto, poniamo
x(t) = cos(2πf0t) in ingresso al canale e consideriamo assente la distorsione di modulo: l’uscita sarà allora pari a
y(t) = cos ( 2πf0t + φ(f0) ) = cos ⎛⎝ 2πf0⎛⎝t + φ(f0)2πf0⎞⎠ ⎞⎠ = = cos ( 2πf0(t − τf(f0)) )
in cui
è indicato come
ritardo di fase e misura il
tempo che intercorre tra ingresso ed uscita per una specifica frequenza
f. E’ immediato verificare che, nel caso in cui
φ(f) = − 2πfτ, si ottiene
τf(f) = τ, ovvero il ritardo è lo stesso a qualsiasi frequenza. Viceversa se
τf dipende da
f in modo
non lineare, un segnale di ingresso costituito da due o più frequenze (come le armoniche di un segnale periodico) subisce per ognuna di esse un ritardo differente, ed il segnale uscente
y(t) manifesta una
deformazione della forma d’onda.
Nel caso più generale di un segnale dallo
spettro continuo, l’analisi viene svolta scomponendo la banda del segnale in piccole regioni di frequenza, per ognuna delle quali il tempo di attraversamento del filtro è espresso dal
ritardo di gruppo pari a
in cui
f corrisponde al
centro della regione (o
gruppo) di frequenze, e
τg(f) tiene conto della
inclinazione di
φ(f) per ogni
f: i diversi valori di
τg nella banda di segnale danno quindi una
misura della dispersione temporale subita dai diversi
gruppi di frequenze presenti nel segnale. Anche per questo caso, se
φ(f) = − 2πfτ allora
τg(f) = τf(f) = τ è costante, e non si verifica distorsione di fase.
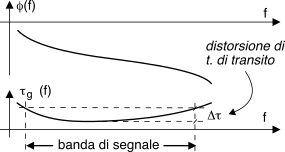
Prendiamo ad esempio l’andamento di
τg(f) mostrato in figura, e poniamo che in ingresso al filtro sia presente un suono percussivo, di breve durata e quindi esteso in frequenza. Mentre le frequenze nella regione centrale della banda subiscono un ritardo tra loro simile, quelle agli estremi arrivano con un ritardo maggiore, causandone la
dispersione temporale che snaturerà la qualità del suono. Per questo, la differenza
Δτg = τmaxg − τming viene presa come misura dell’entità della
distorsione di tempo di transito.
Il filtro trasversale in figura rappresenta un collegamento radio
in cui si verifica una eco dovuta a riflessione (vedi 20.3.3 . Per esso il guadagno di potenza e la risposta di fase risultano pari a
|H(f)|2 = 1 + a2 + 2 a cos2πfT e φ(f) = arctan − a sin2πfT 1 + a cos2πfT
e dunque è presente sia distorsione di ampiezza che di fase. Come noto H(f) è periodica con periodo f = 1 T,
dunque lo sono il modulo, la fase, e τg, mostrati tutti in figura, per α = .8 e T = 1. In base ad |H(f)|2dB viene individuata la banda a 3 dB, entro la quale la fase si mantiene abbastanza lineare, e τg varia relativamente poco. Viceversa, in corrispondenza delle regioni attenuate sono evidenti rapide variazioni di φ e τg.
Può destare legittima sorpresa osservare regioni di frequenza per le quali τg < 0, che sembrerebbero indicare una violazione del principio di causalità. Al § 13.4.1 si mostra come la (10.207) si ottenga grazie ad una approssimazione che arresta uno sviluppo in serie di potenze al primo termine, ma che nel caso in cui |H(f)| non sia costante e/o la fase cambi rapidamente pendenza non è più lecita: pertanto si tratta solo di una inesattezza del modello analitico, e l’anticausalità è solo apparente. D’altra parte, alcuni esperimenti mostrano che qualora τg < 0, il filtro assume un comportamento predittivo.
Può essere interessante chiedersi se esistano delle condizioni
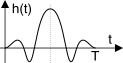
sufficienti ad assicurare che un filtro presenti risposta di fase lineare. La risposta è positiva, e la condizione è che la risposta impulsiva esibisca
simmetria pari rispetto a
metà della sua durata
T, ovvero
h(t)|0 < t < T⁄2 = h(T − t)|0 < t < T⁄2, come esemplificato in figura. Infatti in tal caso considerando un secondo filtro con risposta impulsiva
g(t) = h(t + T⁄2) ottenuta anticipando
h(t) di metà durata,
g(t) ha simmetria
pari rispetto a
t = 0, e dunque ad esso corrisponde ad una
G(f) reale (vedi pag.
1): invertendo ora la traslazione temporale operata sulla risposta impulsiva, otteniamo che
H(f) = G(f)e −j2πfT 2, ossia una fase lineare
φ(f) = − πfT. La condizione esposta è facilmente realizzabile mediante un
filtro trasversale, vedi §
5.2.1.
In effetti è possibile ottenere un ritardo di gruppo
τg(f) (10.207) costante anche qualora nella risposta di fase sia presente un termine additivo, ovvero
φ(f) = − 2πfT − θ; in particolare nel caso in cui
θ = π 2 ciò comporta che ad un segnale di ingresso
x(t) = cos(2πf0t) ne corrisponda (pag.
1) uno di uscita
y(t) = cos⎛⎝2πf0(t − T) − π 2⎞⎠ = sin(2πf0(t − T))
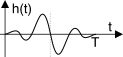
mentre si può dimostrare che in tal caso la
risposta impulsiva del filtro presenta una simmetria
dispari rispetto a metà durata, come mostrato in figura. Qualche dettaglio in più per capire meglio cosa accade viene fornito al §
13.1.2.
La linearità di fase non viene ricercata sempre e comunque, come nel caso del filtro adattato (§
7.6) in cui non è per nulla tenuta in considerazione, dato che in tal caso l’unico requisito è posto nella forma
HR(f) = G*(f)e −j2πfT in quanto lo scopo
non è preservare la forma d’onda in transito, ma calcolare l’intercorrelazione tra segnale in ingresso e risposta impulsiva adattata.
8.2.3 Effetto della distorsione lineare sui segnali
La distorsione lineare introdotta su di un segnale ad opera di un filtro produce effetti che dipendono dalla natura del segnale, e dal suo utilizzo.
Sebbene l’orecchio umano non sia sensibile allo spettro di fase per quanto riguarda i segnali periodici, come già osservato la variazione del ritardo di gruppo Δτg nella banda di segnale determina una dispersione temporale dei suoni brevi e ricchi di contenuto spettrale, e dunque la modifica del loro effetto percettivo; d’altro canto, la presenza di una distorsione di fase non altera l’intelligibilità del parlato, ma causa comunque un effetto percepibile. Viceversa, le alterazioni del modulo di H(f) modificano il timbro dei suoni, alterandone la distribuzione della potenza Py(f).
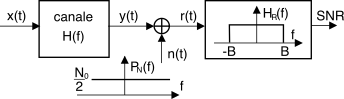
Se il segnale
y(t) viene ricevuto in presenza di disturbi additivi con densità di potenza
PN(f) = No⁄2, il ricevitore provvede innanzitutto ad eliminare le componenti di rumore esterne alla banda di segnale
B mediante un filtro passabasso
HR(f), vedi §
15.4.1.
Dato che l’attraversamento del canale con
|H(f)| ≠ cost ha modificato la densità
Py(f) del segnale ricevuto rispetto a quella di
Px(f), la valutazione dell’
SNR in ricezione deve tenere conto dell’effetto filtrante introdotto dal canale, ossia:
SNR = Py PN = ⌠⌡BPy(f)df ⌠⌡BPN(f)df = ⌠⌡BPx(f)|H(f)|2df N0B
Allo stesso tempo, l’
SNR modifica la propria dipendenza dalla frequenza, ossia
SNR(f) = Px(f)|H(f)|2N0⁄2
Sebbene i due casi che seguono non siano ancora stati esattamente definiti, sono comunque inserite qui le considerazioni riassuntive al loro riguardo.
Questo tipo di segnale è introdotto al cap.
15 e poi ripreso al cap.
16. Per esso la
linearità di fase è di fondamentale importanza allo scopo di evitare fenomeni di
interferenza intersimbolica (§
15.1.2.2), che come vedremo sono conseguenza diretta dei fenomeni di dispersione temporale, dato che questi ultimi
scombussolano le condizioni di Nyquist (§
15.2.2.2) su cui l’impulso
g(t) adottato dal codificatore di linea (§
15.1.2) è fondato.
Indicando con
x(t),
y(t) e
h(t) l’inviluppo complesso (§
11.2.1) di ingresso, uscita, e della risposta impulsiva di un canale, al §
13.1.1 si mostra che risulta
y(t) = 1 2 x(t) * h(t), e dunque per le componenti analogiche di bassa frequenza di
y(t) si manifesta un fenomeno indicato come
intermodulazione delle c. a. di b. f., che consiste nelle relazioni
Qualora
H(f) presenti simmetria coniugata rispetto ad
f0 si ottiene
hs(t) = 0, riducendo l’effetto dell’intermodulazione a quanto si otterrebbe filtrando ciascuna delle c.a. di b.f. mediante
hc(t). D’altra parte, anche quest’ultimo tipo di distorsione può essere evitato qualora
h(t) rappresenti un canale perfetto, a cui in questo caso corrisponde la condizione che, oltre a risultare
|H(f)| = cost, il ritardo di gruppo
τg(f) sia
costante nella banda di segnale, o in modo equivalente
φ(f) sia
lineare attorno alla portante
f0, cioè
φ(f) = φ0 − 2π(f − f0)τ. Ulteriori approfondimenti ai §§
13.1.2.4 e
13.2.