9.5 Codifica di sorgente con perdita di informazione
Si rende necessaria quando il canale trasmissivo non può trasportare un flusso informativo qualsiasi, ma esiste un limite RM alla massima velocità di codifica R, ovvero si impone che R ≤ RM. Ciò è possibile a patto di accettare una perdita di informazione che si traduce nell’insorgere di una distorsione D del messaggio, di cui vogliamo stabilire l’entità D(R), in funzione della velocità R. Siamo altresì interessati a stabilire il viceversa, ovvero quale sia la minima velocità di trasmissione R(D), qualora si accetti una distorsione D ≤ DM.
Messaggi di natura discreta
Quando la massima velocità
RM è inferiore al tasso informativo
(10.223) della sorgente, anche la codifica più efficiente sviluppa una velocità
R eccessiva e dunque si è obbligati a
scartare informazione, come ad esempio omettere la trasmissione di intere codeword, con la conseguenza di introdurre errori (o distorsione
D) nel messaggio codificato, in proporzione tanto maggiore quanto minore è
RM.
Qui abbiamo due strade possibili: o intraprendere un processo di campionamento e quantizzazione (§
4.3) per produrre un segnale numerico con velocità
R ≤ RM, ed incorrere in una distorsione di quantizzazione
D tanto maggiore quanto minore è la
RM consentita, oppure effettuare una trasmissione analogica del segnale
x(t) con una potenza
S, con le conseguenze
- di ricevere r(t) = x(t) + n(t), in cui il rumore n(t) di potenza N in ricezione causa una distorsione d(t) = n(t) = x(t) − r(t) di potenza D = N;
- l’entità di tale distorsione D può essere ridotta aumentando il rapporto snr = S⁄N oppure la banda del canale W, ovvero aumentandone la capacità C e di pari misura la massima intensità di informazione RM che può essere trasferita.
Nel caso continuo pertanto, sia che la sorgente venga quantizzata, sia che se ne effettui la trasmissione come segnale analogico, sussiste un legame inverso tra distorsione e velocità di trasmissione, il cui studio prende il nome di
teoria velocità-distorsione, di cui discutiamo ora.
9.5.1 La distorsione di codifica
Per individuare la relazione
R(D) tra la minima velocità
R di trasmissione di una codifica (con perdite) di una sorgente informativa e la distorsione
D che si ritiene
accettabile ci riferiamo alla figura a lato, in cui un simbolo (sorgente discreta) o valore (s. continua)
x da trasmettere viene rappresentato mediante codeword
c = f(x) di
R binit, limitando dunque l’alfabeto a
2R elementi, a cui si associa in ricezione un nuovo valore
x̂ = g(f(x)) ≠ x. La corrispondenza tra
x ed
x̂ viene quindi espressa in termini probabilistici come
p(x̂ ⁄ x), mentre indichiamo con
d(x, x̂) la misura della distorsione corrispondente. A questo punto è possibile definire la
distorsione media Dx in cui si incorre nel rappresentare un generico valore (o simbolo)
x mediante
x̂ come un valore atteso, ossia
Dx = EX̂, X{d(x̂, x)} = ∬p(x̂ ⁄ x)p(x)d(x̂, x)dx̂dx
la cui entità dipende sia dalla scelta della misura
d(x, x̂) che dalla d.d.p.
p(x̂ ⁄ x), risultato della scelta delle operazioni di codifica
c = f(x) e restituzione
x̂ = g(c).
9.5.2 Funzione velocità-distorsione
E’ il nome dato alla relazione
R(D) definita come la soluzione ad un problema di
minimizzazione, ossia come quella che rende minima l’informazione mutua media
I(x̂;x) tra
x e
x̂ al variare di
p(x̂ ⁄ x) in tutti i modi possibili, in modo da mantenere
Dx inferiore alla distorsione desiderata
D:
Ricordando le osservazioni svolte al §
9.4.3 a proposito di
I(X̂;X), questa misura quanto la conoscenza di
x̂ riduce l’incertezza a riguardo di
x, incertezza che altrimenti sarebbe pari all’entropia
H(X): intuitivamente si desidera che tale riduzione sia la massima possibile, e dunque la minimizzazione espressa dalla
(10.242) va considerata congiuntamente al vincolo
p(x̂ ⁄ x): Dx ≤ D, vincolo conseguibile purché
I(x̂;x) sia grande a sufficienza.
9.5.2.1 Shannon lower bound
Soluzioni generali per
(10.242) sono difficili da ottenere, ma si può comunque mostrare che
R(D) è continua, monotonicamente decrescente, e convessa (ossia
ad U). Sussiste inoltre un
limite inferiore valido per criteri di distorsione
d(x, x̂) di tipo errore quadratico e per sorgenti qualsiasi e senza memoria, ma che ora illustriamo per il caso continuo, e che afferma
dove
h(X) è l’entropia differenziale della sorgente, e
h(D) quella di una v.a. gaussiana con varianza
D. Per dimostrare la
(10.243) iniziamo osservando che in base alla relazione
I(X;X̂) = h(X) − h(X ⁄ X̂) (§
9.4.3) possiamo scrivere la
(10.242) come
in cui l’ultimo termine esprime l’incertezza residua su
X una volta nota la sua codifica
X̂, incertezza pari a zero qualora
X̂ = X, e dunque abbiamo
R(D)|D = 0 = h(X). Se invece
D > 0 possiamo scrivere
in cui la prima eguaglianza significa che, dopo la conoscenza di
X̂, rimane la stessa incertezza sia a riguardo del valore vero
X che a riguardo dell’errore
X − X̂; la successiva diseguaglianza deriva invece dalla constatazione che aggiungendo informazione
(X̂) l’entropia non può aumentare, e dunque
h(X − X̂ ⁄ X̂) ≤ h(X − X̂). Dato però che nella
(10.244) l’ultimo termine compare con il segno meno, sostituendovi la
(10.245) si ottiene
Per arrivare alla
(10.243) è ora sufficiente osservare che una distorsione definita come
D = E{(X − X̂)2} è a tutti gli effetti una varianza
σ2, dunque la condizione
Dx ≤ D pone un limite
σ2 ≤ D alla varianza dell’errore
X − X̂. Al §
9.3.2 si è mostrato che la sorgente che fornisce la massima entropia differenziale
h per
σ2 assegnata è gaussiana, con
h = 1 2log2(2πeσ2), e dunque
maxDx ≤ D{h(X − X̂)} ≤ 12 log2(2πeD), che sostituita nella
(10.246) fornisce la
(10.243).
9.5.3 Curva velocità-distorsione per sorgente gaussiana
Qualora la v.a. continua
x sia di tipo gaussiano, senza memoria e con varianza
σ2x, inserendo l’espressione della corrispondente entropia differenziale
(10.235) nella
(10.243) si ottiene una funzione velocità-distorsione
(10.242) pari a
RG(D) = 1 2 log2(2πeσ2x) − 1 2 log2(2πeD) = − 12 log2 Dσ2x
con il segno di uguale, ovvero la sorgente gaussiana
consegue il limite inferiore
(10.243). Osserviamo ora che per
D = σ2x si ottiene
R(D)|D = σ2x = 0 ovvero
non occorre
trasmettere nulla (
x̂ = 0), in modo che l’errore
e = x − x̂ = x abbia appunto potenza
σ2x = D. Se poi
D > σ2x ossia la distorsione
è superiore alla potenza di segnale, è sufficiente generare un valore
x̂ gaussiano, a media nulla,
indipendente da
x e di varianza
D − σ2x per ottenere una distorsione
E{(x − x̂)2} = σ2x + D − σ2x = D.
L’espressione finale per questo caso risulta dunque
Sorgente non gaussiana e confronto prestazioni
In questo caso l’entropia
h(X) è inferiore al caso gaussiano, e quindi il limite
(10.243) fornisce un valore
R(D)min
più piccolo di
(10.247),
abbassando la curva mostrata sopra. Una volta stabilito
un modello (anche sperimentale) della d.d.p. della nostra sorgente, e valutata (anche numericamente) la sua entropia, possiamo usare la
(10.243) per tracciare la relativa curva
R(D)min, e confrontare rispetto ad essa le prestazioni conseguite dal metodo di codifica che stiamo sviluppando, come esemplificato a lato.
Curva distorsione-velocità
Invertendo la relazione
(10.247) si ottiene che la
minima distorsione D conseguibile da una sorgente gaussiana in corrispondenza ad una
velocità di
R binit/campione risulta pari a
ovvero la distorsione per sorgenti gaussiane e con
R fissato è proporzionale alla varianza
σ2x, e decresce esponenzialmente con la velocità, come mostrato in figura.
Definendo il rapporto segnale-rumore in dB (§
8.1) come
10 log10 σ2xD la
(10.248) consente di ottenere
SNRdB = 10 log10 22R = 2R ⋅ 10 log10 2 = 6 ⋅ R dB
ossia un miglioramento di 6 dB per ogni binit in più utilizzato per la codifica di un campione, confermando in pieno il risultato già ricavato al §
4.3.1.1.
Il valore
(10.248) rappresenta un
limite superiore per la distorsione a velocità
R per una sorgente non gaussiana, o gaussiana ma con memoria, per la quale si possono ottenere valori di distorsione inferiori; la
(10.248) individua quindi
il più grande valore della distorsione
minima, per velocità
R e potenza
σ2x assegnate. D’altra parte è anche definito un
limite inferiore DL(R) che individua la minima distorsione sotto cui non si può scendere per un dato
R per sorgenti non gaussiane e senza memoria, in modo da poter scrivere
in cui
Q è la...
Esprime una quantità direttamente legata all’entropia differenziale della sorgente, con valore
che per sorgenti gaussiane fornisce
QG = σ2x, mentre per altri tipi di v.a. si ottiene un valore inferiore. Si può anche interpretare
Q come la varianza di una sorgente gaussiana con la stessa entropia della sorgente in esame. Sostituendo
(10.250) in (
10.249) osserviamo come il limite inferiore di distorsione
DL(R) si riduce al diminuire di
h(X), ovvero sorgenti meno informative conseguono distorsioni minori a parità di velocità.
9.5.4 Sorgente continua con memoria
Come per il caso di sorgenti discrete anche per quelle continue la dipendenza statistica tra i campioni di segnale riduce la quantità di informazione emessa, cosicché a parità di distorsione la sorgente può essere codificata a velocità ridotta, oppure a parità di velocità si può conseguire una distorsione inferiore. Anche stavolta la sorgente più difficile (ossia a cui compete la massima distorsione minima) è quella gaussiana, per la quale si ottengono risultati la cui interpretazione è molto interessante; prima di esporli conviene però fare un piccolo passo indietro.
9.5.4.1 Entropia e potenza entropica di sorgente gaussiana con memoria
Analogamente al caso discreto (§
9.2), per una sequenza (o vettore
colonna) x = (x1, x2⋯, xn)T di
n v.a. con ampiezza continua, descritte da una d.d.p. congiunta
p(x), si definisce una entropia differenziale
a blocco come
la cui valutazione è generalmente intrattabile. Se consideriamo un processo gaussiano
x(t) limitato in banda, a media nulla, stazionario e con densità di potenza
Px(f) colorata, i suoi campioni
xk = x(kTc) (cap.
4) hanno d.d.p. congiunta (§
6.5)
pX(x) = 1 √(2π)ndet(Rxx) exp⎧⎩− 12 x⊤R− 1xxx⎫⎭
dove
Rxx = E{xx⊤} è la matrice
di correlazione, simmetrica e con elementi diagonali uguali tra loro e pari a
Rxx(i, i) = E{x2} = σ2x. In tal caso la
(10.251) fornisce
hn(X) = 1 2 log2 (2πe(det(Rxx))1⁄n)
da cui, dopo aver definito l’entropia differenziale per simbolo come
h(X) = limn → ∞ hn(X), ricaviamo la potenza entropica per questo caso, pari a
(vedi §
9.6.3) dove
0 ≤ γ2x ≤ 1 è una
misura di piattezza spettrale che vale uno per un processo
bianco o senza memoria, tornando così all’espressione
Q = σ2x valida in tal caso. Viceversa
Q si riduce (
γ2x < 1) per un processo gaussiano a valori correlati, e quindi con una densità spettrale
colorata ed una maggiore
predicibilità dei suoi valori, e dunque una minore entropia.
9.5.4.2 Funzione distorsione-velocità per sorgente gaussiana con memoria
Il valore di
Q (10.252) consente il calcolo del
limite inferiore definito alla
(10.249):
Mostriamo ora in quale caso la distorsione effettiva consegue il limite ossia
DG, mem(R) = DL, G, mem(R), e quale sia il valore
DG, mem(R) > DL, G, mem(R) in caso contrario.
Le funzioni
(10.247) e
(10.248) nel caso di sorgente gaussiana con memoria, i cui campioni sono descritti da uno spettro di densità di potenza
Sxx(e jω) colorato, devono essere espresse in forma
parametrica come
in cui all’aumentare di
φ,
D aumenta ed
R diminuisce,
come andiamo a spiegare con l’aiuto della figura
9.13.
Le regioni indicate con
B, in cui
φ > Sxx(e jω), non contribuiscono al valore di
R, dato che nella
(10.254) il
log è negativo, mentre contribuiscono al valore di
D (eq.
(10.254)) solamente per l’area ombreggiata in verde, ossia nelle regioni
B la distorsione
D ha densità di potenza
colorata come
Sxx. Quando invece
Sxx(e jω) > φ (regioni
A) il contributo a
D non dipende dal valore di
Sxx(e jω) ed assume l’aspetto (aree ocra) di un rumore
bianco; viceversa (sempre in
A) il contributo ad
R è legato (con legge logaritmica) al valore delle aree lilla (indicate con
C).
Questa interpretazione grafica delle
(10.254) e
(10.254) viene denominata
a riempimento d’acqua perché simula un recipiente con la forma di
Sxx(e jω) per il quale le regioni
A fungono da
vasi comunicanti riempiti di acqua fino al livello
φ. Da tale discussione traiamo i risultati
- una volta assegnata una distorsione D la codifica ottima non spreca velocità binaria R per rappresentare regioni di frequenza (B) dove il segnale è più debole;
- la costanza delle densità spettrale dell’errore D nelle regioni A fa si che l’SNR locale migliori proporzionalmente a Sxx(e jω), densità spettrale del segnale.
Osserviamo ora che ponendo
φ > max{Sxx(e jω)} la sagoma di
Sxx(e jω) si riempie completamente d’acqua, la
(10.254) fornisce
D = σ2x, mentre la
(10.254) restituisce
R = 0; viceversa nel caso in cui
φ < min{Sxx(e jω)} ci si trova nelle condizioni di
bassa distorsione per le quali
D consegue il suo valore limite inferiore espresso dalla
(10.253), ovvero
dove
0 ≤ γ2x ≤ 1 è la misura di
piattezza spettrale già introdotta nella
(10.252). Qualora
Sxx(e jω) sia costante risulta
γ2x = 1, ri-ottenendo così il risultato
(10.248) trovato per il caso senza memoria.
Esempio Consideriamo la sequenza di tipo
autoregressivo x(n) = z(n) + α ⋅ x(n − 1) presente all’uscita di un filtro passa basso numerico
iir del primo ordine (§
5.3.2.2) con
h(n) = αn (per
n ≥ 0 ed
0 < α < 1), al cui ingresso è presente una sequenza
z(n) di campioni di un processo gaussiano, a media nulla, varianza
σ2z ed a valori indipendenti ed incorrelati da quelli di
x. Anche
x(n) sarà dunque gaussiano, ma con autocorrelazione
Rxx(k) = α|k|σ2x, varianza
σ2x = σ2z1 − α2, piattezza spettrale
γ2x = 1 − α2 e densità di potenza
colorata pari a
Sxx( e jω) = σ2z ⋅ |Hxx(e jω)|2 = σ2x1 − α2 1 + α2 − 2αcosω
All’aumentare di
α la misura di piattezza
γ2x si riduce,
x(n) diviene più predicibile, e la distorsione
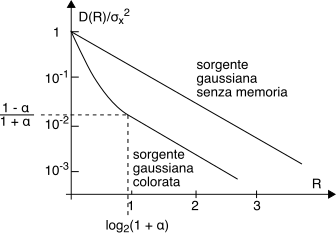
D = 2 − 2R(1 − α2)σ2x (10.253) diminuisce. Il minimo valore di
Sxx( e jω) si ottiene per
ω = π (vedi fig.
4.28 ), ed è pari a
Ponendo (ad esempio)
α = 0.95, la
(10.257) fornisce
6 ⋅ σ2x: pertanto la regione
a bassa distorsione in questo caso è definita come
D⁄σ2x ≤ 0.0256, o
R ≥ log2(1 + α) = 0.964, ed in tale regione è lecito applicare la
(10.256) ossia
D(R) = 2 − 2R(1 − α2)σ2x = 0.0975 ⋅ 2 − 2Rσ2x
avendovi sostituito i valori per
γ2x ed
α. Il risultato è la retta parallela a quella per una sorgente gaussiana senza memoria mostrata alla figura a lato, su di una scala logaritmica per le distorsioni. Per valori
D⁄σ2x > 0.0256 la distorsione
D aumenta più rapidamente ed il suo valore va determinato applicando la
(10.254), per raggiungere (ad
R = 0) il valore
σ2x, come avviene per il caso senza memoria.
9.5.4.3 Sorgente non gaussiana
In questo caso la
(10.256) si riscrive sostituendo al posto di
σ2x la potenza entropica
Q espressa dalla (
10.250) in cui il valore di entropia differenziale è ora quello della sorgente con memoria, inferiore al caso senza memoria, ottenendo così valori
D(R) ancora inferiori.
L’applicazione dei principi relativi alla codifica di sorgente al caso specifico dei messaggi multimediali (audio e video) viene trattata al capitolo
10, mentre l’applicazione dei concetti di informazione mutua media e di entropia condizionale al calcolo della capacità di canale è sviluppata al capitolo
17.