9.6 Appendici
9.6.1 Metodo dei moltiplicatori di Lagrange
Costituisce un modo di affrontare un problema di ottimizzazione vincolata, ossia individuare i punti x* di massimo o minimo (detti estremali) per una funzione obiettivo f(x) definita in un aperto A ⊂ ℝn (ossia dipendente da più variabili x = (x1, x2, ⋯xn)), nel rispetto di una o più condizioni di vincolo del tipo qi(x) = bi ossia gi(x) = 0 con i = 1, 2, ⋯, m dopo aver posto gi(x) = qi(x) − bi.
Le condizioni di vincolo individuano una regione ammissibile X per le soluzioni x* ∈ X come X = {x ∈ A: gi(x) = 0 con i = 1, 2, ⋯, m}.
Osservazione L’insieme X ha gradi di libertà ridotti rispetto all’aperto A: ad esempio se n = 2, ovvero z = f(x, y) è una superficie, allora un vincolo g(x, y) = 0 è una curva nel piano (x, y), proiezione della intersezione tra la superficie z = q(x, y) ed il piano orizzontale z = b. A sua volta la curva espressa dal vincolo g(x, y) = 0 viene proiettata in verticale sulla superficie z = f(x, y), individuando su di essa un cammino lungo il quale si trovano i punti x* di ottimo vincolato. Qualora si aggiunga un ulteriore vincolo g2(x, y) = 0 l’insieme X si riduce ulteriormente ai punti di intersezione tra i cammini disegnati sulla superficie z = f(x, y) dai due vincoli.
A patto che le funzioni siano derivabili con derivate continue e che
m < n, trovare i punti
x* estremali di
f(x) nel rispetto dei vincoli
g(x) = 0 passa per la definizione della funzione
Lagrangiana come
in cui
g(x) è il vettore delle
m funzioni
gi(x),
λ un vettore di
m moltiplicatori scalari, e
⟨λ, g(x)⟩ esprime il prodotto scalare (§
2.4.3) tra i due. Osserviamo che
L è una funzione di
n + m variabili, le dimensioni di
x e
λ.
Gradiente prima di poter proseguire occorre definire l’operatore
gradiente ∇ di
f(x) come il vettore i cui elementi ne sono le derivate parziali, ossia
∇f(x) = ⎛⎝∂f∂x1, ∂f ∂x2, ⋯, ∂f ∂xn⎞⎠. Il suo orientamento nello spazio indica la direzione verso cui
f(x) cresce più velocemente, e se
x = x0 è un
punto stazionario (minimo, massimo o di sella) di
f(x), allora
∇f(x0) = 0, ovvero piccole variazioni dell’argomento
x ≃ x0 non alterano di molto il valore di
f.
Possiamo finalmente enunciare il teorema, che afferma
Qualora esista un punto x* di ottimo vincolato, e la matrice Jacobiana J{g(x*)} abbia rango m, allora esiste un vettore λ* ∈ ℝm tale che
ovvero i valori (x*, λ*) individuano punti stazionari di (10.258)
Ciò comporta che
- l’azzeramento di ∇L(x, λ) per un qualche valore (x*, λ*) è condizione necessaria all’esistenza del punto x* di ottimo, ovvero i valori che verificano la (10.259) possono non essere soluzione al problema di ottimo, ma devono essere verificati singolarmente;
- ∇L (10.259) è un vettore i cui elementi sono n + m funzioni di x e λ, il cui azzeramento realizza un sistema di altrettante equazioni, le cui soluzioni sono i valori (x*, λ*) desiderati;
- i primi n elementi di ∇L sono le ∂L∂xj con j = 1, 2, ⋯, n, il cui azzeramento implica ∂f ∂xj = ∑mi = 1 λ * i ∂gi ∂xj ovvero ∇xf(x*) = ∑mi = 1 λ * i ∇x gi(x*) od anche ∇xf(x*) = ⟨λ*, ∇xg(x*)⟩, e cioè quando (x, λ) = (x*, λ*) il gradiente della funzione obiettivo ∇xf diviene eguale ad una combinazione lineare ∑mi = 1 λ * i ∇x gi degli m gradienti delle condizioni di vincolo, con i moltiplicatori λ * j come coefficienti. Ciò comporta che ∇xf(x*) è ortogonale a ciascun cammino individuato dai vincoli, o ovvero che la curva di livello di f(x) che passa per x = x* è tangente (in tale punto) alla curva descritta dal vincolo;
- gli ultimi m elementi di ∇L corrispondono a ∂L∂λj = − gj(x) e dunque il loro annullamento comporta il rispetto dei vincoli;
- se i vincoli sono soddisfatti il termine ∑mi = 1 λ * igi(x) della (10.258) è nullo, e dunque i punti estremali di L al variare di x lo sono anche per la f(x) di partenza;
- la condizione J{g(x*)} di rango m garantisce che i gradienti dei vincoli siano linearmente indipendenti, consentendo di trarre le conclusioni di cui al punto 3. Qualora la condizione non si verifichi la soluzione offerta dal teorema non è praticabile, dato che in tal caso ∇L può non azzerarsi nei punti di ottimo, per qualunque λ.
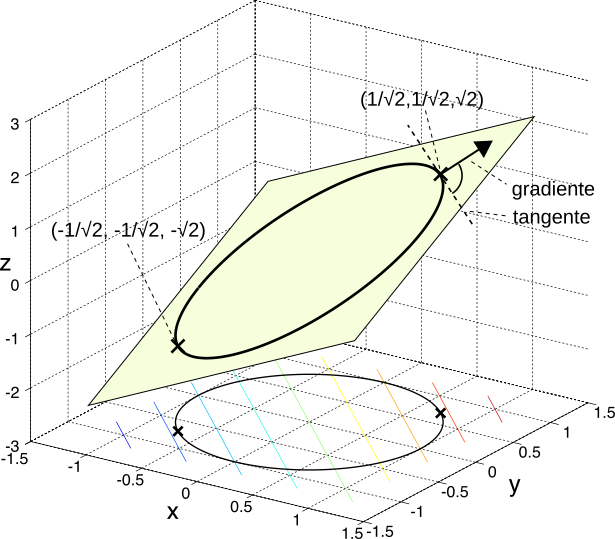
Esempio Si trovino i punti di massimo e di minimo della funzione
f(x, y) = x + y sottoposta al vincolo
g(x, y) = x2 + y2 − 1 = 0. Con l’aiuto della figura,
osserviamo che i punti devono giacere sulla intersezione tra un piano inclinato
z = x + y e la proiezione su di esso di una circonferenza di raggio unitario, risultato dell’intersezione tra un paraboloide
z = x2 + y2 ed il piano
z = 1. Per la Lagrangiana otteniamo
L(x, y, λ) = x + y − λ(x2 + y2 − 1), e l’annullamento del relativo gradiente da luogo al sistema
⎧⎪⎨⎪⎩ 2λx − 1 = 0 2λy − 1 = 0 x2 + y2 − 1 = 0 , da cui si può ottenere che
(x*, y*, λ*) = ±⎛⎝1√2, 1√2, 1√2⎞⎠. Dato che
f⎛⎝1√2, 1√2⎞⎠ = √2 e che
f⎛⎝ − 1√2, − 1√2⎞⎠ = − √2, il primo punto individua un massimo, ed il secondo un minimo, entrambi di tipo vincolato. Osserviamo come
∇f sia ovunque pari a
(1, 1), e nei punti di ottimo risulti
ortogonale alla tangente al cammino individuato dal vincolo.
9.6.2 Massimo dell’entropia per variabile aleatoria gaussiana
Si intende ora mostrare la validità della
(10.236), ovvero che l’entropia differenziale per sorgente continua gaussiana
hG = 12 log2(2πeσ2) (eq.
(10.235)) è il
massimo che si può ottenere per qualunque scelta della d.d.p. di primo ordine
p(x) della sorgente, una volta fissata la sua varianza
σ2, ossia
hG = 12 log2(2πeσ2) = maxp(x){− ⌠⌡ p(x)log2p(x)dx} dato σ2
Per arrivare allo scopo si può adottare il metodo dei moltiplicatori di Lagrange (§
9.6.1), considerando
p(x) = p come una
variabile p (anziché una funzione) rispetto a cui massimizzare, nel rispetto dei vincoli
g1(p) = ∫p(x)dx − 1 = 0 e
g2(p) = ∫ x2p(x)dx − σ2 = 0, mentre il vincolo sul valor medio è ininfluente a causa dell’invarianza evidenziata a pag.
1.
Scriviamo dunque il lagrangiano come
L(p, λ1, λ2) = − ⌠⌡p(x)log2p(x)dx − λ1(⌠⌡p(x)dx − 1) − λ2(⌠⌡x2p(x)dx − σ2x) = = − ⌠⌡[p(x)log2p(x) + λ1p(x) + λ2x2p(x)]dx + λ1 + λ2σ2x = = − 1ln 2 ⌠⌡[p(x) ln p(x) + λ1p(x) + λ2x2p(x)]dx + λ1 + λ2σ2x
in cui si è sostituito
log2p(x) = 1ln 2 ln p(x) e si adotta una eguale scalatura per i moltiplicatori
λi. Il massimo di
L(p, λ1, λ2) si ottiene eguagliandone a zero le derivate parziali, ed applicando la proprietà di
derivata sotto il segno di integrale scriviamo
∂L∂p = − 1ln 2 ⌠⌡[ln p(x) − p(x)1p(x) + λ1 + λ2x2]dx = 0
in cui si è applicata la regola della derivata del prodotto
p ln p. L’uguaglianza con zero si verifica se
ln p(x) − 1 + λ1 + λ2x2 = 0 ovvero
ln p(x) = 1 − λ1 − λ2x2, da cui
p(x) = e1 − λ1 − λ2x2 = e1 − λ1 e− λ2x2 = eαe− βx2
dove
α = 1 − λ1 e
β = λ2 deve essere positivo per poter avere
∫ p(x) dx finito.
Osserviamo ora che il vincolo
∫ p(x) dx = 1 determina che
∫ eα e− βx2 dx = eα√π⁄β = 1 e dunque la condizione
g1(p) = 0 è soddisfatta qualora
eα = √β⁄π
Infine, il vincolo
∫ x2p(x) dx = σ2 impone che
⌠⌡ x2 eαe− βx2 dx = √β⁄π ⌠⌡ x2 e− βx2dx = σ2
che risulta soddisfatta qualora
β = 1⁄2σ2, ottenendo infatti in tal modo per
p(x) l’espressione di una gaussiana ovvero
p(x) = eαe− βx2 = √β⁄πe− βx2|β = 1⁄2σ2 = 1√2πσ2 e− x22σ2
Notiamo esplicitamente la differenza rispetto al caso continuo, in cui la d.d.p. che rende massima l’entropia è invece quella uniforme. Presso
Wikipedia è possibile trovare un elenco di valori di entropia differenziale calcolata per diverse scelte di d.d.p.
9.6.3 Misura di piattezza spettrale di processo gaussiano
Per dimostrare la seconda eguaglianza della
(10.252) occorre prima mettere in evidenza alcune proprietà degli
autovalori λi, i = 1, 2⋯, n della matrice di correlazione
Rxx simmetrica, definita positiva, di dimensioni
n × n, e con valori
Rxx(i, j) = E{xixj} valutati per i campioni
xi di un processo a media nulla, e dunque pari a
σ2x sulla diagonale.
Come noto da altri corsi, ad ogni autovalore
è associato il relativo
autovettore vi dalla relazione
Rxxvi = λivi, e l’insieme degli autovalori può essere trovato risolvendo
l’equazione caratteristica det(Rxx − λI) = 0 dove
I è la matrice
identità, diagonale
n × n. Tale equazione è un polinomio di grado
n in
λ e le peculiarità di
Rxx assicurano di poter trovare
n zeri reali, a partire dai quali possono essere trovati gli autovettori corrispondenti a meno di un fattore di scala, che conviene fissare in modo che gli autovettori siano
ortonormali, ossia per essi valga la relazione
v⊤ivj = δij. Sussistono ora le relazioni
- Rxx = ∑ni = 1λiviv⊤i
- det(Rxx) = ∏ni = 1λi
- tr(Rxx) = ∑ni = 1λi ma dato che è anche vero che tr(Rxx) = nσ2x, per qualunque n il valor medio degli autovalori eguaglia la varianza, ovvero
- σ2x = 1n ∑ni = 1 λi. Essendo quindi gli autovalori una misura di varianza, sono non-negativi. Inoltre, se λi è autovalore di Rxx, allora 1⁄λi è autovalore di R− 1xx.
A questo punto il
colpo di scena deriva dall’applicazione del
teorema di distribuzione di Toeplitz (teorema di Szego) che afferma che per qualunque funzione
f(.)
in cui
Sxx(e jω) = ∑∞k = −∞Rxx(k)e− jkω è la
dtft (§
4.4) della funzione di autocorrelazione
Rxx(k) = E{xnxn + k} cui valori compaiono nella matrice
Rxx,, calcolata per la sequenza
{xn}, di cui
Sxx(e jω) è lo spettro di densità di potenza. In base all’osservazione 4., qualora
f(.) sia pari ad una identità la
(10.260) diviene un aspetto del teorema di Parseval, e calcola la potenza di
{xn}. Ma ora si compie
una magia, poiché ponendo invece
f(.) = ln (.) l’eq.
(10.260) diventa
da cui in base all’osservazione 2 ne consegue
limn → ∞(det(Rxx))1⁄n = exp⎧⎨⎩12ππ⌠⌡ − πln [Sxx(e jω)] dω⎫⎬⎭ = η2x
dove
η2x individua la varianza del
minimo errore di predizione, ossia la varianza del processo bianco in ingresso ad un filtro autoregressivo (vedi §
10.1.2.2) alla cui uscita si ottiene un segnale con autocorrelazione
Rxx(k). Dividendo
η2x per
σ2x = E{x2} = 1 2π ∫ π−π Sxx(e jω) dω otteniamo la
misura di piattezza spettrale
che compare nella
(10.252).
9.6.4 Autocorrelazione di sequenza autoregressiva
Sviluppiamo qui i passaggi necessari ad ottenere le grandezze indicate nell’esempio di pag.
1, osservando innanzitutto che il processo
x(n) = z(n) + α ⋅ x(n − 1) viene anche detto Markoviano di primo ordine, dato che la dipendenza statistica dal passato si estende al solo campione precedente. Come osservato, x(n) è l’uscita di un filtro iir del primo ordine al cui ingresso sono posti campioni di un processo gaussiano bianco a media nulla con varianza σ2z. Per il valore di autocorrelazione, come noto (§
7.4) risulta
Rxx(k) = Rhh(k) * Rzz(k) = σ2z Rhh(k)
in quanto
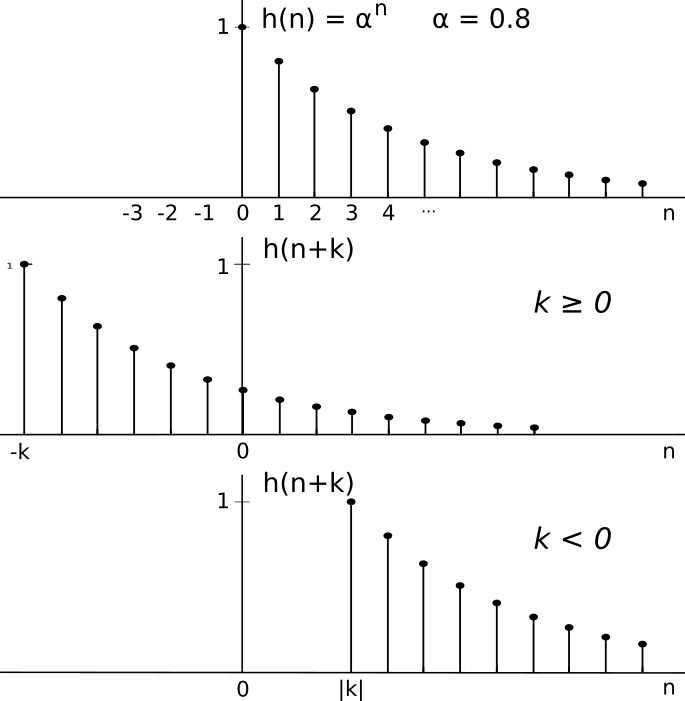
Rzz(k) = σ2zδ(k). Con riferimento alla figura che segue, per
k ≥ 0 si ha
Rhh(k) = ⎲⎳∞n = 0 h(n)h(n + k) = ⎲⎳∞n = 0 αnαn + k = = αk⎲⎳∞n = 0 α2n = αk1 − α2
mentre per
k < 0
Rhh(k) = ⎲⎳∞n = |k| h(n)h(n + k) = ⎲⎳∞n = |k| αnαn + k = = α − k⎲⎳∞n = |k| α2(n + k) = α − k⎲⎳∞n = 0 α2n = α − k1 − α2
ma dato che se
k < 0 allora
− k = |k|, possiamo scrivere
Rhh(k) = α|k| 1 − α2
per
∀k. Risulta quindi
Rxx(k) = σ2z Rhh(k) = σ2z α|k| 1 − α2
a cui corrisponde una varianza
σ2x = Rxx(0) = σ2z 11 − α2
ottenendo in definitiva
Rxx(k) = σ2zα|k|
Applicando poi la definizione
(10.262) di piattezza spettrale otteniamo
γ2x = σ2zσ2x = σ2z 1 − α2 σ2z = 1 − α2
mentre la risposta in frequenza
Hxx(e jω) è stata già ricavata a pag.
1, eq.
(10.82).