Distribuzione di Poisson

Prec Sezione 17.1: Distribuzione binomiale per popolazione finita Su Capitolo 17: Sistema di servizio, teoria del trafficoe delle reti Sezione 17.3: Sistema di servizio orientato alla perdita Segue

17.2 Distribuzione di Poisson

Al crescere del numero N di utenti, l’utilizzo della distribuzione Binomiale può risultare disagevole, per via dei fattoriali, e si preferisce trattare il numero di conversazioni attive k come una variabile aleatoria di poisson↓, la cui densità di probabilità ha espressione

(19.2) p_P(k) = e^− α(α^k)/(k!)

ed è caratterizzata da valor medio e varianza m_p = σ²_P = α. La Poissoniana costituisce una buona

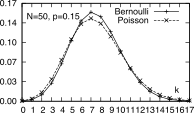approssimazione della ddp di Bernoulli, adottando per la prima lo stesso valor medio della seconda m_P = m_B, ossia α = Np, come mostrato in figura.

Più in generale, questa densità è impiegata per descrivere la probabilità che si verifichino un numero di eventi indipendenti e completamente casuali↓ di cui è noto solo il numero medio α( [841] [841] Usando il modello Poissoniano pertanto, la probabilità che (ad esempio) si stiano svolgendo meno di 4 conversazioni contemporanee è pari a p_P(0) + p_P(1) + p_P(2) + p_P(3) = e^− α⎛⎝1 + α + (α²)/(2) + (α³)/(6)⎞⎠.). D’altra parte, al tendere di N ad ∞ il modello Bernoulliano adottato finora perde di validità. Infatti, nel caso di una popolazione infinita, il numero di nuove chiamate non diminuisce all’aumentare del numero dei collegamenti in corso. In questo caso, gli eventi corrispondenti all’inizio di una nuova chiamata sono invece considerati indipendenti e completamente casuali, e descritti unicamente in base ad una frequenza media di interarrivo↓ λ che rappresenta la velocità [842] [842] λ viene espresso in richieste per unità di tempo. con cui si presentano le nuove chiamate [843] [843] La trattazione può facilmente applicarsi a svariate circostanze: dalla frequenza con cui si presentano richieste di collegamento ad una rete di comunicazioni, alla frequenza con cui transitano automobili sotto un cavalcavia, alla frequenza con cui particelle subatomiche transitano in un determinato volume, alla frequenza con cui gli studenti si presentano a lezione.... L’inverso di λ rappresenta un tempo,

Tempi di Interarrivo

ed esattamente τ_a = 1 ⁄ λ è il valor medio della variabile aleatoria τ_a costituita dall’intervallo di tempo tra l’arrivo di due chiamate.

Con queste definizioni, è possibile riferire la v.a. di Poisson ad un intervallo temporale di osservazione T, durante il quale si presentano un numero medio α di chiamate [844] [844] Esempio: se da un cavalcavia osserviamo (mediamente) λ = 3 auto/minuto, nell’arco di T = 2 minuti, transiteranno (in media) 3*2 = 6 autovetture. pari a α = λT. Pertanto, possiamo scrivere la ddp della v.a. Poissoniana come

p_P(k)|_T = e^− λT((λT)^k)/(k!)

che indica la probabilità che in un tempo T si verifichino k eventi (indipendenti e completamente casuali) la cui frequenza media è λ( [845] [845] Esempio: sapendo che l’autobus (completamente casuale!) che stiamo aspettando ha una frequenza di passaggio (media) di 8 minuti, calcolare: A) la probabilità di non vederne nessuno per 15 minuti e B) la probabilità che ne passino 2 in 10 minuti.

Soluzione: si ha λ = 1 ⁄ 8 passaggi/minuto e quindi: A) p_P(0)|₁₅ = e^{− (15)/(8)} = 0.15 pari al 15%; B) p_P(2)|₁₀ = e^{− (10)/(8)}(⎛⎝(10)/(8)⎞⎠²)/(2) = 0.224 pari al 22.4%

17.2.1 Variabile aleatoria esponenziale negativa↓

La descrizione statistica che la ddp di Poisson fornisce per il numero di eventi che si verificano in un (generico) tempo t, è strettamente legata al considerare questi come indipendenti, identicamente distribuiti, e per i quali l’intervallo di tempo tra l’occorrenza degli stessi è una determinazione di variabile aleatoria completamente casuale [846] [846] Da un punto di vista formale, per eventi completamente casuali si intende che gli eventi stessi non hanno memoria di quando siano accaduti l’ultima volta, permettendo quindi di scrivere

Pr(t > t₀ + θ ⁄ t > t₀) = Pr(t > θ)

ossia che la probabilità di attendere altri θ istanti, avendone già attesi t₀, non dipende da t₀. Per verificare che la ddp esponenziale consente di soddisfare questa condizione, svolgiamo i passaggi, applicando al terzultimo la (19.3↓):

Pr(t > t₀ + θ ⁄ t > t₀) = (Pr(t > t₀ + θ;t > t₀))/(Pr(t > t₀)) = (Pr(t > t₀ + θ))/(Pr(t > t₀)) = = (e^{− λ(t₀
+ θ)})/(e^− λt₀) = e^− λθ = Pr(t > θ)

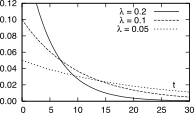
, descritta da una densità di probabilità esponenziale negativa [847] [847] La ddp esponenziale è spesso adottata come un modello approssimato ma di facile applicazione per rappresentare un tempo di attesa, ed applicato ad esempio alla durata di una conversazione telefonica, oppure all’intervallo tra due malfunzionamenti di un apparato., espressa analiticamente come

p_E(t) = λe^− λt

valida per t ≥ 0, e mostrata in figura; tale v.a. è caratterizzata dai momenti [848] [848] Per quanto riguarda il valor medio m_E = ∫^∞₀tλe^− λtdt possiamo procedere per parti, ossia applicando la regola ∫^b_af’(t)g(t)dt = f(t)g(t)|^b_a − ∫^b_af(t)g’(t)dt, avendo posto f’(t) = e^− λt e g(t) = λt: si ottiene allora

m_E = − (1)/(λ)e^− λt⋅λt||^∞₀ − ^∞⌠⌡₀ − (1)/(λ)e^− λt⋅λdt = − 0 + 0 − (1)/(λ)e^− λt||^∞₀ = (1)/(λ)

essendo lim_{t → ∞}e^− λt⋅λt = 0. Per σ²_E = ∫^∞₀t²λe^− λtdt − (m_E)², il primo integrale (sempre procedendo per parti) fornisce ∫^∞₀t²λe^− λtdt = (2)/(λ²), e dunque σ²_E = (2)/(λ²) − (1)/(λ²) = (1)/(λ²). m_E = (1)/(λ) e

Variabile aleatoria esponenziale negativa

Densità di v.a. Esponenziale

σ²_E = (1)/(λ²). La probabilità che il tempo di attesa di una v.a. esponenziale superi un determinato valore t₀, è allora calcolabile come

(19.3) Pr(t > t₀) = ^∞⌠⌡_t₀λe^− λtdt = − e^− λt|^∞_t₀ = e^− λt₀

e questo risultato ci permette di verificare il legame con la Poissoniana [849] [849] Consideriamo un ospedale in cui nascono in media 6 bimbetti al giorno (o 0.25 nascite l’ora), e consideriamo l’intervallo tra questi eventi come una v.a. completamente casuale. Se assumiamo che la probabilità di k nascite in un tempo T sia descritta da una v.a. di Poisson, ossia a cui compete una probabilità p_P(k) = e^− λT((λT)^k)/(k!), allora la probabilità che durante un tempo T non avvenga nessuna nascita, dovrebbe corrispondere a calcolare p_P(0), ovvero e^− λT((λT)⁰)/(0!) = e^− λT, che è esattamente il risultato che fornisce la v.a. esponenziale per la probabilità Pr(t > T) che non vi siano nascite per un tempo T..

Esempio Se la durata media di una telefonata è di 5 minuti, e la durata complessiva è completamente casuale, quale è la probabilità che la stessa duri più di 20 minuti?

Risposta: ci viene fornito un tempo di attesa medio τ_a, a cui corrisponde una frequenza di servizio λ = (1)/(τ_a), e quindi la soluzione risulta Pr(t > 20) = ∫^∞₂₀(1)/(τ_a)e^{− t ⁄ τ_a}dt = e^{− 20 ⁄ 5} = 0.0183 = 1.83%.

Un corollario [850] [850] La dimostrazione della (19.4↓) si basa sulla considerazione che Pr(t ≤ t₀) = 1 − Pr(t > t₀), e sulla espansione in serie di potenze e^x = 1 + x + ^x²⁄₂ + ^x³⁄_3! + ⋯ che si riduce a e^x = 1 + x + o(t₀) se x → 0. Pertanto, la (19.3↑) diviene Pr(t > t₀)|_{t₀
→ 0} = 1 − λt₀ + o(t₀), e quindi Pr(t ≤ t₀) = 1 − 1 + λt₀ + o(t₀) = λt₀ + o(t₀). della (19.3↑) è che, se t₀ → 0, allora la probabilità che si verifichi un evento entro un tempo t₀, è direttamente proporzionale (a meno di un infinitesimo di ordine superiore di t₀) al valore di t₀, ossia

(19.4) Pr(t ≤ t₀)|_{t₀
→ 0} = λt₀ + o(t₀)

Prec Sezione 17.1: Distribuzione binomiale per popolazione finita Su Capitolo 17: Sistema di servizio, teoria del trafficoe delle reti Sezione 17.3: Sistema di servizio orientato alla perdita Segue