Prec Sezione 6.7: Filtri digitali
Su
Capitolo 6: Densità spettrale e filtraggio Sezione
6.9: Appendici Segue
6.8 Filtri analogici↓
Sono
ottenuti mediante componenti elettrici a costanti concentrate come
condensatori, induttori e resistori. Applicando la trasformata di Laplace
alle equazioni differenziali che descrivono la relazione
ingresso-uscita, si ottiene una funzione di trasferimento↓
razionale del tipo
H(s) = (N⎲⎳i
= 0aisi)/(M⎲⎳j = 0bjsj)
(in cui N ≤ M), definita su
di un piano complesso s = σ + j2πf.
Ponendo s = j2πf
si ottiene la funzione di trasferimento in f:
H(f) = H(s
= j2πf).
Questo procedimento è valido solo se il filtro è stabile, che nel
dominio di Laplace equivale a richiedere che tutti i poli di H(s)
siano a sinistra dell’asse immaginario. 6.8.1 Filtro analogico ad un polo
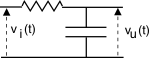
h(t) = (1)/(RC)e
− (t)/(RC)
L’analisi del circuito mostra che la funzione di
trasferimento risulta
H(f) = ℱ{h(t)} = (1 ⁄ jωC)/(R + 1 ⁄ jωC) = (1)/(1 + j2πfRC)
ovvero, nel dominio di Laplace
H(s) = (1)/(1 + sRC)
Pertanto, H(s) presenta un polo in s
= − (1)/(RC) che fa sì che H(s)|s
= − (1)/(RC) = ∞. 
6.8.2 Frequenza di taglio ↓

|H(fT)| = (|HMax|)/(√(2))
Nel caso del filtro RC, si ha |HMax| = H(0) = 1 e dunque scriviamo
|H(f)| = (1)/(√(1 + (2πfRC)2)) = (1)/(√(1 + ⎛⎝(f)/(fT)⎞⎠2))
in cui fT = (1)/(2πRC),
pari quindi alla frequenza di taglio (infatti |H(fT)| = (1)/(√(1 + 1))
= (1)/(√(2))). Notiamo infine che |H(fT)|2 =
(1)/(2) e dunque |H(fT)|2|dB
= -3 dB; per questo la frequenza di taglio è indicata anche
come frequenza a 3 dB. 6.8.3 Assenza di distorsione lineare↓
Quali proprietà devono essere verificate da un
filtro affinché l’uscita non differisca dall’ingresso per più di un
fattore di scala ed un ritardo, ovvero si verifichi la proprietà di canale
perfetto espressa a pag. 1↓?
La condizione cercata si esprime come
 y(t) = αx(t
− t0), che
corrisponde a Y(f) = αX(f)e − j2πft0,
e quindi la risposta in frequenza di tale filtro deve essere del tipo
y(t) = αx(t
− t0), che
corrisponde a Y(f) = αX(f)e − j2πft0,
e quindi la risposta in frequenza di tale filtro deve essere del tipo

H(f) = (Y(f))/(X(f))
= αe − j2πft0
ovvero la sua risposta impulsiva è pari a h(t) = αδ(t − t0).
Pertanto le condizioni poste nel tempo, si riflettono su di una risposta
in frequenza con modulo costante e fase lineare,
quantomeno, nella banda del segnale. Prec Sezione 6.7: Filtri digitali
Su
Capitolo 6: Densità spettrale e filtraggio Sezione
6.9: Appendici Segue
 Nato più di 20 anni fa, un progetto di
Nato più di 20 anni fa, un progetto di