22.3 Sistema di servizio orientato alla perdita
Un
sistema di servizio è una entità in grado di accogliere delle
richieste di servizio, ovvero eventi che definiscono il cosiddetto
processo di ingresso al sistema, fino al raggiungimento della capacità limite, determinata dal numero
M di
serventi di cui il
sistema dispone. Una volta occupati tutti i serventi, e finché non se ne libera qualcuno, le successive richieste possono essere poste in coda, individuando così un sistema
orientato al ritardo (che affrontiamo al §
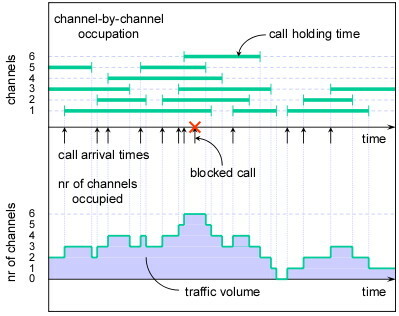
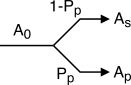
22.4), oppure rifiutate (vedi la figura a fianco), come avviene per i sistemi
orientati alla perdita. Scopo della presente sezione è quindi quello di determinare il numero di serventi necessario a garantire una
probabilità di rifiuto della richiesta di servizio pari ad un valore che descrive il
grado di servizio che si intende fornire.
22.3.1 Frequenza di arrivo e di servizio
Mentre il processo di ingresso è descritto in termini della
frequenza media di arrivo
λ, il tempo medio di occupazione dei serventi (indicato come
processo di servizio) è descritto nei termini del
tempo medio di servizio τS, ovvero dal suo inverso
μ = 1 ⁄ τS, pari alla
frequenza media di servizio
. Nella trattazione seguente si fa l’ipotesi che entrambi i processi (di ingresso e di servizio) siano descrivibili in termini di v.a. a distribuzione esponenziale, ovvero che le durate degli eventi “nuova richiesta” e “servente occupato” siano
completamente casuali.
22.3.2 Intensità media di traffico
Il rapporto Ao = λμ è indicato come intensità media del traffico offerto e descrive quanti serventi (in media) sarebbero occupati ad espletare le richieste arrivate e non ancora servite, nel caso in cui M fosse infinito. L’aggettivo offerto indica la circostanza che, essendo invece M finito, alcune richieste non sono accolte, ed Ao risulta diverso dal traffico As che può essere effettivamente smaltito. L’unità di misura dell’intensità di traffico è l’erlang, il cui valore indica appunto il numero medio di serventi occupati.
Esempio Ad un centralino giungono una media di λ = 3 chiamate al minuto, e la durata media di una conversazione è 1 ⁄ μ = 3 minuti. In tal caso l’intensità media di traffico risulta Ao = 3 ⋅ 3 = 9 Erlang, corrispondenti al potenziale impegno di una media di 9 centralinisti (e nove linee telefoniche).
22.3.3 Probabilità di rifiuto
La teoria che porta a determinare la probabilità che una nuova richiesta di servizio non possa essere accolta a causa dell’esaurimento dei serventi si basa sulla descrizione di un cosiddetto
processo di nascita e morte, che rappresenta da un punto di vista statistico l’evoluzione di una popolazione, nei termini di una frequenza di nascita (nuova conversazione) e di morte (termine della conversazione). Istante per istante, il numero esatto di individui della popolazione può variare, ma in un istante a caso, possiamo pensare alla numerosità della popolazione come ad una variabile aleatoria discreta, descritta in base ai valori di probabilità
pk che la popolazione assommi esattamente a
k individui. La determinazione di questi valori
pk dipende dalla caratterizzazione dei processi di ingresso e di servizio, e nel caso in cui questi siano descritti da v.a. esponenziali (o poissoniane, a seconda se ci riferiamo ai tempi medi di interarrivo/partenza, od al loro numero medio per unità di tempo) si può procedere nel modo che segue.
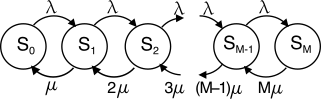
Descriviamo innanzitutto l’evoluzione dello stato del sistema, in cui il numero di
serventi occupati evolve aumentando o diminuendo di una unità alla volta (come per i processi di nascita e morte), con l’ausilio della figura, dove il generico stato
Sk rappresenta la circostanza che
k serventi siano occupati, circostanza a cui compete una probabilità
pk = Pr(Sk).
Gli stati del grafo sono collegati da archi etichettati con la frequenza
λ delle transizioni tra gli stati, ovvero dal ritmo con cui si passa da
Sk a
Sk + 1 a causa di una nuova richiesta, indipendente (per ipotesi) dal numero di serventi già occupati, e dal ritmo
(k + 1) ⋅ μ con cui si torna da
Sk + 1 ad
Sk, a causa del termine del servizio espletato da uno tra i
k + 1 serventi occupati, e proporzionale quindi a questo numero. Se
λ e
μ non variano nel tempo, una volta esaurito un transitorio iniziale il sistema di servizio si troverà in
condizioni stazionarie, permettendoci di scrivere le
equazioni di equilibrio statistico
che eguagliano la frequenza media con cui il sistema evolve dallo stato
k verso
k + 1, alla frequenza media con cui avviene la transizione inversa. La (
26.5) può essere riscritta come
pk + 1 = λμ(k + 1) pk = Ao(k + 1) pk
che applicata ricorsivamente, porta a scrivere
Non resta ora che trovare il modo per dare un valore a
p0, e questo è oltremodo semplice, ricordando che deve risultare
1 = ∑Mm = 0 pm = p0 ∑Mm = 0 Amom!, e quindi
Nei due casi distinti in cui i serventi siano in numero finito (e pari ad
M) od infinito (
M = ∞) otteniamo rispettivamente il caso cercato, ed un caso limite. Se poniamo
M = ∞, tenendo conto dell’espansione in serie
∑∞m = 0 Amom! = eA0, si ottiene che la (
26.7) fornisce appunto
p0 = e − A0, e la (
26.6) diviene
pk = e − A0 Akok!, che come riconosciamo immediatamente è proprio la ddp di Poisson (
26.2) con valore medio
A0. Se invece poniamo
M finito, la sommatoria che compare in (
26.7) non corrisponde ad una serie nota, e dunque rimane come è, fornendo il risultato
pk = Pr(Sk) = Akok!M⎲⎳m = 0 Amom!
Notiamo ora che
pM è la probabilità che tutti i serventi siano occupati, pari dunque alla probabilità che una nuova richiesta di servizio sia rifiutata. Chiamiamo allora questo valore
probabilità di Blocco,
di Rifiuto o
di Perdita, la cui espressione prende il nome di
Formula B di Erlang, del primo tipo, di ordine M ed argomento
Ao:
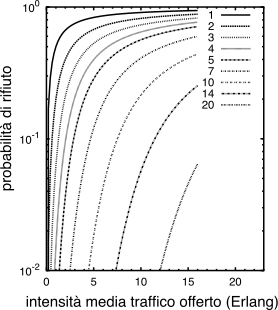
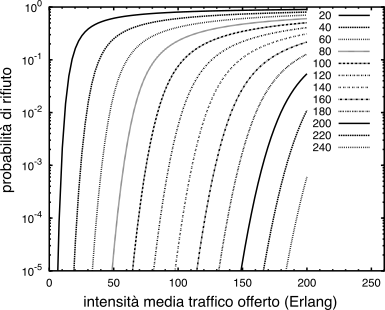
L’andamento di
PB in funzione di
M e di
Ao è graficato in Fig.
22.8, e mostra come (ad esempio) per una intensità di traffico offerto pari a 40 Erlang, siano necessari più di 50 serventi per mantenere una
PB minore dell’1%, che salgono a più di 60 per una
PB = 10 − 3.
22.3.4 Efficienza di giunzione
In presenza di una intensità media di traffico offerto
Ao, ed una probabilità di perdita
Pp = PB, solamente il
(1 − Pp) ⋅ 100 % delle richieste è smaltito, e quindi
Ao si ripartisce tra l’intensità media di
traffico smaltito As = Ao(1 − Pp), e l’intensità media di
traffico perso Ap = AoPp. Possiamo definire un coefficiente di utilizzazione, o efficienza
ρ = AsM = AoM (1 − Pp)
che rappresenta la percentuale di impegno dei serventi,
e di cui la figura
22.10 mostra l’andamento al variare di
Ao, per una
PB assegnata e pari a
2 ⋅ 10 − 3, assieme al numero di serventi necessario a garantire tale probabilità di blocco.
Come si può osservare, una volta fissato il grado di servizio, all’aumentare del numero di serventi il traffico smaltito cresce più in fretta di quanto non crescano i serventi, cosicché (a parità di Pp) l’efficienza aumenta con l’intensità di traffico offerto, e per questo i collegamenti (giunzioni) in grado di smaltire un numero più elevato di connessioni, garantiscono anche una maggiore economicità di esercizio.
22.3.5 Validità del modello
Le considerazioni esposte si riferiscono ad una ipotesi di traffico completamente casuale con tempi di interarrivo e di servizio esponenziali, ossia con un processo di traffico incidente di Poisson. In queste ipotesi, il rapporto σ2PmP = 1 tra la varianza e la media delle distribuzioni di Poisson, è rappresentativo appunto di un traffico completamente casuale.
Del tutto diversa può risultare l’analisi nel caso di una giunzione usata solo nel caso di trabocco del traffico da una giunzione piena. In questo caso
λ non è più costante, anzi aumenta con l’aumentare delle connessioni già avvenute, tipico di
traffico a valanga.
Esempio Un numero molto elevato di sorgenti analogiche condivide uno stesso mezzo trasmissivo, caratterizzato da una capacità complessiva netta di 25.6 Mbps. Le sorgenti sono campionate a frequenza fc = 21.33 KHz e con una risoluzione di 12 bit/campione; ogni sorgente trasmette ad istanti casuali per un tempo casuale, quindi gli intervalli di interarrivo e di servizio sono entrambi v.a. a distribuzione esponenziale negativa, di valor medio rispettivamente λ = 20 richieste/minuto e 1μ = 4.25 minuti.
-
- Determinare la fb di una sorgente nelle fasi di attività;
- determinare il numero massimo di sorgenti contemporaneamente attive;
- determinare il grado di servizio (Probabilità di rifiuto) ottenibile con il mezzo trasmissivo indicato;
- indicare la capacità da aggiungere al collegamento per garantire un grado di servizio cento volte migliore.
Risposte
-
-
fb = bitcampione ⋅ campionisecondo = 12 ⋅ 21.33 ⋅ 103 = 256
Kbps;
- Il numero massimo di sorgenti contemporaneamente attive coincide con il numero di serventi M del collegamento, e quindi M = 25.6 ⋅ 106256 ⋅ 103 = 100 serventi;
- L’intensità media di traffico offerto risulta pari a Ao = λμ = 201 ⁄ 4.25 = 85 Erlang, e pertanto dalle curve di Fig. 22.8 si trova una probabilità di rifiuto pari a circa 10 − 2:
- Si richiede quindi una probabilità di rifiuto 100 volte inferiore, e cioè pari a 10 − 4: si ottiene che la banda deve essere aumentata del 20%. Infatti, dalle curve di Fig. 22.8 si osserva che ciò richiede (a parità di Ao) almeno 120 (circa) serventi, 20 in più, pari ad una capacità aggiuntiva di 20 ⋅ 256 ⋅103 = 5.12 Mbps.