Sezione 22.3: Sistema di servizio orientato alla perdita Su Capitolo 22: Sistema di servizio, teoria del traffico, e delle reti Sezione 22.5: Reti per trasmissione dati 

22.4 Sistemi di servizio orientati al ritardo

Mentre i sistemi orientati alla perdita rappresentano il modo di operare delle reti di telecomunicazione a commutazione di circuito, in cui ogni connessione impegna in modo esclusivo alcune risorse di rete, che una volta esaurite producono un rifiuto della richiesta di connessione, i sistemi orientati al ritardo sono rappresentativi di reti a commutazione di pacchetto, in cui i messaggi sono suddivisi in unità elementari (detti pacchetti, appunto) la cui ricezione non deve più avvenire in tempo reale, e che condividono le stesse risorse fisiche (degli organi di commutazione e di trasmissione) con i pacchetti di altre comunicazioni. Pertanto, l’invio di un pacchetto può essere ritardato se il sistema di servizio è in grado di gestire delle code di attesa, in cui accumulare le richieste che eccedono il numero di serventi a disposizione, e da cui prelevare (con ritardo) i pacchetti stessi non appena si rendano disponibili le risorse trasmissive necessarie.
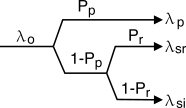
figure f6.10.png
In questo caso lo schema che esemplifica la ripartizione dei flussi di richieste si modifica come in figura, dove è evidenziato come la frequenza di richieste λo si suddivide tra la frequenza delle richieste perse λp, quelle servite con ritardo λsr, e quelle servite immediatamente λsi, in funzione della probabilità di perdita Pp e di ritardo Pr. Nei termini di queste quantità, valgono le relazioni:
λp = Ppλo;     λsr = Pr(1 − Pp)λo;     λsi = (1 − Pr)(1 − Pp)λo
Indicando con τS = 1μ il tempo medio di servizio di ogni richiesta, (che non comprende quindi il tempo di accodamento), si definisce, come già noto, una intensità di traffico offerto Ao = λoμ = λoτS, che deve risultare
Ao = Ap + Asr + Asi       e  quindi      Asr = λsrμ,    Asi = λsiμ
Considerando il caso in cui la coda abbia una lunghezza finita e pari ad L, osserviamo che, a prima vista, anche le L richieste successive all’impegno di tutti gli M serventi sono accolte (e poste in coda), come se i serventi fossero divenuti M + L. In realtà l’analisi fornisce risultati differenti, in quanto le richieste accodate devono essere ancora servite, e quindi il calcolo della Pp non è una diretta estensione dei risultati ottenuti per i sistemi orientati alla perdita. E’ comunque abbastanza semplice verificare [1328]   [1328] Se PB è la probabilità di blocco derivante dalla disponibilità di M serventi, una frequenza di richieste pari a PB ⋅ λo non può essere servita immediatamente; adottando una coda, la frequenza delle richieste non servite immediatamente PB ⋅ λo è uguale a λo(Pp + Pr(1 − Pp)), ed eguagliando le due espressioni si ottiene Pp = PB − Pr1 − Pr, che è sempre minore di PB. che ora la Pp risulta inferiore alla PB del caso senza coda, e pertanto l’intensità di traffico smaltito As = Asr + Asi = (1 − Pp)Ao aumenta, a parità di offerta.

22.4.1 Risultato di Little

Si tratta di un risultato molto generale, valido per qualsiasi distribuzione dei tempi di interarrivo e di servizio, la cui applicazione può tornare utile nell’analisi, e che recita:
Il numero medio N di utenti contemporaneamente presenti in un sistema di servizio è pari al prodotto tra frequenza media di smaltimento delle richieste λs ed il tempo medio di permanenza τp dell’utente nel sistema
e quindi in definitiva N = λs ⋅ τp. Nell’applicazione al caso di servizi orientati alla perdita, si ha τp = τS, mentre nei servizi a coda risulta τp = τc + τS in cui τc rappresenta il tempo medio di coda.

22.4.2 Sistemi a coda infinita ed a servente unico

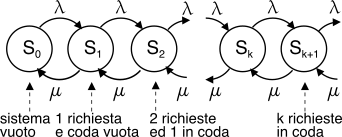
Prima di fornire risultati più generali, svolgiamo l’analisi per questo caso particolare, in cui la frequenza di richieste perse λp è nulla, dato che una coda di lunghezza infinita le accoglie comunque tutte. Da un punto di vista statistico un tale sistema è descritto mediante il
figure f6.11.png
diagramma di nascita e morte riportato a fianco, in cui ogni stato Sk rappresenta k richieste nel sistema, di cui una sta ricevendo servizio e k − 1 sono accodate.
Per procedere nell’analisi si applica lo stesso principio di equilibrio statistico già adottato a pag. 1 dove si asserisce che, esaurito un periodo transitorio iniziale, la frequenza media delle transizioni tra Sk e Sk + 1 deve eguagliare quella da Sk + 1 ad Sk. Indicando con pk = Pr(Sk) la probabilità che il sistema contenga k richieste, l’equilibrio statistico si traduce nell’insieme di equazioni
(26.9)
λo pk = μ pk + 1      con  k = 0, 1, 2, …, ∞
Infatti, in base alle stesse considerazioni svolte nella prima parte della nota 1322 di pag. 1, λopk è pari alla frequenza media (frazione di λo) con cui il numero di richieste accolte passa da k a k + 1; essendo il servente unico, la frequenza di servizio è sempre μ = 1τS,  indipendentemente dal numero di richieste accodate, e dunque μpk + 1 è proprio la frequenza media con cui il sistema passa da k + 1 a k richieste accolte.
La relazione (26.9) è di natura ricorsiva, e può esprimersi come
pk = ⎛⎝λoμ⎞⎠k p0 = Ako p0
Per determinare il valore p0 = Pr(S0), uguale alla probabilità che il sistema sia vuoto, ricordiamo [1329]   [1329] Nella derivazione del risultato si fa uso della relazione ∑∞k = 0αk = 11 − α, nota con il nome di serie geometrica, e valida se α < 1, come infatti risulta nel nostro caso, in quanto necessariamente deve risultare Ao = λoμ < 1; infatti se il servente è unico una frequenza di arrivo maggiore di quella di servizio preclude ogni speranza di funzionamento, dato che evidentemente il sistema non ha modo di smaltire in tempo le richieste che si presentano. che deve risultare
1 = ∞⎲⎳k = 0pk = ∞⎲⎳k = 0p0 Ako = p0 11 − Ao
da cui otteniamo p0 = 1 − Ao e dunque
pk = (1 − Ao) Ako
che corrisponde ad una densità di probabilità esponenziale discreta.
Siamo ora in grado di determinare alcune grandezze di interesse:
Probabilità di ritardo Pr: risulta pari alla probabilità che il sistema non sia vuoto, e cioè che ci sia già almeno una richiesta accolta, ed è pari a [1330]   [1330] Ricordiamo che p0 è la probabilità che il sistema sia vuoto, e dunque 1 − p0 quella che non sia vuoto.
Pr = 1 − po = 1 − (1 − Ao) = Ao
Ricordiamo di aver già definito l’efficienza come il rapporto ρ = AsM tra il traffico smaltito ed il numero dei serventi; nel nostro caso M = 1 e As = Ao: dunque ρ = Ao. Pertanto, il risultato Pr = Ao = ρ indica come, al tendere ad 1 dell’efficienza, la probabilità di ritardo tenda anch’essa ad 1.
Lunghezza media di coda indicata con L: risulta essere semplicemente il valore atteso del numero di richieste presenti nel sistema, ovvero [1331]   [1331]  si fa uso della relazione ∑∞k = 0kαk = α∑∞k = 0kαk− 1 =  α∂∂α ∑∞k = 0αk = α∂∂α 11 − α = α(1 − α)2
L = E{k} = ∞⎲⎳k = 0kpk = (1 − Ao)∞⎲⎳k = 0kAko = Ao1 − Ao
da cui risulta che per Ao → 1 la coda tende ad una lunghezza infinita.
Tempo medio di permanenza indicato con τp, e scomponibile nella somma τp = τS + τc tra il tempo medio di servizio ed il tempo medio di coda. Possiamo applicare qui il risultato di Little N = λs ⋅ τp, che esprime la relazione tra numero medio N di richieste presenti, frequenza di smaltimento (qui pari a quella di offerta [1332]   [1332] Non può essere λs > λo, perché si servirebbero più richieste di quante se ne presentano. Se fosse invece λs < λo, la coda crescerebbe inesorabilmente e sarebbe quindi inutile.), e tempo medio di permanenza; infatti accade che N = L, ed utilizzando il risultato L = Ao1 − Ao si ottiene
τp = Nλs = Lλo = Ao1 − Ao 1λo = λoμ 1λo 11 − λo ⁄ μ = 1μ − λo
da cui si osserva che, se la frequenza di offerta tende al valore della frequenza di servizio, il tempo medio di permanenza tende ad ∞.
Tempo medio di coda si calcola come
τc = τp − τS = 1μ − λo − 1μ = μ − μ + λoμ(μ − λo) = Aoμ(1 − Ao) = 1μ ρ1 − ρ = τS ρ1 − ρ
Questo risultato mostra che il tempo medio di coda è legato al tempo medio di servizio e all’efficienza di giunzione, confermando ancora i risultati per ρ → ∞.
La fig. 22.13 mostra l’andamento delle grandezze appena calcolate.
figure f6.77a.png figure f6.77b.png
figure f6.77c.png figure f6.77d.png
Figure 22.13 Grandezze di interesse per il sistema a coda infinita ed unico servente

22.4.3 Sistemi a coda finita e con più serventi

Riportiamo solo i risultati, validi se entrambi i processi di ingresso e di servizio sono esponenziali con frequenza media λo e μ, la coda è lunga L, i serventi sono M e le sorgenti infinite.
Probabilità di k richieste nel sistema 
pk(Ao) = ⎧⎪⎪⎨⎪⎪⎩ Akok!α(Ao) 0 ≤ k ≤ M AkoMk − MM!α(Ao)     M ≤ k ≤ M + L
in cui α(Ao) = 1p0(Ao) = ∑M + Lk = 0Akok!  e Ao = λoμ. Si noti come per 0 ≤ k ≤ M ed L = 0 si ottenga lo stesso risultato già esposto per i sistemi orientati alla perdita, mentre per M = 1 ed L = ∞ ci si riconduca al caso precedentemente analizzato.
Probabilità di ritardo 
Pr = M + L⎲⎳k = Mpk(Ao) = pM(Ao) 1 − ρL + 11 − ρ      in cui  ρ = AoM
Probabilità di perdita 
Pp = pM + L(Ao) = AM + LoMLM! ⋅ α(Ao)
Tempo medio di coda 
τc = τSPr − L ⋅ PM + L(Ao)M − Ao
La Figura 22.14 descrive la probabilità di perdita per un sistema a servente singolo (a sinistra) e con 10 serventi (a destra), in funzione dell’intensità di traffico offerto e della lunghezza di coda L, così come risulta dalla applicazione delle formule riportate.
figure f6.115.png
figure f6.116.png
Figure 22.14 Probabilità di perdita per un sistema a coda finita con uno o dieci serventi
Nel caso di trasmissione di pacchetti di lunghezza fissa, per i quali il tempo di servizio è fisso e non a distribuzione esponenziale [1333]   [1333] In una trasmissione a pacchetto, operata a frequenza binaria fb e con pacchetti di lunghezza media Lp bit, il tempo medio di servizio per un singolo pacchetto è pari a quello medio necessario alla sua trasmissione, e cioè τS = Lp ⁄ fb., i risultati ottenuti costituiscono una stima conservativa delle prestazioni del sistema (che potranno cioè essere migliori). L’analisi delle curve permette di valutare con esattezza il vantaggio dell’uso di una coda (a spese del tempo di ritardo). Infatti, aumentando il numero di posizioni di coda si mantiene una probabilità di blocco accettabile anche per traffico intenso.
Ad esempio, per Pb = 1% ed M = 1, osserviamo che una coda con L = 20 posizioni gestisce un traffico di Ao = 0.83 Erlang, contro gli Ao = 0.11 Erlang del caso senza coda. Ciò corrisponde ad un aumento dell’efficienza di 0.830.11 = 7.54 volte. D’altra parte ora il tempo medio di coda (calcolato in modo conservativo applicando la relazione per coda infinita) è τc = τSρ1 − ρ = 0.831 − 0.83τS = 4.9 τS, ed è quindi aumentato (rispetto a τS) di quasi 5 volte.
Esercizio Un nodo di una rete per dati effettua la multiplazione di pacchetti di dimensione media di 8 KByte [1334]   [1334] 1 byte = 8 bit, 1 K = 210 =  1024. Il “K” in questione è “un K informatico”. Nel caso invece in cui ci si riferisca ad una velocità di trasmissione, il prefisso K torna a valere 103 = 1000. su collegamenti con velocità binaria fb = 100 Mbps [1335]   [1335] In virtù di quanto esposto alla nota precedente, in questo caso 1M = 106 = 1000000.
Risposte
 Sezione 22.3: Sistema di servizio orientato alla perdita Su Capitolo 22: Sistema di servizio, teoria del traffico, e delle reti Sezione 22.5: Reti per trasmissione dati