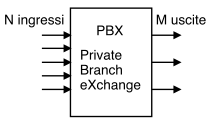
22.1 Distribuzione binomiale per popolazione finita
Iniziamo con il chiederci quante linee uscenti
M siano necessarie ad un centralino
con
N interni, in modo che la probabilità di trovare tutte le linee occupate sia inferiore ad un valore massimo, chiamato
grado di servizio. Per trovare il risultato, calcoliamo prima la probabilità che tutte le linee uscenti siano occupate, assumendo noti
N ed
M.
Affrontiamo il problema in termini ancor più generali, chiedendoci quale sia la probabilità
pB(k) che un numero
k di persone (su
N) sia contemporaneamente al telefono. Assumiamo che ognuno degli
N interni abbia una probabilità
p di telefonare, ossia passi il
p ⋅ 100% del suo tempo al telefono, e che le telefonate siano statisticamente indipendenti. Allora, ci saranno in media
Np telefoni occupati, e la probabilità che un ben preciso gruppo di
k individui telefoni (e
N − k no), è pari a
pkqN − k
in cui
q = 1 − p. Dato che il numero di differenti modi di scegliere
k oggetti tra
N è pari al
coefficiente binomiale
⎛⎜⎝Nk⎞⎟⎠ = N!k!(N − k)! = N(N − 1)⋯(N − k + 1)k!
allora la probabilità di avere
k (qualsiasi) persone al telefono è pari a
Risultando che
∑Nk = 0pB(k) = 1, la funzione
pB(k) rappresenta una densità di probabilità di v.a. discreta, detta anche variabile aleatoria di
Bernoulli o
binomiale.
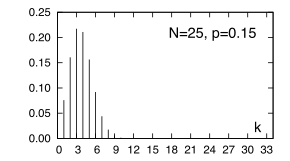
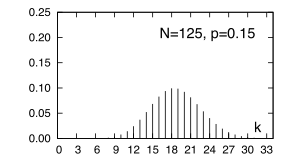
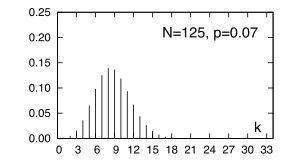
Al variare di k si ottengono tutte le probabilità cercate, rappresentate nella figura a lato nel caso in cui p = 0.15 e N = 25, oppure N = 125. Nel secondo caso, si utilizza anche il valore p = 0.07, che produce una concentrazione di pB(k) attorno a valori k inferiori; valori di p ancora più piccoli producono una d.d.p. che descresce monotonamente per k > 0. Infine, osserviamo che non si possono avere più di N utenti al telefono.
Per conoscere il numero di linee necessarie a garantire una probabilità di
congestione (o di blocco)
PB inferiore ad un massimo, si sommano (partendo
da destra) i valori di probabilità
pB(k), finché non si supera la probabilità prefissata: allora
M sarà pari all’ultimo indice
k. Infatti in tal modo la probabilità che ci siano più di
M interni a voler telefonare è pari a
Pr(k > M) = N⎲⎳k = M + 1pB(k) = N⎲⎳k = M + 1⎛⎜⎝N k⎞⎟⎠ pkqN − k < PB
La distribuzione binomiale è detta anche
delle prove ripetute poiché può essere usata per calcolare la probabilità di un certo numero di eventi favorevoli, a seguito della ripetizione dello stesso fenomeno aleatorio
. Il valor medio della distribuzione Binomiale è
mB = Np, e la varianza
σ2B = Npq. Tornando al caso del centralino, il numero medio di linee occupate è
Np: tale quantità rappresenta
l’intensità di traffico offerto medio, che si misura in
Erlang: ad esempio, un traffico medio di 3 Erlang corrisponde ad osservare in media 3 linee occupate. Il rapporto
σ2BmB = NpqNp = q < 1
è un indice di come la variabile aleatoria
traffico si distribuisce attorno alla media. Il caso di Bernoulli in cui
σ2BmB < 1 è rappresentativo di un traffico
dolce, che deriva dall’ipotesi di popolazione finita, e che si sostanzia nel fatto che all’aumentare delle linee occupate, diminuisce la probabilità di una nuova chiamata, in quanto diminuiscono le persone
non al telefono.
Esercizio Una linea telefonica risulta occupata per l’80 % del tempo, e le telefonate non durano mai più di 5 minuti. Provando a chiamarla con una cadenza fissa di un tentativo ogni 10 minuti, determinare