Le relazioni fin qui discusse permettono di valutare la perdita di informazione causata dai disturbi, ma dipendono sia dalle probabilità in avanti p(y_j ⁄ x_i) che descrivono il comportamento del canale, sia da quelle a priori p(x_i), che invece attengono alle caratteristiche della sorgente. Vogliamo invece definire una grandezza che esprima esclusivamente l’attitudine (o capacità) del canale a trasportare informazione, indipendentemente dalle caratteristiche della sorgente. Questo risultato può essere ottenuto variando le prob. a priori in tutti i modi possibili, fino a trovare il valore che definisce la capacità di canale per simbolo come il massimo valore dell’informazione mutua media, ottenuto in corrispondenza della migliore sorgente possibile. Il pedice _s sta per simbolo, e serve a distinguere il valore ora definito da quello che esprime la massima intensità di trasferimento dell’informazione espressa in bit/secondo, ottenibile una volta nota la frequenza f_s con cui sono trasmessi i simboli, fornendo per la capacità di canale il nuovo valore [927]   [927] Notiamo l’invarianza di (21.95) rispetto al numero di livelli con cui è effettuata la trasmissione: se M bit sono raggruppati per generare simboli ad L = 2^M livelli, come noto f_s si riduce di M volte, mentre C_s aumenta della stessa quantità, dato che ogni simbolo trasporta ora M bit anziché uno. L’importanza di questa quantità risiede nel teorema fondamentale per canali rumorosi [928]   [928] http://it.wikipedia.org/wiki/Secondo_teorema_di_Shannon già anticipato più volte, che asserisce che per ogni canale discreto senza memoria di capacità C

Il teorema non suggerisce come individuare la tecnica di codifica, né fa distinzioni tra codifica di sorgente e di canale, ma indica le prestazioni limite ottenibili mediante la migliore tecnica possibile, in grado di ridurre a piacere la p_e purché R < C, mettendoci al tempo stesso in guardia a non tentare operazioni impossibili. Da questo punto di vista, le prestazioni conseguibili adottando le tecniche di codifica note possono essere valutate confrontandole con quelle ideali predette dal teorema. Inoltre, dato che la capacità di canale è definita come massimo valore di I(X, Y) per la migliore p(x), qualora la statistica dei messaggi prodotti dal codificatore di sorgente differisca da quella ottima per il canale, l’effettiva informazione mutua media risulterà ridotta rispetto al valore della capacità, così come la massima velocità R.

Consideriamo il caso mostrato in figura, ovvero un canale che trasporta senza errori simboli con L = 2^M livelli: in tal caso l’equivocazione H(Y ⁄ X) è nulla, e la (21.89) permette di scrivere I(X, Y) = H(X), che è massima se P(x_i) = ¹⁄_L per tutti gli i, risultando così C_s = H_max(X) = log₂L = M bit/simbolo, e C = f_s ⋅ C_s = f_s ⋅ M bit/secondo.

Esaminiamo l’effetto della presenza di rumore per questo caso particolare, per il quale a pag. 1 abbiamo valutato l’espressione dell’informazione mutua media, data dalla (21.93), e pari a

I(X, Y) = H_b(p_e + α − 2αp_e) − H_b(p_e)

in cui H_b(p_e) dipende solo dalla probabilità di errore, mentre il termine H_b(p_e + α − 2αp_e) dipende anche dalla statistica di sorgente, e risulta massimizzato e pari ad 1 se p_e + α − 2αp_e = 12, come avviene per qualunque p_e se α = 12, ossia per simboli equiprobabili. Pertanto la capacità del bsc risulta pari a

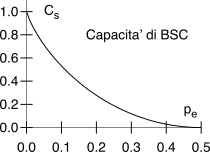
C_s = H_b(¹⁄₂) − H_b(p_e) = 1 − H_b(p_e)

il cui grafico è rappresentato alla figura a lato [931]   [931] Sono mostrati solo i valori per 0 ≤ p_e ≤ 0.5 dato che successivamente l’andamento di C_s si riflette in modo speculare., evidenziando che C_s ≃ 1 bit/simbolo se p_e ≃ 0, ma che poi decade rapidamente a zero se p_e → 0.5.