17.5 Verso il limite di Shannon
I codici a blocco e convoluzionali (e loro combinazioni) esaminati nella precedente sezione sono utilizzati in innumerevoli sistemi anche grazie ai progressi avvenuti nel frattempo dal punto di vista delle capacità di calcolo e memorizzazione, arrivando a conseguire prestazioni che si discostano di circa
3 dB da quelle
limite previste dalla teoria di Shannon (§
17.3.2). Sembrava che non si riuscisse a fare di meglio, quando nei primi anni ’90 sono stati definiti i
turbo-codici (
Berrou, Glavieux), e poco dopo rivalutati i codici
ldpc, inizialmente proposti nel ’62 da
Gallager. Mentre il primo metodo prende le mosse da un nuovo modo di applicare la codifica convoluzionale, il secondo è un codice lineare a blocchi
non sistematico, con
n molto grande (decine di migliaia). In entrambi i casi è determinante l’adozione di una decodifica
soffice, a cui si affianca la novità dell’adozione di un algoritmo
iterativo, in modo da arrivare
per gradi alla decodifica del messaggio. Il risultato è che (sempre grazie all’evoluzione della tecnologia) si è riusciti ad approssimare ancor più da vicino il limite dei
− 1.6 dB per
Eb⁄N0 (§
17.3.4) rispetto al quale mancano solo da
0.7 a
0.5 dB per le due tecniche, determinando la loro adozione da parte dei sistemi più recenti. Vediamo dunque di che si tratta.
17.5.1 Codifica turbo
L’aggettivo turbo deve la sua origine al funzionamento iterativo dell’algoritmo di decodifica, che fa uso dei risultati parziali ottenuti al passo precedente.
La versione di turbo codice più studiata è il
codice convoluzionale concatenato parallelo (
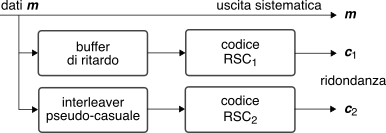
pccc) che consiste nel codificatore
sistematico mostrato in figura, in cui
due
CC ricorrenti (
rsc) uguali elaborano il medesimo bitstream
m di ingresso producendo i bit di protezione
c1 e
c2, tranne che il secondo encoder riceve una copia
rimescolata da parte dell’interleaver, la cui definizione è fondamentale per la riuscita di un turbo codice: grazie ad esso infatti gli ingressi ai due rami divengono istante per istante
incorrelati, così come le rispettive uscite.
La fase di codifica suddivide il bitstream di ingresso
m in segmenti di dimensione
k uguale a quella dell’interleaver, ed applica la tecnica del
tail biting (§
17.4.2.2) in modo da ottenere per ogni ramo una sequenza
c = (c1, ⋯, ck) di
k bit
di protezione del segmento. Alla fine viene quindi trasmessa una parola
x = (m, c1, c2) di
n = 3k bit ottenendo un tasso complessivo
Rc = 1⁄3, eventualmente
aumentato mediante una successiva operazione di perforazione.
Trasmissione e decodifica soft
La figura sotto ha il duplice scopo di riepilogare la
notazione adottata e di evidenziare la presenza di un
canale
soffice che, pur includendo codifica di linea, modem e canale
awgn (§
17.3), non prevede la presenza di un decisore, e dunque fornisce al decodificatore la sequenza
y di valori analogici (
soft) necessaria per la decodifica turbo, con elementi
yj = xj + ε in cui
ε è una v.a. gaussiana a media nulla, varianza
σ2 e valori indipendenti. Il processo di decodifica è anch’esso di tipo soft e per questo detto
siso, ed il suo esito viene espresso come un valore di
verosimiglianza logaritmica a posteriori Lp per ognuno dei
k bit
mi del messaggio informativo, in modo da poter applicare un criterio di massima prob. a posteriori o
map (§
17.1.2) ossia decidere che
m̂j = 1 o
0 a seconda se
Lp(mj) ≷ 0.
Verosimiglianza logaritmica
ed informazione estrinseca
Finché non si attua la decodifica, l’osservazione del valore
yj in uscita dal canale permette il calcolo della verosimiglianza logaritmica a posteriori (nel seguito
llr ossia
log likelihood ratio) per ciascun bit
xj in ingresso al canale soffice come
in cui alla seconda eguaglianza si applica il teorema di Bayes, ed il risultato si interpreta osservando che
L(xj) è somma di due termini: il primo
Lc(yj) è dovuto al canale e dipende solo dal valore
yj ricevuto, mentre il secondo
La(xj) è legato alla prob
a priori di
xj ed è nullo se
0 ed
1 sono equiprobabili.
A differenza della
(21.119), il valore
Lp(xj) = ln Pr(xj = 1 ⁄ y)Pr(xj = 0 ⁄ y) della
llr a posteriori in uscita dal decoder è ottenuto a partire da
tutti i bit ricevuti
y, compresi quelli di ridondanza
c1 e
c2, e per questo la decisione
map presa in base ai valori di
Lp(xj) contiene
meno errori. La variazione della
llr Lp(xj) rispetto alla
(21.119) vale
e prende il nome di
informazione estrinseca in quanto aggiunta da parte del decoder; si può dimostrare che questa
non dipende dai valori di
m, ma solo
da quelli della ridondanza c1 e
c2.
Soft input soft output a quattro porte
L’algoritmo
siso adottato nella decodifica turbo può essere schematizzato come nella figura a fianco, che lo mostra accettare in ingresso le componenti della
llr (21.119) ovvero i contributi delle singole osservazioni
Lc(yj) e quelli a priori
La(xj), e ottenere in uscita sia il valore di
llr a posteriori
Lp(xj) (ottenuta applicando il metodo di decodifica) sia quello della informazione estrinseca ottenuta applicando la
(21.120).
Valutazione della
llr di ingresso e di uscita al
siso
Consideriamo di effettuare una trasmissione binaria antipodale, in cui i valori del segnale agli istanti di simbolo sono espressi come
xj = (2mj − 1) ossia assumono i valori
±1 quando
mi = 1 oppure
0, e lo stesso dicasi per i bit di protezione
c1j e
c2j: in tal caso il termine
Lc(yj) = ln Pr(yj ⁄ xj = 1)Pr(yj ⁄ xj = 0) (eq.
(21.119)) assume il valore
Per quanto riguarda invece
Lp(xi) = ln Pr(xj = 1 ⁄ y)Pr(xj = 0 ⁄ y) diciamo che nel contesto dei codici
rsc usati nel caso in esame il relativo decodificatore opera su di un traliccio analogo a quello visto nella decodifica di Viterbi, ed il valore
Lp(xj) può essere
approssimato ricorrendo ad una decodifica
sova (§
17.4.2.7), ma per ottenere il suo valore esatto (e dunque le migliori prestazioni) occorre ricorrere ad una modifica dell’algoritmo BCJR, le cui problematiche numeriche spingono però ad utilizzare metodi sub-ottimi e che operano direttamente nel dominio logaritmico.
Siamo finalmente in grado di illustrare l’operatività della tecnica, con l’aiuto di fig.
17.34, in cui (come nel seguito) si adotta la notazione
L(m) per indicare tutti i valori
L(mj) per
j = 1, 2, ⋯, k:
- una prima decodifica siso1 considera nulla la verosimiglianza a priori ovvero La(m) = 0 (switch a massa), e in base a Lc in uscita dal canale, relativa ai bit di m e di c1 (prodotti dal primo rsc di codifica) ottiene la verosimiglianza a posteriori Lp1( m) e da questa l’informazione estrinseca Le1( m) = Lp1 − Lc che dipende solo dai valori di c1;
- il blocco siso2 adotta Le1( m) come valore della llr a priori La2( m) per i bit di messaggio m, dopo che l’interleaver ne ha posto i valori nello stesso ordine con cui si sono presentati a rsc2. Dato che Le1 dipende dai valori di c1 a cui siso2 non ha accesso, rappresenta effettivamente qualcosa in più. Siso2 esegue l’algoritmo di decodifica ottenendo Lp2( m) a partire da Lc(m), Lc(c2) e La2( m), e valuta Le2 = Lp2 − Lc − La2, che dipende solamente da c2;
- dopo essere stata di nuovo riordinata temporalmente, l’informazione Le2( m) viene fornita al blocco siso1 sull’ingresso a priori La1( m), in quanto anch’essa rappresenta qualcosa che siso1 non può calcolare per suo conto. Ecco così attuato il principio di controreazione! Ciò consente di ottenere dei nuovi valori per Lp1 e Le1 = Lp1 − Lc − La1;
- se i valori di Lp1 e Lp2 sono abbastanza simili per tutti gli indici j = 1, 2, ⋯, k i due rami sono collaborativamente addivenuti alla stessa conclusione, e la decodifica finale per tutti gli m̂j si ottiene dall’uscita Lp di uno dei due siso valutando se Lp≷0; altrimenti, si torna al passo 2. La tecnica descritta si è mostrata capace di convergere nel giro di una decina di iterazioni.
I turbo codici sono utilizzati, oltre che nei sistemi UMTS ed LTE, dagli standard DVB-RCS,
WiMax, e da missioni spaziali. Il principio della codifica turbo si applica non solo al caso accennato degli
rsc paralleli, ma può essere adottato anche per schemi seriali, e per
codici prodotto. Il blocco di codifica interno può altresì essere sostituito da un modulatore-demodulatore
con memoria, come ad es. il
tcm (pag.
1). In base alla stessa logica anche l’equalizzazione
mlsd di un canale con memoria (§
18.4.5) può beneficiare di uno schema turbo, in cui equalizzatore e decodificatore si scambiano iterativamente informazione estrinseca per addivenire ad una decisione condivisa.
17.5.2 Codifica a bassa densità di controllo parità
Questo approccio si basa su di un codice lineare
a blocchi caratterizzato da una una
matrice di controllo H con una
bassa densità di uni, da cui I’acronimo LDPC
(
low-density parity-check)
.
Riprendendo i concetti espressi al §
17.4.1, la moltiplicazione con somma modulo due
⊕ (pag.
1)
x = m ⋅ G tra il vettore
riga m dei
k bit di messaggio e la matrice binaria
G (detta
generatrice) con
k righe ed
n colonne produce una codeword
x di
n elementi. Se
G è posta nella forma
G = [Ik|P ] con
Ik matrice identità con
k righe e colonne e
P matrice
di parità di
k righe per
n − k colonne, il codice è detto
sistematico e le codeword possono esser scritte come
x = [ m1 ⋯ mk c1 ⋯ cn − k ] in cui
cj = ∑ki = 1⊕ mipij valuta la parità sui bit
mi per i quali
pij = 1.
Un codice
ldpc non è definito a partire da
G bensì dalla matrice
H di controllo di dimensione
(n − k) × n e che nel caso sistematico ha la forma
H = [PT|In − k ], ed in generale soddisfa la condizione (valida anche per un codice
non sistematico)
G ⋅ HT = 0k × (n − k)
in quanto ciascuna riga di
H è ortogonale ad ogni riga di
G; pertanto risulta
H ⋅ xT = 0Tn − k se e solo se
x è una codeword; mentre in presenza di errori il vettore ricevuto è
y ≠ x, e se il codice è sistematico il prodotto
H ⋅ yT ≠ 0 è detto
sindrome e viene usato per individuare i bit errati.
Precisiamo ora che le codeword
x di un codice
ldpc non fanno distinzione tra bit di messaggio
m e di parità
c, e sebbene il codice possa essere di tipo sistematico, è di gran lunga preferibile che non lo sia, per i motivi presto illustrati; questo fa si che la decodifica basata sulla sindrome non sia applicabile. Un modo per descrivere il funzionamento di un
ldpc è pensare che ogni riga
i di
H rappresenti il vincolo imposto sulle codeword da una tra
n − k equazioni di parità del tipo
∑nj = 1⊕ xjhij = 0
equivalente riga per riga dell’espressione
H ⋅ xT = 0.
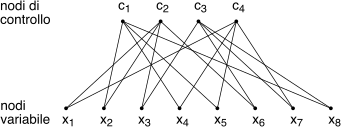
Esempio La matrice di controllo
H riportata sotto corrisponde alle quattro equazioni di vincolo scritte a fianco, che devono essere soddisfatte dai bit
xj delle codeword esenti da errore. Il codice risultante è descritto dai parametri
n, k = 8, 4 e da un tasso
Rc = 1⁄2.
H = ⎡⎢⎢⎣ 0 1 0 1 1 0 0 1 1 1 1 0 0 1 0 0 0 0 1 0 0 1 1 1 1 0 0 1 1 0 1 0 ⎤⎥⎥⎦
⎧⎪⎪⎨⎪⎪⎩ x2 ⊕ x4 ⊕ x5 ⊕ x8 = 0 x1 ⊕ x2 ⊕ x3 ⊕ x6 = 0 x3 ⊕ x6 ⊕ x7 ⊕ x8 = 0 x1 ⊕ x4 ⊕ x5 ⊕ x7 = 0
A parte il piccolo dettaglio di come poter effettuare la codifica x = m ⋅ G, per la matrice dell’esempio possiamo osservare che ogni bit xi compare in due equazioni, ed ogni equazione si applica a quattro bit. In generale un codice ldpc si dice regolare se presenta esattamente wc ≪ n − k elementi pari ad uno per ogni colonna, e wr = wcnn − k uni per ogni riga, a cui corrisponde un tasso Rc = k⁄n = 1 − wc⁄wr.
E’ il nome dato al grafo di cui
H è la matrice
di adiacenza, e che risulta essere tipo
bipartito ovvero i cui vertici si dividono in due insiemi, tra gli elementi dei quali non sono presenti archi. Si traccia (fig.
17.35) riportando
sotto i nodi (detti
variabile) associati agli
n bit ricevuti
xj, e
sopra quelli (
di controllo)
ci che verificano il rispetto delle equazioni di vincolo; tra questi nodi si traccia un arco tra
xj e
ci se è presente un
uno tra la riga
i e la colonna
j di
H, ovvero se
hij = 1.
In altre parole, i wc uni nelle n colonne rappresentano le connessioni dei nodi xj (ed infatti ne troviamo due) mentre i wr uni sulle n − k righe indicano le connessioni dei nodi ci (e ne troviamo quattro per ciascuno).
17.5.2.1 Decodifica iterativa
La particolarità più rilevante di un
ldpc è quella di svolgere la decodifica in modo
iterativo basandosi su di un ripetuto scambio di messaggi di natura probabilistica tra nodi-variabile e nodi di controllo, realizzando una applicazione di
propagazione della credenza nota anche come
algoritmo somma-prodotto. Lo scopo dell’algoritmo è individuare la codeword
x̂ = argmaxxp(x ⁄ y) che rende massima la prob. a posteriori (
pap) una volta noto il vettore
y in uscita dal canale. La ricerca è condotta attraverso un
raffinamento successivo di ipotesi, a partire dalla conoscenza dei valori
yj indipendenti che fornisce una
p(x ⁄ y) = ∏nj = 1p(xj ⁄ yj) di partenza.
Ad ogni iterazione ciascun nodo-variabile
j invia a tutti i
wc nodi di controllo
i(u),
u = 1, ⋯, wc a cui è connesso un messaggio
qji (pensiamo stia per
query) in cui comunica la
sua percezione della probabilità
pj di essere
pari ad uno. Ricevuti i messaggi
qji, ogni nodo di controllo
ci invia a ciascun nodo variabile
j(u),
u = 1, ⋯, wr a cui è connesso un messaggio
rji in cui
risponde con nuove stime di
pj ottenute combinando le opinioni
qji ricevute da tutti i nodi
tranne quello a cui è diretta la risposta. A questo punto i nodi-variabile generano nuovi messaggi
qji integrando la propria opinione di partenza con quella
rji ricevuta dai nodi di controllo, omettendo di includere l’informazione ricevuta da quello verso cui è diretto il messaggio. Il senso di omettere l’informazione proveniente dal destinatario è quello di attingere unicamente all’informazione
estrinseca, ossia non ricavabile autonomamente a destinazione, come avviene per i codici turbo.
L’opinione
di partenza sulla
pap pj che il bit
xj sia pari ad
1 è ottenuta (per ogni istante
j = 1, ⋯, n) a partire dal valore
yj in uscita dal canale come
pj = p(x = 1 ⁄ y) = p(y ⁄ x = 1)p(x = 1)p(y) = K ⋅ p(y ⁄ x = 1)
in cui
K = p(x = 1)p(y) = 1p(y ⁄ x = 1) + p(y ⁄ x = 0). A seconda se in presenza di un
bsc (§
17.1.1) oppure di un canale
soffice (o
awgn, pag.
1)
- bsc: il canale compie una decisione hard ed emette un valore y pari a zero od uno, con prob. condizionata in avanti p(y ⁄ x) di valore p(1 ⁄ 1) = p(0 ⁄ 0) = 1 − pe, p(0 ⁄ 1) = p(1 ⁄ 0) = pe. Dunque K = 1 sia per y = 1 che per y = 0, e p(x = 1 ⁄ y) = pe se y = 0 oppure 1 − pe quando y = 1 ;
- awgn: in funzione del valore binario di x ∈ {0, 1} il canale emette il valore continuo y = 2x − 1 + ε che è una v.a. gaussiana a valori indipendenti, media ±1 a seconda se x = 1 o 0, e varianza σ2; si ha quindi p(y ⁄ x) = 1√2πσexp⎧⎩− (y±1)22σ2⎫⎭.
In entrambi i casi, ogni nodo variabile j pone il messaggio iniziale qji = pj uguale per tutti gli i.
Calcolo ai nodi di controllo
Consideriamo ora un nodo ci che riceve più di un qji, e che sa che tra i nodi-variabile a lui collegati ci deve essere un numero pari di uni. Per ottenere il valore del messaggio rji da inviare indietro, ci somma le stime di probabilità ricevute.
Esempio Il nodo
c1 dell’esempio di fig.
17.35 deve far valere il vincolo
x2 ⊕ x4 ⊕ x5 ⊕ x8 = 0 ovvero nei quattro bit ci devono essere 4 uni, oppure due, oppure nessuno. Genera quindi il messaggio
r21 diretto a
x2 tenendo conto delle probabilità
qj1 ricevute da
x4,
x5 e
x6 e, considerandole
statisticamente indipendenti, stima
r21 = p̂2 = q41(1 − q51)(1 − q61) + (1-q41)q51(1 − q61) + (1-q41)(1-q51)q61 + q41q51q61
ossia pari a quella che ci sia un altro uno, oppure tre. Calcola quindi in modo analogo i messaggi r41 , r51 e r61 omettendo ogni volta di considerare l’informazione originata dal nodo destinazione.
Calcolo ai nodi-variabile
A questo punto ogni nodo-variabile j ha ricevuto wc messaggi rji, da cui ne calcola altrettanti da rispedire indietro, considerando oltre all’informazione p(0)j proveniente dal canale anche quella rji proveniente dai nodi ci, tranne quello di destinazione. Questa volta il calcolo di qji comporta il prodotto dei valori di probabilità ricevuti.
Esempio Il nodo x1 ha ricevuto r12 e r14, e valuta q12 = p(1)1 = k2p(0)1r14 da inviare a c2 in cui k2 = 1(1 − p(0)1)(1 − r14) + p(0)1r14 serve per normalizzare la stima, dato che se k2 non fosse presente p(1)2 risulterebbe più piccolo di tutti i valori ricevuti. In modo simile, il nodo x1 calcola poi q14 da inviare a c4 omettendo di usare r14.
Ad ogni ciclo
v = 1, 2, ⋯ si perviene ad una stima di probabilità
p̂(v)j che ogni bit
xj sia pari ad uno utilizzando
tutte le fonti informative, e da questa si ottiene una
ipotesi di codeword
x̃ operando per ogni bit una decisione
hard mediante una soglia di probabilità pari a
1⁄2. Se
x̃ soddisfa la condizione
H ⋅ x̃T = 0 allora è una codeword ammissibile, e la decodifica è terminata: in figura si mostra l’andamento
del numero di errori sul bit e del
peso della sindrome al progredire delle iterazioni. Se invece anche dopo un loro ragionevole numero la condizione non è mai verificata, significa che una eccessiva quantità di errori impedisce la decodifica corretta, e tale evenienza può essere segnalata agli stadi di elaborazione seguenti (particolare che non avviene per la decodifica
turbo).
17.5.2.2 Attenti a quel ciclo
Il calcolo svolto sia dai nodi di controllo che da quelli -variabile implica che gli eventi a cui si riferiscono i messaggi ricevuti siano statisticamente indipendenti. Ma se il grafo associato alla matrice H presenta cicli di lunghezza ν, dopo l’iterazione numero ν⁄2 l’ipotesi perde di validità, in quanto le stime di probabilità divengono dipendenti anche da quelle inviate dal nodo che le riceve.
In figura si evidenziano due cicli di lunghezza 4 presenti nel grafo di fig.
17.35, associati a quattro
uni disposti agli angoli di una sottomatrice rettangolare di
H. In fase di progetto della matrice di controllo tale circostanza va evitata, e dato che non è possibile non avere cicli, è bene vincolarne il numero e la lunghezza minima ad valore ritenuto adeguato a non degradare le prestazioni.
17.5.2.3 Implementazione Min-Sum
Il metodo esposto al §
17.5.2.1 comporta difficoltà legate a dover moltiplicare molti valori di probabilità, determinando instabilità numerica per dimensioni
n anche di decine di migliaia. Si preferisce allora lavorare nel dominio della verosimiglianza logaritmica (
llr), con un algoritmo del tutto simile a quello esposto, ma con alcune particolarità. Iniziamo con il definire la
llr della
pap di un bit
xj in perfetta analogia con la
(21.119), ovvero
L(xj ⁄ yj) = Lc(yj) + L(xj)
La decodifica iterativa ha ora l’obiettivo di aumentare
il modulo dalla
llr a priori L(xj) = ln p(xj = 1)p(xj = 0), inizialmente nullo, grazie all’apporto dell’informazione estrinseca proveniente dagli altri nodi.
Per quanto riguarda il contributo del canale Lc(yj) = ln p(yj ⁄ xj = 1)p(yj ⁄ xj = 0)
- nel caso awgn con mapping y = 2x − 1 + ε, in cui x ∈ {0, 1} e ε ∈ N(0, σ), si ha (vedi eq. (21.121)) Lc(yj) = 2σ2 y j;
- nel caso bsc con Pe = p risulta Lc(yj) = ln 1 − pp se yj = 1 ed Lc(yj) = ln p1 − p quando yj = 0.
In entrambi i casi si usa Lc(yj) per inizializzare i messaggi verso i nodi di controllo, che ora non valgono più qji ma L(qji) = ln Pr{xj = 1}1 − Pr{xj = 1}.
Per il calcolo della
llr dei messaggi
di risposta rji, il nodo
ci si auspica che la probabilità
pj = rji = Pr{xj = 1} sia uguale a quella che gli altri bit che partecipano al controllo svolto da
ci presentino un numero
dispari di uni, ossia
L(rji) = L⎛⎜⎝Pr⎧⎨⎩n⎲⎳j’ = 1
⊕, j’ ≠ jxj’hij’ = 1⎫⎬⎭⎞⎟⎠ = ln Pr{rji = 1}Pr{rji = 0}
Dopo una serie di sviluppi analitici di cui tralasciamo l’approfondimento, sotto l’ipotesi di indipendenza statistica si arriva ad esprimere
L(rji) in funzione approssimata della
llr L(qji) dei
qji da cui dipende, come
L(rji) ≈ ( − 1){∏ j’ ≠ j sgn(L(qj’i))} ⋅ min j’ ≠ j{|L(qj’i)|}
Il risultato si interpreta notando che il modulo (l’affidabilità) della
llr risultante
L(rji) è determinato dal
più piccolo dei moduli dei contributi
|L(qj’i)| (il meno affidabile), da cui l’appellativo di
Min a questo passaggio. Il segno positivo di
L(rji) indica poi che
Pr{rji = 1} > Pr{rji = 0} (o viceversa se negativo), e si ottiene come prodotto dei segni di
L(qj’i), indicando così una parità dispari o pari.
I nodi-variabile aggiornano le stime di
L(xj) come
L(xj) = Lc(yj) + ⎲⎳i L(rji)
da cui ottenere una ipotesi di codeword
x̃ con elementi
1 o
0 a seconda se
L(xj)≷0. Qualora
H ⋅ x̃T = 0 la decodifica è terminata; altrimenti si calcolano le
L(qji) = Lc(yj) + ⎲⎳i’ ≠ i L(rji’)
(passo
Sum) e si torna al passo
Min.
La natura probabilistica del metodo di decodifica non consente di ottenere una espressione in forma chiusa della Pe in funzione di Eb⁄N0, il cui grafico deve essere ottenuto mediante simulazione al computer ottenuta mediando su un gran numero di vettori ricevuti y: accade infatti che, sebbene il codice si comporti generalmente bene, per alcune configurazioni di partenza l’algoritmo di decodifica non riesca a convergere.
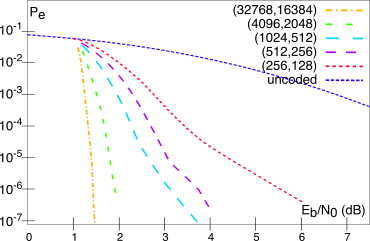
Di seguito sono riportate le prestazioni ottenute da un codice
ldpc regolare con
wc = 3 e
wr = 6,
Rc = 1⁄2, per una segnalazione antipodale su canale
awgn, con diverse scelte della lunghezza del blocco
n da 256 a 32768. A parte l’evidente guadagno rispetto alle prestazioni in assenza di codifica, i risultati possono essere confrontati con quelli di pag.
1 relativi al codice di Viterbi, e con il
limite di Shannon (§
17.3.4) che per un tasso
Rc = 1⁄2 fissa un requisito minimo pari a
Eb⁄N0 ≥ 0.188 dB,
mancato dal miglior codice esaminato solamente per un dB e mezzo.
Una alternativa per la matrice
H è quella che dà luogo ad un codice
irregolare, contraddistinto da un numero di uni per riga
wr(i) e per colonna
wc(j) non costanti, e che in generale consegue prestazioni
migliori di un codice regolare. In questo caso i bit
xj con
wc(j) più grande sono coinvolti in un maggior numero di vincoli e dunque la stima della loro probabilità diviene più affidabile; il miglioramento di verosimiglianza è quindi
distribuito in modo più
diffuso da parte dei nodi
ci con
wr(i) maggiore, in quanto collegati ad un maggior numero di nodi-variable. Tra i codici irregolari si menzionano quelli
quasi-ciclici e quelli
protografici, le cui matrici
H presentano una qualche struttura interna, che riduce la complessità del processo di co-decodifica.
Nel grafico di
Pe(Eb⁄N0) ottenuto dalle simulazioni si può distinguere la presenza di due regioni, la prima cosidetta di
waterfall (cascata) in cui oltre un certo valore di
Eb⁄N0 la
Pe decade piuttosto bruscamente, a cui fa seguito una regione
piattaforma (error floor) in cui la riduzione di
Pe è molto più graduale, se non nulla. Questo comportamento è attribuibile a
quasi-codeword ovvero sequenze
x̃ la cui sindrome
H ⋅ x̃T presenta un numero ridotto di uni, e che determina una situazione di
minimo locale per il processo di decodifica. In genere l’error floor si manifesta
prima per i codici con andamento
più ripido nella regione di waterfall (come quelli irregolari), sussistendo una situazione di compromesso tra le due esigenze.
Il numero di iterazioni necessario per arrivare alla decodifica corretta diminuisce all’aumentare di
Eb⁄N0, della dimensione del blocco
n, e del tasso
Rc, ed è possibile tenerne conto nel fissare il numero massimo di iterazioni prima di dichiarare un fallimento.
Rispetto ai turbo codici gli ldpc hanno il vantaggio che
- la decodifica può essere parallelizzata;
- sono più adatti alle velocità di trasmissione elevate;
- l’error floor si presenta per valori di Pe inferiori;
- resistono meglio agli errori a pacchetto;
- non è necessario alcun interleaver;
- uno stesso codice ldpc è adatto per diversi tipi di canale.
Tra gli svantaggi si citano
- una maggior complessità del codificatore;
- la realizzazione hardware può essere grande e ingombrante;
- un turbo codice si comporta meglio per lunghezze di blocco n più brevi e per tassi Rc minori.
Il successo della codifica ldpc ha portato alla sua adozione nelle ultime generazioni di standard: dopo la tv satellitare dvb-s2 (2005) viene adottata anche per la diffusione terrestre (dvb-t2) e via cavo (dvb-c), secondo un schema concatenato con ldpc come codice interno e bch esterno in modo da poter gestire il fenomeno dell’error floor.
E’ inoltre adottata per i collegamenti a microonde Wi-MAX 802.16, per le reti wireless WiFi 802.11n, per collegamenti Ethernet 10GBase-T su cavo ritorto, per reti domestiche G.hn con distribuzione su linee elettriche, telefoniche e coassiali fino a 1 Gbit/s (ITU G.9960, 2009), nonchè nel sistema televisivo terrestre dtmb della repubblica popolare cinese, e nella telefonia 5g.