9.1 Codifica di sorgente discreta
Iniziamo l’analisi considerando una sorgente di informazione che produce sequenze x(n) composte da simboli xk appartenenti ad un alfabeto di cardinalità L (ossia con k = {1, 2, ⋯, L}), e che si presentano con probabilità pk = Pr(xk) non dipendente da n, ovvero la sorgente è stazionaria.
Con questo termine si intende che i simboli vengono emessi in modo
statisticamente indipendente (§
6.1.5), ovvero indicando con
xh, xk una coppia di simboli consecutivi (ossia
x(n) = xh,
x(n + 1) = xk), la probabilità del secondo non dipende dall’identità del primo, ossia
p(xk ⁄ xh) = p(xk) = pk.
La conoscenza di ognuno dei simboli emessi
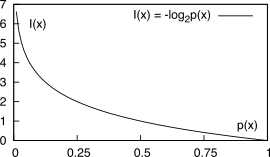
xk apporta una quantità di informazione (espressa in
bit) definita come
che rappresenta il
livello di dubbio a riguardo del verificarsi
dell’evento
xk prima che questo si verifichi, ovvero di quanto possiamo ritenerci sorpresi nel venire a conoscenza dell’evento
xk, di cui riteniamo di conoscere la probabilità
pk. Osserviamo infatti che la
(10.216) attribuisce un valore di informazione tanto più elevato quanto minore è la probabilità di emissione del simbolo.
La scelta di esprimere la relazione tra probabilità e informazione mediante il logaritmo in base 2 consente di verificare le seguenti osservazioni:
Notiamo inoltre che, essendo la sorgente senza memoria, due simboli emessi consecutivamente sono statisticamente indipendenti ovvero
p(xhxk) = p(xh)p(xk) e dunque
I(xh, xk) = − log2phpk = − log2ph − log2pk = I(xh) + I(xk)
Come in termodinamica al concetto di entropia si associa il grado di
disordine in un sistema, così per una sorgente informativa l’entropia misura il livello
medio di
casualità dei simboli emessi. Definiamo infatti
entropia (indicata con
H) di una sorgente discreta
S il valore atteso (§
6.2.2) della quantità di informazione apportata dalla conoscenza dei simboli (scelti tra
L possibili) da essa generati
che, pesando in probabilità la quantià di informazione associata ai diversi simboli, rappresenta il
tasso medio di informazione per simbolo espresso dalle sequenze osservabili. Come dimostriamo sotto, da tale definizione ne consegue che
- se i simboli sono equiprobabili (pk = 1L con ∀k) la sorgente è massimamente informativa, e la sua entropia è la massima possibile per un alfabeto ad L simboli, pari a HsMax = 1L ∑Lk = 1log2L = log2L bit/simbolo;
- se i simboli non sono equiprobabili, allora Hs < log2L;
- se la sorgente emette sempre e solo lo stesso simbolo, allora Hs = 0.
Questi predicati possono essere riassunti dall’espressione
Dimostrazione Osserviamo innanzitutto che
Hs ≥ 0 in quanto la
(10.217) comprende tutti termini positivi o nulli, essendo
log2α ≥ 0 per
α = 1⁄pk ≥ 1. Mostriamo ora che
Hs − log2L ≤ 0: riscriviamo innanzitutto il primo membro della diseguaglianza come
dato che
∑kpk = 1, ove le sommatorie su
k si intendono da
1 ad
L . Esprimiamo poi questo risultato parziale nei termini di logaritmi
naturali, tenendo conto che
log2 α = ln αln 2, ovvero
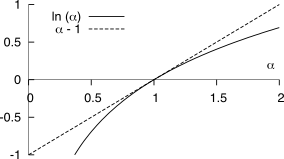
A questo punto utilizziamo
la relazione
ln α ≤ α − 1 mostrata in figura, con l’uguaglianza valida solo se
α = 1. Ponendo quindi
α = 1 L ⋅ pk e sostituendo la
(10.220) nella
(10.219) si ottiene
Hs − log2L = 1 ln 2 ⎲⎳k pkln 1 L ⋅ pk ≤ 1 ln 2 ⎲⎳k pk⎛⎝1 L ⋅ pk − 1⎞⎠ = = 1 ln 2 ⎛⎝⎲⎳k 1 L − ⎲⎳k pk⎞⎠ = 1 ln 2 (1 − 1) = 0
con il segno di uguale solo se
1L ⋅ pk = 1 ovvero
pk = 1L ⋅ .
9.1.1.1 Entropia di sorgente binaria
Nel caso particolare di una sorgente
binaria, ovvero che emette uno tra due simboli
{x0, x1} con probabilità rispettivamente
p0 = p,
p1 = q = 1 − p, la formula dell’entropia
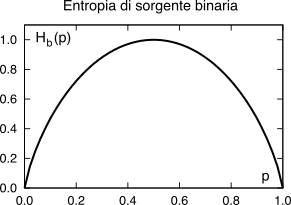
(10.217) fornisce l’espressione
il cui grafico è mostrato al lato sinistro di figura
9.2, in funzione di
p.
I due simboli {x0, x1} possono essere rappresentati dalle 2 cifre binarie {0, 1}, che in questo caso chiamiamo binit, per non confonderli con la misura dell’informazione (il bit). Osserviamo quindi che se p ≠ 0.5 si ottiene Hb(p) < 1, ossia la sorgente emette informazione con un tasso inferiore a un bit/simbolo, mentre a prima vista non potremmo usare meno di un binit per rappresentare ogni simbolo binario.
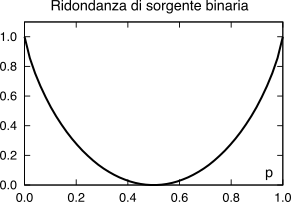
Esprime la differenza
D tra l’entropia di una sorgente
Hs (10.217) ad
L simboli ed il numero di binit
M = ⌈log2L⌉ necessario a rappresentarli, divisa per quest’ultimo, ovvero
mostrata sempre in fig.
9.2 per il caso
L = 2 al variare di
p. Esempio Consideriamo un sorgente binaria con p0 = 0.8 (e p1 = 0.2). L’applicazione della (10.221) fornisce un valore Hb(0.8) = 0.8 log2 10.8 + 0.2 log2 10.2 = 0.72 bit/simbolo, minore del valore di 1 bit/simbolo che si sarebbe ottenuto nel caso di equiprobabilità. La relativa ridondanza D è pari a 1 − 0.72⁄1 = 0.28, ovvero il 28 %.
9.1.1.3 Entropia di sorgente L-aria
L’applicazione della
(10.218) al caso di una sorgente che emette simboli
non equiprobabili ed appartenenti ad un alfabeto di cardinalità
L, determina per la stessa un valore di entropia
HL < log2L bit/simbolo.
Esempio Nel caso di una sorgente quaternaria con p0 = 0.5, p1 = 0.25, p2 = 0.125, p3 = 0.125, l’applicazione della (10.217) fornisce H4 = 1.75 bit/simbolo, inferiore ai 2 bit/simbolo di una sorgente con quattro simboli equiprobabili. La relativa ridondanza è ora pari a 1 − 1.75⁄2 = 0.125 ovvero il 12.5 %.
9.1.2 Intensità informativa e codifica binaria
Svolgiamo ora alcune considerazioni relative alla possibilità di ridurre la ridondanza mediante una operazione di
codifica (di sorgente). Consideriamo una sorgente discreta senza memoria con alfabeto ad
L simboli, caratterizzata da una entropia di
Hs bit/simbolo, e che emette i valori
xk a frequenza
fs simboli/secondo: il
flusso informativo risultante consegue quindi una
intensità o
velocità di informazione pari a
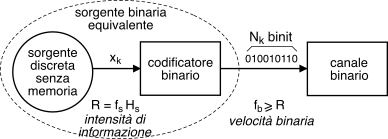
Volendo trasmettere tale informazione attraverso un
canale binario (vedi §
17.1.1), l’elemento indicato in figura come
codificatore binario fa corrispondere ad ogni simbolo
xk un numero variabile di
Nk binit, scelti in modo da utilizzare meno binit per i simboli più probabili (e più binit per quelli
rari) come descritto nel seguito, producendo una
velocità di trasmissione binaria di
fb binit⁄sec. Dal punto di vista del canale il messaggio è prodotto da una nuova sorgente
equivalente, i cui simboli binari hanno probabilità
p e
1 − p, e dunque caratterizzata da una entropia
Hb(p) bit⁄binit ≤ 1. Dato che l’intensità informativa in ingresso
fs ⋅ Hs ed in uscita
fb ⋅ Hb(p) dal codificatore deve essere la stessa e che
Hb(p) ≤ 1, la velocità binaria
fb della sorgente binaria equivalente rispecchia il vincolo
Il rapporto
N = fb fs ≥ Hs rappresenta il numero
medio di binit emessi per ciascun simbolo della sorgente, e può essere valutato a partire dalle probabilità
pk dei simboli
xk e dal numero
Nk di binit necessario a rappresentarlo, come valore atteso
N = E{Nk} = ∑kpkNk.
9.1.2.1 Teorema della codifica di sorgente
Noto anche come
primo teorema di Shannon, afferma che
esiste un modo di scegliere gli
Nk binit associati a ciascun simbolo
xk tale che
con
ϵ piccolo a piacere, e che si annulla in corrispondenza della codifica
ottima, per la quale risulta
N = Hs. Ma non dice come fare, cosa di cui ci occupiamo ai §§ seguenti.
9.1.2.2 Codebook e codeword
Le operazioni svolte dal codificatore binario sono descritte nei termini della emissione di una parola di codice detta anche codeword, prelevata da un dizionario (o codebook) che descrive la collezione di tutte le possibili codeword.
9.1.2.3 Efficienza del codice
E’ la misura
η di quanti bit di informazione sono trasportati da ogni binit di codifica, ed è definita come il rapporto tra l’entropia di sorgente
Hs bit⁄simbolo ed il numero medio
N di
binit⁄simbolo emessi: in base alla
(10.223) ed alla considerazione che
fb = fs ⋅ N si ottiene
e pertanto
η è anche pari al rapporto tra gli
R bit⁄secondo di informazione della sorgente e la velocità di trasmissione
fb binit⁄secondo prodotta dal codificatore.
Osservazione All’aumentare dell’efficienza, si assiste ad una contemporanea riduzione della ridondanza, potendo scrivere η + D = 1.
Sappiamo già che qualora i binit emessi a velocità
fb assumano i valori 0 o 1 in modo equiprobabile, allora per la sorgente equivalente risulta
Hb⎛⎝12⎞⎠ = 1, ovvero dalla
(10.224) fb = R e dalla
(10.226) N = Hs. Dunque il problema di individuare un codice ottimo diviene quello di trovare un insieme di
codeword tali da rendere
equiprobabili i valori dei binit, con il vincolo di mantenere il codice
decifrabile, ovvero tale da rispettare la
regola del prefisso. Ma andiamo con ordine.
9.1.3 Codifica con lunghezza di parola variabile
Mostriamo mediante un esempio
come scegliendo codeword
più lunghe per rappresentare i simboli
meno probabili, e
più corte per i simboli
più frequenti, si può subito ottenere una migliore efficienza del codice. Consideriamo infatti la sorgente del secondo esempio a pag.
1, con alfabeto di cardinalità
L = 4, ai cui simboli competono le probabilità riportate alla seconda colonna della tabella. In questo caso l’entropia vale
Hs = ⎲⎳k pklog2 1pk = = 1 2 log22 + 1 4 log24 + 2 8 log28 = 1 2 + 1 2 + 2 8 ⋅ 3 = 1.75 bit ⁄simbolo
Se il codificatore di sorgente adotta le codeword mostrate nella terza colonna, a cui corrispondono le lunghezze di
Nk binit riportate nella quarta colonna, il numero
medio di binit/simbolo prodotti dalla codifica binaria risulta pari a
Con queste codeword otteniamo dunque
Hs = N, ovvero una efficienza
η = 1! Intraprendiamo allora un ragionamento che ci porterà a concludere come questo sia un risultato per nulla scontato, e che dipende sia dalla particolare scelta fatta per le codeword, sia dal particolare tipo delle
pk dell’esempio, tutte potenze negative di due (essendo
0.5 = 2−1,
0.25 = 2−2,
0.125 = 2−3).
9.1.3.1 Regola del prefisso
Affinché un insieme di codeword di lunghezza variabile possa assere adottato come
codebook di sorgente, queste devono poter essere riconosciute come
distinte presso il ricevitore, e ciò è possibile a patto che nessuna sia
uguale all’inizio di una codeword più lunga. Si può mostrare che la condizione necessaria e sufficiente per avere un codice
non ambiguo è che il numero di binit
Nk con cui sono espresse le codeword soddisfi la
disuguaglianza di Kraft, espressa come
Esempio Nella tabella sono riportati quattro possibili codici
(
A,B,C,D) per la sorgente quaternaria già discussa, assieme al corrispettivo valore di
N e
K. Il codice
A corrisponde ad un codificatore particolarmente banale con
Nk = N per tutti i
k, dunque la
(10.228) diviene
K = L 2 − N ≤ 1 ed è soddisfatta a patto che
N ≥ log2L: nel nostro caso, essendo
L = 4 ed
N = 2, si ottiene
log2 L = 2 = N e quindi
K = 1, dunque il codice è decifrabile (anche perché a lunghezza fissa), ma non particolarmente valido, in quanto l’efficienza espressa dalla
(10.226) risulta pari a η = Hs N = 1.752 = 0, 875 < 1. Ma quando
Hs < log2L come nel nostro caso, si può realizzare una efficienza migliore ricorrendo ad un codice a lunghezza variabile.
Le codeword del codice
B producono un valore
K = 1.5 > 1, e dunque rappresentano un codice ambiguo: difatti, violano la regola del prefisso. Il codice
C invece non è ambiguo , essendo
K < 1, ma presenta una efficienza
Hs N = 0, 93 < 1 e dunque è anch’esso sub-ottimale. Infine, il codice
D è quello analizzato al precedente paragrafo, ed effettivamente risulta una scelta
ottima, dato che oltre a soddisfare la
(10.228), consegue una efficienza
Hs N = 1.
Indichiamo con questo termine un codice che oltre a soddisfare la regola del prefisso consegue anche una efficienza
(10.226) unitaria, ovvero
Hs N=1. Perché ciò avvenga il valore
pk delle probabilità di simbolo
deve essere una potenza negativa di due, ovvero
pk = 2 − Nk con
Nk intero: in tal caso la
(10.228) si scrive
K = ∑Lk = 1 2 − Nk = ∑Lk = 1 pk = 1 e la diseguaglianza di Kraft è verificata con il segno di uguale, dunque è possibile individuare un codice non ambiguo.
Osserviamo inoltre che scegliendo la lunghezza delle codeword proprio pari a
Nk = log2 1pk, l’espressione
(10.227) che ne calcola la lunghezza media
N = ∑k pkNk coincide con quella
(10.217) che fornisce
Hs = ∑k pklog2 1pk, ovvero ogni simbolo è codificato con una codeword lunga tanti binit quanti sono i bit di informazione che trasporta, determinando una efficienza
η unitaria. Per individuare un codice che
si avvicini a questa proprietà si può utilizzare la tecnica di
Huffman presentata appresso, mentre per
modificare le
pk si ricorre alla
codifica per blocchi di simboli esposta al §
9.1.4.
9.1.3.3 Codice di Huffman
E’ basato su di un algoritmo capace di individuare un codice a lunghezza variabile che soddisfa la regola del prefisso, adotta codeword più lunghe per i simboli meno probabili, e tenta di rendere equiprobabili le cifre binarie che compongono le codeword. L’algoritmo definisce un albero binario i cui rami sono etichettati con 1 e 0, che può essere realizzato attuando i seguenti passi:
- crea una lista contenente i simboli della sorgente, ordinati per valore di probabilità decrescente, ed associa ad ognuno di essi un nodo-foglia dell’albero;
- finché c’è più di un nodo nella lista:
- rimuovi dalla lista i due nodi con la probabilità più bassa;
- crea un nuovo nodo interno all’albero con questi due nodi come figli, e con probabilità pari alla somma delle loro probabilità;
- aggiungi il nuovo nodo alla lista, in ordine di probabilità;
- il nodo rimanente è la radice, e l’albero è completo;
- assegna cifre binarie diverse ad ogni coppia di rami a partire dalla radice, concatenando le quali si ottengono le codeword per i simboli sulle foglie
Si può dimostrare che il codice di Huffman generato in questo modo è il migliore possibile nel caso in cui la statistica dei simboli di sorgente sia nota a priori, nel senso che produce un codebook con il minor numero possibile di binit/simbolo medi
N, e le cui codeword allo stesso tempo soddisfano la regola del prefisso e la disuguaglianza di Kraft. La codifica di Huffman è ampiamente utilizzata nel contesto di altri metodi di compressione (metodo
deflate di
pkzip, §
9.2.3) e di codec multimediali (
jpeg e
mp3, cap.
10), in virtù della sua semplicità, velocità, ed assenza di brevetti.
Ovviamente ci deve essere un accordo a priori tra sorgente e destinatario a riguardo della corrispondenza tra parole di codice e simboli (o blocchi di simboli) della sorgente. Nel caso in cui ciò non sia vero, oppure nel caso in cui la statistica dei simboli della sorgente sia stimata a partire dal materiale da codificare, occorre inviare all’inizio della comunicazione anche la tabella di corrispondenza, eventualmente in forma a sua volta codificata.
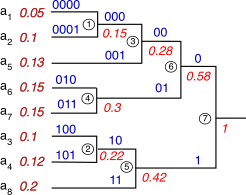
Esempio Una sorgente con
L = 8 simboli è caratterizzata dalle probabilità di simbolo riportate alla figura seguente, a partire dalle quali si realizza un codice di Huffman mediante la costruzione grafica riportata, in cui le probabilità sono scritte
in rosso,
sotto i rami ed accanto ai simboli, mentre i binit
sopra i rami,
in blu.
Dopo aver ordinato i simboli in base alle probabilità, si
individuano i due nodi con probabilità più bassa come
a1 e
a2, che assommano prob. 0.15 e sono etichettati come nodo ➀; dunque la coppia ora meno probabile è
a3 con
a4, che cumula prob. 0.22 e si etichetta ➁. Quindi, le due prob. minori divengono quelle del nodo ➀ e del simbolo
a5, che assommano a 0.28 generando il nodo ➂; il passo successivo è quello di accoppiare
a6 con
a7 generando il nodo ➃ a cui compete la prob. di 0.3. Gli ultimi tre passi vedono accoppiare ➁ con
a8 producendo ➄ con prob. 0.42, quindi ➂ con ➃ generando ➅ con probabilità 0.58, ed infine ➄ con ➅ producendo il nodo radice a cui compete una prob. unitaria. Si può ora procedere, partendo dalla radice a destra, ad assegnare un binit pari a 0 o 1 ad ogni coppia di rami rispettivamente in alto ed in basso, ripetendo l’assegnazione seguendo le diramazioni verso sinistra, sopra le quali sono mostrate le codeword che si formano, di cui l’inizio in comune replica la configurazione assegnata al padre. Le codeword complete che compaiono sui rami più a sinistra sono quindi riportate alla terza colonna della tabella. Come è possibile verificare, il codice rispetta la regola del prefisso, in quanto nessuna delle codeword è uguale all’inizio di altre.
Osservazioni Se calcoliamo Hs, N e η per la sorgente ed il codice individuato, si ottiene Hs = 2.916, non molto meno del massimo log2L = 3 bit a simbolo, corrispondente a probabilità pk tutte uguali e pari a 1⁄8 = 0.125. Il codice consegue una lunghezza media di codeword pari a N = 2.95, e come osserviamo usa 3 binit per i 5 simboli con probabilità intermedia, il 15% delle volte usa 4 binit, ed il 20% due. Il codice consegue pertanto una efficienza η = Hs⁄N = 0.988, ovvero la sorgente codificata presenta una ridondanza D solamente del 1,2%.
9.1.3.4 Codifica dinamica (di Huffman)
L’esecuzione dell’algoritmo di Huffman richiede la preventiva stima della probabilità pk dei simboli, ottenuta a partire dal messaggio da codificare; inoltre, prima di trasmettere il messaggio codificato occorre inviare anche il codebook prodotto dall’algoritmo, per permettere al decodificatore di funzionare.
La variante adattiva dell’algoritmo di generazione del codice prevede invece di utilizzare valori pk stimati durante l’analisi del messaggio, con quelle p̂k costruire l’albero, e con l’albero corrente codificare i simboli man mano che vengono presi in considerazione. Durante l’analisi e la codifica del messaggio le p̂k si modificano, con esse l’albero, ed il codice. Lo stesso algoritmo adattivo è implementato anche al ricevitore, che sviluppa dal suo lato il medesimo albero, evitando così di dover trasmettere il codebook, e permettendo di adottare la tecnica anche per messaggi prodotti in tempo reale. Inoltre, nel caso in cui il messaggio non sia propriamente stazionario e le pk non si mantengano costanti nel tempo, l’adattività consente al codice di seguire tale variazioni e di conseguire in tal caso prestazioni anche migliori della tecnica statica.
9.1.4 Codifica per blocchi
Riprendiamo la discussione iniziata a pag.
1 relativa al codice binario ottimo per una sorgente
L − aria senza memoria con simboli
xk a probabilità
pk, notando che se la lunghezza
Nk della codeword associata ad
xk viene scelta in modo tale che
si può mostrare che la disuguaglianza di Kraft
(10.228) è soddisfatta , e dunque è possibile realizzare un codice
non ambiguo con tali codeword. Moltiplicando ora i membri di
(10.229) per
pk e sommando su
k si ottiene
da cui si deduce che è possibile ottenere un’efficienza
η = Hs N → 1 solo se
Hs≫1, oppure se
Nk ≃ log2 1pk (vedi nota
467).
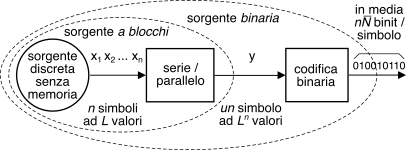
Ma esiste anche un’altra possibilità: quella di raggruppare i simboli
xk in blocchi
di
n elementi, e considerare l’intero blocco come un
unico simbolo di una nuova sorgente equivalente con alfabeto a
Ln valori, come rappresentato in figura. Essendo la sorgente senza memoria i suoi simboli sono indipendenti, e quindi si dimostra che l’entropia della nuova sorgente è
n volte quella originale, ossia
Hbloccos = nHs. Il risultato
(10.230) quindi ora si scrive come
nHs ≤ nN ≤ nHs + 1 in cui
nN è il numero medio di binit
per blocco, e dividendo per
n, otteniamo infine
che rappresenta una forma di dimostrazione del teorema
(10.225) con
ϵ = 1 n, e che permette di ottenere
N → Hs se
n → ∞, avvicinandosi alle condizioni di codifica ottima per qualsiasi distribuzione delle
pk.
Esercizio Per applicare questo metodo ad un caso pratico, consideriamo una sorgente
binaria senza memoria che emette simboli
xk con probabilità
pk mostrata in tabella. Per ogni coppia di simboli il blocco serie/parallelo
della fig. precedente emette un simbolo quaternario
yh a cui (in virtù dell’indipendenza statistica tra i simboli
xk) compete la probabilità ottenuta moltiplicando le probabilità della coppia
xixj associata. Codifichiamo quindi i simboli
yh con il codice a lunghezza variabile introdotto al §
9.1.3 , e ricalcoliamo il numero medio di binit/simbolo
N, che risulta pari a
N = 1 ⋅ 0.64 + 2 ⋅ 0.16 + 3 ⋅ 0.16 + 3 ⋅ 0.04 = 1.58 binit
ogni 2 simboli, ossia pari ad una media di 0.79 binit/simbolo binario, mentre in assenza di codifica a blocchi non avremmo potuto utilizzare meno di 1 binit/simbolo binario. Al crescere della dimensione di blocco
n si può verificare come
N si avvicini sempre più al valore dell’entropia della sorgente binaria
Hb = 0.72 calcolato a pag.
1, ovvero dimostrare l’eq.
(10.231).
9.1.4.1 Compromesso velocità-ritardo
Come indicato dalla
(10.231), realizzando blocchi via via più lunghi è possibile ridurre la
velocità media di codifica
N ⋅ fs (in binit/sec) rendendo
N sempre più vicino all’entropia, ovvero
min [N] = Hs + ε
in cui
ε → 0 se la lunghezza n del blocco tende ad infinito. D’altra parte, all’aumentare della dimensione del blocco aumenta di egual misura il ritardo che intercorre tra l’emissione di un simbolo e la sua codifica, e di questo va tenuto conto, nel caso sussistano dei vincoli temporali particolarmente stringenti sulla consegna del messaggio. Qualora una sorgente discreta ad
L simboli esibisca un valore di entropia inferiore a
log2L, la velocità binaria
N ⋅ fs in uscita dal codificatore di sorgente può essere ridotta e resa prossima all’intensità informativa
R (eq.
(10.223)) adottando una codifica a blocchi di lunghezza via via crescente, e utilizzando per i nuovi simboli compositi un opportuno codice di Huffman.
Esercizio Sperimentare la costruzione di un codice di Huffman basato sul raggruppamento di tre simboli della sorgente binaria dell’esercizio precedente, e verificare se il numero medio di binit/simbolo binario N riesce ad avvicinarsi ancora di più al valore dell’entropia della sorgente binaria pari a 0.72 bit/binit.