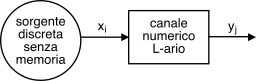
17.1 Dove arrivare, e come partire
E’ più che lecito chiedersi ora di quanto si possa ridurre la
Pe, e quanta ridondanza sia necessario aggiungere. La teoria che affronteremo risponde che finché l’intensità informativa
R = fs ⋅ Hs in uscita dal codificatore di sorgente (eq.
(10.223)) si mantiene inferiore al valore della
capacità di canale C (§§
17.2 e
17.3), l’informazione può essere trasportata (teoricamente)
senza errori! Mentre se al contrario
R > C, non è possibile trovare nessun procedimento in grado di ridurre gli errori - che anzi, divengono praticamente
certi. Infine (pur senza spiegare come fare) la teoria assicura che la ridondanza che occorre aggiungere può essere resa
trascurabile! Ma prima di approfondire questi risultati a dir poco fenomenali, svolgiamo alcune riflessioni su come
- la probabilità ed il tipo di errori introdotti da un canale numerico possono essere descritti, noto l’ingresso, nei termini di una matrice di probabilità di transizione;
- la decisione relativa al simbolo trasmesso si può basare, oltre che sulla conoscenza di tale matrice, anche sulle probabilità di come sono emessi i simboli della sorgente;
- al verificarsi di errori corrisponde una perdita di informazione.
17.1.1 Canale binario simmetrico
Mentre al §
15.4 si è sviluppato un lungo ragionamento per arrivare ad un valore di probabilità di errore (eq.
(21.21)), in questa sede ci riferiamo al solo risultato finale,
il valore
Pbite = p che caratterizza il
modello raffigurato a lato e descritto dal termine
bsc o
binary symmetric channel che rappresenta appunto un canale numerico
binario con probabilità
p di introdurre errore,
indipendentemente dal simbolo di ingresso, e per questo
simmetrico.
In termini più formali indichiamo con x1 e x2 i due possibili ingressi e, qualora (con prob. 1 − p) non si verifichi errore, con y1 e y2 le rispettive uscite, mentre in presenza di errore (con probabilità p), in uscita si presenta il simbolo opposto.
Qualora i simboli di ingresso
x1 e
x2 non siano equiprobabili, indichiamo con
α e
1 − α le relative prob. a priori (§
6.1.4).
Individuano le probabilità condizionate pji = p(yj ⁄ xi) di osservare yj in uscita quando in ingresso è presente xi, e per questo dette in avanti.
I suoi elementi sono le prob.
pji, e nel caso
bsc la matrice è
simmetrica in quanto
⎧⎨⎩ p(y2 ⁄ x1) = p(y1 ⁄ x2) = p p(y1 ⁄ x1) = p(y2 ⁄ x2) = 1 − p ovvero Π = [pji] = ⎡⎢⎣ 1 − p p p 1 − p ⎤⎥⎦
Osserviamo due cose: la prima è che le prob. py = (p(y1), p(y2))⊤dei simboli di uscita si calcolano come py = Π ⋅ px; la seconda è che le definizioni date si estendono immediatamente al caso di canale L − ario, come nel caso multilivello.
17.1.2 Decisione a verosimiglianza ed a posteriori
Il simbolo
yi in uscita dal canale numerico
non è una variabile aleatoria, bensì una osservazione effettiva, e la decisione su quale
xj l’abbia prodotto avviene secondo un procedimento di
verifica di ipotesi (§
6.6.1), basata sul valore assunto da un rapporto tra valori di probabilità.
Decisione di massima verosimiglianza
Qualora siano note solamente le probabilità in avanti
pij ma non quelle a priori, la decisione avviene sulla base del
rapporto di verosimiglianza (§
6.6.2). Supponiamo che l’uscita del
bsc sia ad es. il valore
y1: la decisione su quale delle ipotesi
x1 od
x2 sia più probabile in questo caso avviene in base al rapporto
RML tra le probabilità
in avanti, e prende il nome di decisione di
massima verosimiglianza (vedi §
6.6.2.1) o
Maximum Likelihood, ovvero
decidendo quindi per l’ipotesi
più verosimile in funzione del valore maggiore o minore di uno per
RML. Nel caso risulti
p < 12 la regola
(21.85) equivale a scegliere l’ingresso concorde con l’uscita, oppure l’opposto se
p > 12 (!). Qualora invece si riceva
y2, il rapporto e la relativa regola di decisione sono definiti come
RML(y2) = p(y2 ⁄ x2)p(y2 ⁄ x1) x2 ↑ ≷ ↓ x1 1. Nel caso di trasmissione
L − aria, infine, la ricezione di
yj porta alla decisione per
xi:i = argmaxi = 1, 2, ⋯L{p(yj ⁄ xi)} Decisione di massima probabilità a posteriori (MAP)
Conoscendo anche le probabilità
a priori p(x1) e
p(x2), se i due simboli
x1 ed
x2 non sono equiprobabili, la decisione può avvenire confrontando le probabilità
a posteriori p(xj ⁄ yi), calcolabili applicando il teorema di Bayes (vedi §
6.1.4). Facendo di nuovo il caso di aver ricevuto il simbolo
y1, scriviamo dunque
o più in generale, comprendendo anche il caso di canale
L − ario, il criterio di decisione
map qualora si riceva
yi è espresso come
xi : i = argmaxi = 1, 2, ⋯L{p(yj ⁄ xi)p(xi)}
Il modo con cui le probabilità
a priori p(x1) e
p(x2) correggono la decisione
ml (21.85) in
map (21.86) per un
bsc si presta a due osservazioni
- x1 potrebbe essere così raro che, in presenza di una moderata probabilità di errore, si preferisce decidere sempre x2, attribuendo l’eventuale ricezione di y1 ad un errore del canale, piuttosto che all’effettiva trasmissione di x1.
- in assenza di canale (ossia senza ricevere nulla) l’unica decisione possibile si basa sul confronto tra le p. a priori p(x1) e p(x2). La ricezione di un simbolo yi apporta nuova informazione, alterando il rapporto di decisione R in misura tanto maggiore quanto minore è la probabilità di errore.
Esempio Verifichiamo le ultime osservazioni esplicitando una probabilità a posteriori in funzione di
p:
p(x1 ⁄ y1) = p(x1, y1)p(y1) = p(y1 ⁄ x1)p(x1)p(y1 ⁄ x1)p(x1) + p(y1 ⁄ x2)p(x2) = = (1 − p) ⋅ p(x1)(1 − p) ⋅ p(x1) + p ⋅ p(x2) = p(x1)p(x1) + p1 − pp(x2)
Se
p = 1 − p = 12, il canale
è inservibile e non trasferisce informazione: infatti si ottiene
p(x1 ⁄ y1) = p(x1) pari a quella a priori, in quanto
p(x1) + p(x2) = 1. D’altra parte se
p < 12 si ottiene
p(x1 ⁄ y1) > p(x1) dato che ora
p1 − p < 0.5: si assiste pertanto ad un
aumento della probabilità di
x1 rispetto a quella a priori; se poi la probabilità di errore tende a zero (
p → 0) si ottiene
p(x1 ⁄ y1) → 1.
17.1.3 Informazione mutua media per canale numerico L − ario
Approfondiamo questa nozione introdotta al §
9.4.3 e li utilizzata per definire la funzione velocità distorsione (§
9.5.2), mostrando come
l’informazione condivisa tra ingresso ed uscita di un canale consenta di determinare anche la quantità di informazione che viene
persa a causa degli errori che si sono verificati.
Consideriamo una sorgente discreta che emette simboli
x appartenenti ad un alfabeto finito di cardinalità
L, ossia
x ∈ {xi} con
i = 1, 2, ⋯, L, ed indichiamo con
y ∈ {yj} (sempre per
j = 1, 2, ⋯, L) il corrispondente simbolo ricevuto mediante un canale discreto, in generale diverso da
x, a causa di errori introdotti dal canale. Conoscendo le densità di probabilità
p(xi),
p(yj), e le probabilità congiunte
p(xi, yj), possiamo definire la quantità di informazione
in comune tra
xi e
yj, denominata
informazione mutua, come
da cui deriva che
- se ingresso ed uscita del canale sono statisticamente indipendenti si ha p(xi, yj) = p(xi)p(yj), e di conseguenza l’informazione mutua è nulla;
- se p(yj ⁄ xi) > p(yj) significa che l’essere a conoscenza della trasmissione di xi rende la ricezione di yj più probabile di quanto non lo fosse a priori, e corrisponde ad una informazione mutua positiva;
- la definizione di informazione mutua è simmetrica, ovvero I(xi, yj) = I(yj, xi);
- rifrasando la 2. in virtù della 3., se p(xi ⁄ yj) > p(xj) allora ricevere yj rende la trasmissione di xi più probabile di quanto non lo fosse a priori, manifestando lo stesso valore di informazione mutua positiva del punto 2.
Per giungere ad una grandezza
I(X, Y) che tenga conto del comportamento
medio del canale, ovvero per coppie ingresso-uscita qualsiasi, occorre pesare i valori di
I(xi, yj) con le relative probabilità congiunte, ossia calcolarne il valore atteso rispetto a tutte le possibili coppie
(xi, yj):
ri-ottenendo così l’
informazione mutua media (§
9.4.3), misurata in bit/simbolo, e che rappresenta (in media) quanta informazione ogni simbolo ricevuto trasporta a riguardo di quello trasmesso. In virtù della simmetria di questa definizione, ci accorgiamo che il valore di
I(X, Y) può essere espresso nelle due forme alternative
in cui l’entropia
condizionale (
§ 9.4.2)
prende il nome di
equivocazione e rappresenta la quantità media di informazione
persa, rispetto all’entropia di sorgente
H(X), a causa della rumorosità del canale.
Nel caso in cui il canale non introduca errori, e quindi p(xi ⁄ yj) sia pari a 1 se j = i e zero altrimenti, è facile vedere che H(X ⁄ Y) è pari a zero, e I(X, Y) = H(X), ossia tutta l’informazione della sorgente si trasferisce a destinazione. D’altra parte
prende il nome di
noise entropy dato che considera il processo di rumore come se fosse un segnale informativo: infatti, sebbene si possa essere tentati di dire che l’informazione media ricevuta è misurata dalla entropia
H(Y) della sequenza di osservazione, una parte di essa
H(Y ⁄ X) è falsa, perché in realtà è introdotta dagli errori.
Calcolo dell’informazione mutua media per il BSC
Torniamo al caso binario descritto al §
17.1.1 ed usiamo la
(21.89) per calcolare l’informazione mutua media in funzione della probabilità a priori
p(x1) = α e di quella in avanti
pe, valutando innanzitutto
H(Y) e
H(Y ⁄ X). Dal punto di vista dell’uscita del canale, i simboli
y1,
y2 costituiscono l’alfabeto di una sorgente binaria senza memoria, la cui entropia si esprime in termini di
p(y1) mediante la
(10.221), ovvero
H(Y) = Hb(p(y1)), in cui
p(y1) = p(y1 ⁄ x1)p(x1) + p(y1 ⁄ x2)p(x2) = = (1 − pe)α + pe(1 − α) = pe + α − 2αpe
e dunque
H(Y) = Hb(pe + α − 2αpe). Per quanto riguarda la
noise entropy H(Y ⁄ X), sostituendo
p(xi, yj) = p(yj ⁄ xi)p(xi) nella
(21.92) otteniamo
H(Y ⁄ X) = ⎲⎳ip(xi)⎡⎢⎣ ⎲⎳jp(yj ⁄ xi)log21p(yj ⁄ xi)⎤⎥⎦ = Hb(pe)
dato che il termine tra parentesi quadre rappresenta appunto l’entropia di una sorgente binaria con simboli a probabilità
pe e
1 − pe. Possiamo quindi ora scrivere l’espressione cercata
che dipende sia dalla probabilità di errore
pe, sia dalla prob. a priori dei simboli della sorgente: osserviamo che se
pe≪1 il canale (quasi) non commette errori, e risulta
I(X, Y) ≃ Hb(α) = H(X), mentre se
pe → 12 allora
I(X, Y) → 0.