Rumore nei ripetitori: modalità trasparente e rigenerativa

Prev Sezione 18.2: Rumore nelle reti due porte Su Capitolo 18: Caratterizzazione circuitale, rumore ed equalizzazione dati Sezione 18.4: Equalizzazione numerica Next

18.3 Rumore nei ripetitori

Come illustreremo al cap. 19, la propagazione del segnale attraverso un mezzo trasmissivo ne determina una attenuazione la cui entità aumenta con la distanza. La realizzazione di un collegamento molto lungo mediante un’unica tratta è pertanto praticamente impossibile, sia a causa del livello troppo ridotto del segnale che sarebbe ricevuto, sia (per un collegamento radio) per la mancanza di condizioni di visibilità. Occorre pertanto suddividere il collegamento in più tratte, intervallate da stadi di amplificazione (o ripetitori) progettati in modo da compensare l’attenuazione del segmento appena attraversato.

18.3.1 Ripetitore trasparente

L’aggettivo trasparente si riferisce al fatto che, oltre al segnale, viene amplificato anche il rumore presente in ingresso, e nel caso di una trasmissione analogica, questo è l’unico modo di procedere. Le trasmissioni numeriche invece adottano un ripetitore rigenerativo che produce un nuovo segnale, privo di rumore ma con qualche bit errato in più: affronteremo questo caso al § 18.3.2.

Analizziamo ora la questione con riferimento ad un collegamento radio, anche se la trattazione può essere estesa ad altre tecniche trasmissive, come il cavo o le fibre ottiche, e consideriamo una successione di M tratte come mostrato in fig. 18.13. Il ripetitore (il triangolo) interposto tra ogni coppia di tratte (le saette) amplifica il segnale (ed il rumore) di una quantità pari al proprio guadagno disponibile G_{d_i}, reso uguale all’inverso dell’attenuazione disponibile della tratta precedente, ovvero G_{d_i} = ¹⁄_{A_{d_i}}. Il rumore termico accumulato alla fine del collegamento può essere calcolato con i metodi già discussi, ma considerando che il livello di segnale di uscita è lo stesso per tutti i ripetitori si ritrova il risultato ottenuto al § 8.4.1, come andiamo ad illustrare. Al § 18.3.1.2 valuteremo poi come le distorsioni di non linearità (§ 8.3) degli amplificatori possano intervenire nel progetto.

Figure 18.13 Suddivisione di un collegamento in M tratte, e relativo diagramma del livello di segnale in dB o ipsogramma

18.3.1.1 Rumore termico accumulato

In base all’uscita dell’ultimo ripetitore indicata come m(t) + n(t) si può definire un SNR complessivo come SNR_T = ^P_m⁄_{P_n}. D’altra parte il rumore n(t) è dovuto ai contributi di rumore n_i(t) introdotti nelle singole tratte; essendo tali contributi statisticamente indipendenti tra loro la potenza di rumore accumulata è la somma delle singole potenze:

P_n = σ²_n = E{n²(t)} = E⎧⎨⎩(⎲⎳_in_i(t))²⎫⎬⎭ = ⎲⎳_i E{n²_i(t)} = ^M⎲⎳_i = 1P_{n_i}

Deriviamo i singoli termini P_{n_i} osservando che all’uscita di ogni ripetitore è definito un SNR_i = ^P_{m_i}⁄_{P_{n_i}} locale da cui ottenere P_{n_i} = ^P_{m_i}⁄_{SNR_i}, consentendoci di scrivere

SNR_T = P_m∑^._i P_{n_i} = P_m∑^._i ^P_{m_i}⁄_{SNR_i}

A questo punto notiamo che, essendo il livello di segnale P_{m_i} in ingresso a ciascun ripetitore lo stesso, ovvero P_{m_i} = P_m per ∀i, i singoli contributi P_{n_i} al rumore complessivo possono essere espressi nei termini di uno stesso livello di segnale, ovvero P_{n_i} = P_mSNR_i, e dunque per l’SNR complessivo si ottiene

SNR_T = P_mP_m∑^._i 1SNR_i = 1∑^._i 1SNR_i

Questo risultato può essere espresso con la frase

l’SNR prodotto da più cause indipendenti è il parallelo degli SNR dovuti alle diverse cause di rumore

per via della analogia formale con l’espressione della resistenza equivalente di un parallelo di resistenze; l’analogia evidenzia, tra l’altro, che se una tratta è considerevolmente peggiore delle altre, SNR_T dipenderà essenzialmente da questa.

Il risultato a cui siamo giunti ha validità più generale del caso illustrato, e può essere invocato ogni volta che un sistema di comunicazione è affetto da più cause di disturbo additivo indipendenti tra loro, per ognuna delle quali si sia separatamente in grado di giungere ad una espressione di SNR, come illustrato anche al § 8.4.1.

Proseguiamo l’analisi ipotizzando ora che tutte le tratte siano uguali tra loro, ovvero con eguali A_d e G_d, uguali temperature di rumore, ed uguali SNR_i. In tal caso si ottiene

SNR_T = 1MSNR_i = SNR_iM

ovvero un M − esimo dell’SNR_i locale di ciascun ripetitore [1022] [1022] Con SNR_i = αSNR₀ = αP_RP_n, dove P_n = kT_{e_i}W è la potenza di rumore nella banda di messaggio W, P_R è la potenza ricevuta da un ripetitore (uguale per tutti se le tratte sono uguali), e α è un fattore che dipende dal tipo di modulazione (cap. 14).. Sembrerebbe dunque che per migliorare l’SNR complessivo sia sufficiente aumentare la potenza di trasmissione di tutti gli stadi, in modo da elevare la potenza ricevuta. In realtà la potenza trasmessa non può aumentare a piacere, in quanto intervengono fenomeni di non-linearità.

18.3.1.2 Compromesso tra rumore termico e distorsione

Ai §§ 8.3 e 13.3 si è studiato come per un segnale modulato la presenza di un elemento a comportamento non lineare (tipicamente l’amplificatore di potenza del ripetitore) produce interferenza in banda, la cui potenza P_NL dipende con legge cubica dalla potenza del segnale trasmesso. Indichiamo quindi con SNR_NL = P_mP_NL il rapporto SNR complessivo del collegamento dovuto a cause di non linearità, ed osserviamo che questo diminuisce all’aumentare della potenza trasmessa da ogni ripetitore. L’SNR complessivo deve tener conto sia del rumore termico che della distorsione non lineare, e dato che questi sono statisticamente indipendenti, può essere espresso come “il parallelo” di entrambi, ossia

SNR = 11SNR_T + 1SNR_NL

Dato che all’aumentare della potenza di trasmissione SNR_T diminuisce mentre SNR_NL aumenta, l’SNR complessivo presenta un massimo per un certo valore di potenza trasmessa, ovvero esiste un dimensionamento ottimo in grado di fornire il miglior SNR complessivo.

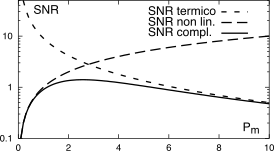
Esempio

La figura a lato mostra l’andamento di

SNR = 11SNR_T + 1SNR_I

dovuto ai due termini . SNR_T = P_m e SNR_NL = P_m.1 ⋅ P²_m + .01 ⋅ P³_m
Come si vede, con questi valori SNR presenta un massimo per P_m ≃ 2.5.

18.3.2 Ripetitore rigenerativo

Affrontiamo ora il caso in cui la trasmissione sia di natura numerica (§ 16): in tal caso i dispositivi intermedi di amplificazione anziché essere di tipo trasparente, vengono detti rigenerativi, ovvero mentre dal lato ricevente svolgono l’intero processo di decisione (§ 15.4) sui simboli del messaggio, dal lato di trasmissione generano un nuovo segnale in cui è assente il rumore presente in ricezione.

La valutazione delle prestazioni complessive nel caso si adottino M ripetitori

rigenerativi posti in serie lungo un medesimo collegamento è piuttosto semplice, qualora siano equispaziati, ed ognuno caratterizzato dalla stessa p = P^bit_e. In tale circostanza si ricade infatti nel caso delle prove ripetute, permettendo di esprimere la probabilità che lo stesso bit sia sbagliato da n ripetitori (su M) mediante la distribuzione di Bernoulli (§ 22.1) p(n) = ⎛⎝Mn⎞⎠pⁿ(1 − p)^M − n. Ovviamente il bit risulterà sbagliato solo se avrà subito un numero dispari di errori, e dunque complessivamente possiamo scrivere

P^T_e = ^M⎲⎳_{n = 1

n dispari}p(n) = Mp(1 − p)^M − 1 + M(M − 1)(M − 2)3!p³(1 − p)^M − 3 + ⋯

Nel caso, come spesso accade, che p ≪ 1, l’espressione indicata è bene approssimata dal solo primo termine, e dunque si può affermare che P^T_e ≃ MP^bit_e, ovvero che la prob. di errore sul bit è proporzionale al numero di tratte.

Esempio con un valore di p = 10^− 6 occorrono 10 tratte per arrivare a P^T_e = 10^− 5.

Ripetitore trasparente nelle trasmissioni numeriche

In questo caso ogni ripetitore trasparente amplifica oltre al segnale anche il rumore già presente, e ne aggiunge di suo: come mostrato al § 18.3.1.1 nel caso di tratte identiche all’estremo di destinazione del collegamento si osserva un SNR_T = SNR_iM, pari cioè a quello di ogni singola tratta, diviso per il numero delle tratte. In tal caso l’^E_b⁄_N₀ del ricevitore a destinazione (l’unico ora che esegue il processo di decisione) risulta ridotto dello stesso fattore M (vedi eq. (21.16) pag. 1), producendo un peggioramento delle sue condizioni operative di 10log₁₀M dB rispetto a quelle delle singole tratte.

Esercizio Una trasmissione numerica 16-qam (§ 16.3) è realizzata mediante un collegamento suddiviso in M = 16 tratte uguali. Qualora si desideri una P^T_e complessiva pari a 10^− 5, valutare il valore di ^E_b⁄_N₀ necessario in ingresso a ciascuna tratta, nei due casi a) ripetitori rigenerativi oppure b) ripetitori trasparenti. Indicare quindi l’entità del rapporto tra le potenze di segnale in ingresso ai ripetitori nei due casi.

Svolgimento Nel caso a) risulta P^T_e ≃ MP_e, dunque per ogni tratta si deve ottenere una P_e = ^{P^T_e}⁄_M = ^{10^− 5}⁄₁₆ = 6.25 ⋅ 10^− 7, a cui (per un 16-qam) corrisponde (fig. 16.22) un valore ^E_b⁄_N₀ ≃ 14.5 dB. Nel caso b) la decisione ha luogo solamente nell’ultima tratta, e per ottenere una P^T_e = 10^− 5, la modulazione 16-qam necessita di un valore ^E_b⁄_N₀ ≃ 13.5 dB. D’altra parte, per ottenere un tale ^E_b⁄_N₀ in ingresso al decisore, ogni tratta che lo precede deve presentare un ^E_b⁄_N₀ in ingresso allo stadio di amplificazione maggiore (rispetto a quello del decisore) di una quantità pari a log₂M = 4 dB, ossia ^E_b⁄_N₀ = 13.5 + 4 = 17.5 dB, ovvero 3 dB in più rispetto al caso a).
Essendo le tratte identiche per ognuna di esse il valore N₀ = ¹⁄₂kT_ei è lo stesso, in quanto (vedi eq. 21.133) T_ei = T_g + T₀(F − 1), e sia T_g che F sono gli stessi per tutte le tratte. Pertanto la differenza di 3 dB tra i valori di ^E_b⁄_N₀ nei casi a) e b) si riflette in un raddoppio della potenza in ingresso ad ogni ripetitore trasparente, in confronto a quello rigenerativo.

Prev Sezione 18.2: Rumore nelle reti due porte Su Capitolo 18: Caratterizzazione circuitale, rumore ed equalizzazione dati Sezione 18.4: Equalizzazione numerica Next