24.8 Commutazione
Illustriamo ora l’architettura dei dispositivi che consentono la cosiddetta
commutazione di circuito, ovvero la creazione di un collegamento
stabile tra due porte del commutatore, con un
impegno permanente di
risorse fisiche per tutta la durata del collegamento. L’altra modalità di commutazione, quella di
pacchetto, è stata illustrata al cap.
22.
24.8.1 Reti a divisione di spazio
Individuano gli organi di commutazione che realizzano un collegamento fisico (elettrico) tra uno degli
N ingressi ed una delle
M uscite. Nel caso in cui
N > M, la rete è un
concentratore, mentre se
N < M la rete è un espansore; se
N = M la rete è quadrata e
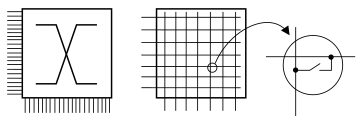
non bloccante. Il commutatore è rappresentato da un blocco con una “X” (in inglese
cross, od incrocio), e può essere pensato come una matrice binaria in cui ogni elemento (1 o 0) rappresenta lo stato (chiuso od aperto) di un interruttore (realizzato ad esempio mediante un transistor) che collega una linea di ingresso ad una di uscita.
Realizzare in questo modo una rete non bloccante prevede l’uso di un numero di interruttori pari ad N ⋅ M, dei quali solo min(N, M) sono utilizzati, anche nelle condizioni di massimo carico. Inoltre, nessun interruttore può essere “eliminato” senza precludere irrimediabilmente la possibilità di collegare qualunque ingresso a qualunque uscita. Allo scopo di utilizzare un numero ridotto di interruttori, sia per costruire reti non bloccanti oppure bloccanti con bassa probabilità di blocco, si ricorre alle...
24.8.2 Reti multistadio
...di cui alla figura
24.30 è riportato un esempio a 3 stadi, con gli
N ingressi che sono ripartiti su
r1 reti più piccole con
n ingressi, e le
M uscite su
r3 reti con
m uscite. Nel mezzo ci sono
r2 reti con
r1 ingressi ed
r3 uscite. Si può dimostrare che la rete complessiva è
non bloccante se il numero di matrici dello stadio intermedio è almeno
r2 ≥ n + m − 1 (condizione di
clos). Una connessione da sinistra a destra ha ora la
possibilità di scegliere attraverso quale matrice intermedia passare.
Nel caso di reti quadrate (N = M), ponendo n = m = √N2, si ottiene un numero complessivo di incroci pari a 4(√2 N32 − N), che risulta inferiore ad N2 (e dunque vantaggioso rispetto ad un commutatore monostadio) a partire da N ≥ 24.
Ovviamente, la problematica relativa alle matrici di commutazione è molto articolata, coinvolgendo topologie più complesse, filosofie di instradamento, e tecniche per la stima delle probabilità di blocco. Tralasciamo ulteriori approfondimenti, per illustrare invece come realizzare dispositivi di commutazione per trasmissioni numeriche a divisione di tempo.
24.8.3 Commutazione numerica a divisione di tempo
Consideriamo il caso in cui si debbano commutare le comunicazioni associate ai singoli
time-slot presenti in diversi flussi numerici organizzati in trame. Avendo a disposizione solamente una matrice di commutazione spaziale, quest’ultima può essere
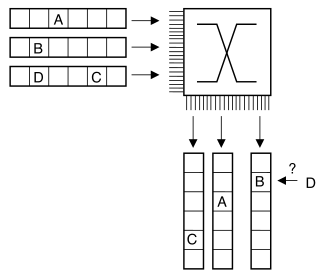
riprogrammata alla stessa frequenza dei time-slot, consentendo alle comunicazioni entranti di dirigersi verso i flussi uscenti in direzione delle rispettive destinazioni finali. La matrice spaziale, però, non può alterare l’ordine temporale dei dati in ingresso! Come rappresentato nella figura a lato, non può (ad esempio) inviare le conversazioni
B e
D sulla stessa linea uscente, in quanto si verifica un conflitto temporale. E’ quindi evidente la necessità di introdurre uno stadio di
commutazione temporale.
24.8.3.1 Time Slot Interchanger
Questo dispositivo è indicato come
tsi (Time Slot Interchanger) ed ha la funzione di produrre in uscita una sequenza di dati identica a quella in ingresso, tranne per
averne cambiato l’ordine temporale. In figura è mostrato un possibile schema di funzionamento: una trama entrante viene scritta, agli indirizzi ottenuti leggendo sequenzialmente la tabella di scambio, in un buffer di memoria (
es.: entra E
e lo scrivo al 4o posto, poi entra D
e va al 1o posto, etc.). Prima dell’inizio di una nuova trama, il primo buffer è copiato in un secondo, che a sua volta viene letto con ordine sequenziale (partendo dall’alto), per creare la nuova trama in uscita. Ovviamente, è possibile anche la realizzazione opposta, con scrittura sequenziale e lettura secondo il nuovo ordinamento.
24.8.3.2 Commutazione bidimensionale
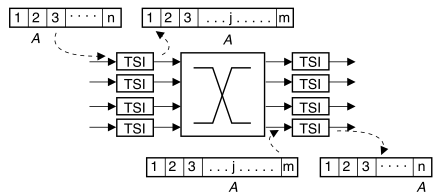
Così come un commutatore spaziale non è sufficiente, anche un tsi “da solo” è di scarsa utilità, non potendo instradare le comunicazioni su vie diverse. Combinando assieme le due funzioni si riescono a realizzare commutatori sia di tempo che di spazio, come la struttura a 3 stadi in figura, chiamata “tst” perché alterna uno stadio temporale, uno spaziale ed uno temporale.
Notiamo subito come in questo schema il numero di intervalli temporali
in uscita dai
tsi di ingresso è maggiore di quelli
in ingresso ossia
m > n (): ciò determina, per lo stadio spaziale, una frequenza di commutazione più elevata della frequenza dei time-slot in ingresso. Una generica conversazione “A” che occupa il
2o slot del primo flusso può raggiungere (ad esempio) l’ultimo slot dell’ultimo flusso, occupando uno qualsiasi (
j) degli
m slot utilizzati dal commutatore spaziale. Aumentando il valore di
m, si riduce la probabilità di blocco; in particolare, questa è nulla se
m = 2n − 1().
Analizziamo i vantaggi conseguiti dalla commutazione numerica con un semplice esempio. Poniamo di voler commutare con lo schema illustrato 4 flussi pcm (con n = 30): i 4 * 30 = 120 canali presenti sono commutati utilizzando solo 4 * 4 = 16 interruttori, contro i 120 * 120 = 14.400 interruttori necessari ad una matrice spaziale monostadio che svolga la commutazione dei 120 canali analogici !