13.3 Distorsione non lineare per segnali modulati
Già al §
8.3 si è analizzato il fenomeno della distorsione
di non linearità, focalizzando l’attenzione sui segnali di banda base, e sulla generazione di componenti spettrali a frequenze assenti dal segnale di ingresso, eliminabili mediante filtraggio. Nel caso di segnali modulati una non linearità produce conseguenze peculiari, affrontate in questa sede.
13.3.1 Limitazione di potenza per modulazione AM
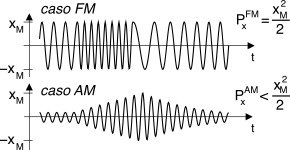
Una delle prime conseguenze della non linearità degli apparati sui segnali modulati differenzia i casi
fm ed
am per quanto riguarda la massima potenza a cui è possibile trasmettere. Nel primo caso infatti il segnale mantiene sempre la stessa ampiezza, che può essere posta pari a
xM ossia al massimo valore di ingresso al dispositivo non lineare (tipicamente, un amplificatore) prima che inizi a manifestarsi il fenomeno della sataurazione (vedi fig. a pag.
1). Pertanto la potenza del segnale trasmesso è pari a
P FMx = x2M⁄2, condizione detta anche di
piena potenza.
Al contrario, nel caso della trasmissione di un segnale
am l’inviluppo di ampiezza del segnale è fortemente variabile nel tempo: per evitare di operare in regione non lineare, questa volta
xM è il valore
massimo dell’inviluppo di ampiezza, e la potenza di trasmissione del segnale deve essere minore di quella
piena, una sorta di
arretramento indicato anche come
back-off. Pertanto a differenza del caso
fm, la trasmissione
am deve operare con una potenza
PAMx < PFMx minore della massima consentita dall’amplificatore, mentre per trasmettere la stessa potenza è necessario ricorrere ad un amplificatore sovradimensionato.
13.3.2 Distorsione di terza armonica
Riprendiamo il discorso iniziato al §
8.3.2, in cui si è analizzato l’effetto di una non linearità su di un processo gaussiano stazionario a media nulla, con potenza
Px e densità spettrale
Px(f), giungendo a dimostrare la comparsa dei termini di secondo e terzo ordine
PII(f) e
PIII(f) espressi come
Dato che ora il processo è un segnale modulato con portante
f0, eseguendo la costruzione grafica (§
3.4.3) per le convoluzioni presenti nella
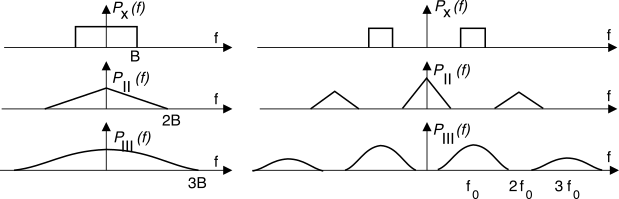
(14.84) osserviamo (fig.
13.14) che il termine
PII(f) occupa regioni di frequenza (con banda doppia rispetto a
Px(f)) centrate ad
f = 0 e
f = 2f0, disgiunte dalla banda di
Px(f): pertanto
PII(f) può
essere non considerato fonte di disturbo - se non a danno di eventuali altre trasmissioni a frequenza
2f0.
Infine, la convoluzione tra
PI(f) e
PII(f) fornisce una
PIII(f) costituita anch’essa da due componenti, di cui una centrata ad
f = 3f0 e che, come per
PII(f), non produce disturbo se non ad altre trasmissioni; mentre una parte più consistente di
PIII(f) è centrata sulla stessa portante
f0 di
x(t), e dunque costituisce effettivamente fonte di disturbo, come si dice,
in banda. In definitiva, vi sono almeno tre buone ragioni per
tenere d’occhio il valore di
β (vedi
(10.209) per la sua definizione), che è causa delle distorsioni
di terza armonica:
- è il coefficiente che tiene conto dei fenomeni di saturazione;
- produce interferenza in banda per i segnali modulati;
- produce interferenza fuori banda che danneggia le trasmissioni a frequenza tripla.
13.3.3 Insensibilità della modulazione angolare alle non linearità
Di nuovo, la modulazione
fm si dimostra più tollerante della
am rispetto alle non-linearità, al punto che la distorsione
in banda discussa al § precedente si dimostra
non essere un disturbo. Infatti, applicando la notazione introdotta con
(10.209) ad un segnale modulato angolarmente, ovvero del tipo
x(t) = cos[ω0t + φ(t)], l’attraversamento di un dispositivo con caratteristica ingresso-uscita approssimata come
y(t) = x(t) + αx2(t) + βx3(t) produce una uscita (vedi eq.
(10.210))
y(t) = α2 a2(t) + ⎛⎝1 + 34 β⎞⎠ cos[ω0t + φ(t)] + α2 cos[2ω0t + 2φ(t)] + β4 cos[3ω0t + 3φ(t)]
Dopo che i termini a frequenza
2ω0 e
3ω0, nonché la costante additiva, sono eliminati mediante un filtro passa-banda centrato in
f = f0 = ω02π, rimane solamente il termine
z(t) = ⎛⎝1 + 34β⎞⎠ cos[ω0t + φ(t)]. Pertanto, la modulazione di fase
φ(t) è esattamente la stessa di quella impressa dal modulatore, e quindi i fenomeni non lineari
non hanno conseguenze sulla modulazione angolare! Tranne, ovviamente, che per le interferenze causate alle trasmissioni su portanti a frequenza doppia e tripla di
fo.
L’insensibilità dei segnali modulati angolarmente nei riguardi delle non linearità è stata ad esempio sfruttata nei collegamenti in ponte radio progettati per trasmettere un segnale FDM in modulazione di frequenza (§
11.1.1.2), adottando un basso indice di modulazione (risparmiando banda) e trasmettendo a piena potenza (vedi §
8.3). In questo modo, la potenza del segnale trasmesso
non dipende dal numero di canali contemporaneamente attivi.
13.3.4 Predistorsione
A differenza dei segnali modulati angolarmente, quelli a modulazione di ampiezza - qualora non limitati in potenza come descritto al §
13.3.1 - subiscono pienamente l’effetto di distorsione non lineare, che si ripercuote sulla ampiezza della portante, ed in egual misura sul segnale demodulato.
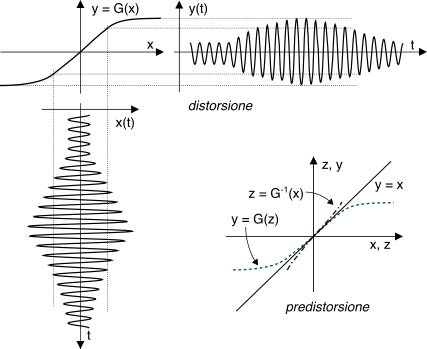
Nel caso in cui i parametri che caratterizzano la non-linearità
y = G(x) siano noti, un rimedio che viene tentato è quello di far passare il segnale modulato (prima della sua trasmissione) attraverso un nuovo elemento non lineare appositamente realizzato in modo che effettui una trasformazione
inversa ovvero
z = G− 1(x) con
G− 1 tale che
G(z) = G(G− 1(x)) = x
fornendo quindi in ingresso all’elemento non lineare
G il segnale
predistorto z = G− 1(x) anziché quello originale
x, neutralizzando così il fenomeno di non linearità.