8.3 Distorsione da non linearità
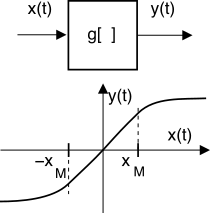
Si tratta di un fenomeno che non dipende da un effetto memoria o dalla frequenza, come avviene nel caso della distorsione lineare. Al contrario, quella non lineare consiste nell’effetto prodotto su di un segnale dall’attraversamento di un dispositivo la cui caratteristica ingresso-uscita istantanea descrive un comportamento non lineare, per il quale cioè la relazione ingresso-uscita è del generico tipo y(t) = g[x(t)] ≠ ax(t) + b, ovvero ogni valore di uscita dipende unicamente da quello di ingresso al medesimo istante, secondo una relazione appunto non lineare.
Un tipico caso di distorsione non lineare si verifica quando un amplificatore è alimentato da un segnale di ingresso con dinamica troppo elevata.
Indicando con
xM il massimo valore di ingresso per cui l’amplificatore mantiene un comportamento lineare, valori di
|x(t)| > xM provocano il fenomeno della
saturazione, caratterizzato dalla curva ingresso-uscita dalla forma
ad s mostrata in figura.
Comparsa di nuove frequenze
E’ forse la conseguenza più appariscente della distorsione di non linearità. Prima di addentrarci in un modello analitico del fenomeno, può essere istruttivo riflettere sul risultato sperimentale mostrato in fig.
8.10.
Un segnale sinusoidale a frequenza 5 Hz viene campionato con
fc = 100 Hz ottenendo 256 campioni di cui si valuta la densità di energia tramite
dft, con l’esito mostrato su di una scala in dB alla prima colonna, riproducendo in pratica la situazione di fig.
4.25, compreso l’effetto della finestra rettangolare. Lo stesso segnale viene quindi fatto passare attraverso una non linearità del tipo di quella mostrata sopra, causando la lieve distorsione della forma d’onda mostrata al centro di fig.
8.10: osserviamo in tal caso la comparsa di una componente a frequenza tripla, seppure con energia di 30 dB (pari a un millesimo) inferiore. L’ultima colonna mostra infine il risultato di una saturazione
più ripida, al punto che la forma d’onda diviene quasi squadrata, producendo un numero più elevato (e più intenso) di armoniche, sempre dispari. In definitiva, sappiamo già (§
2.2.2) che un’onda quadra ha solo armoniche dispari!
Dato che in presenza di fenomeni non lineari decade il principio di sovrapposizione degli effetti, per descrivere il fenomeno in forma analitica si procede studiando prima il caso di un semplice segnale sinusoidale, e quindi si accenna ai risultati ottenibili per processi gaussiani. In entrambi i casi, l’analisi si basa sullo sviluppo di
g[x(t)] in serie di potenze arrestato al terzo ordine, in modo da poter scrivere
in cui
G = dg dx||x = 0 rappresenta il guadagno dell’amplificatore, ed i coefficienti
α = 12G d2g dx2||x = 0 e β = 1 6G d3g dx3||x = 0
tengono conto degli effetti di secondo e terzo ordine. Notiamo anche come il termine legato a β sia quello che tiene conto dell’effetto della saturazione, in virtù della simmetria dispari di x3.
8.3.1 Ingresso sinusoidale
Ponendo
x(t) = Acosω0t la
(10.209) si riscrive come
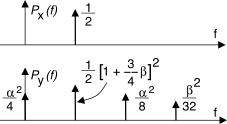
Ricordando ora che la potenza di una cosinusoide di ampiezza
A è pari ad
A2 2, alla
(10.210) corrisponde lo spettro di densità di potenza disegnato a lato, detta
spettro unilatero in quanto non tiene conto delle frequenze negative, ed ottenuto per
A = G = 1: osserviamo chiaramente sia la comparsa di termini a frequenza doppia e tripla di quella di ingresso, sia di una componente continua.
In molti casi l’esatta relazione
y(t) = g[x(t)] non è però nota, e dunque non lo sono i coefficienti
α e
β. Il loro valore viene quindi ottenuto per via
sperimentale ponendo in ingresso una sinusoide di potenza nota, osservando la potenza delle armoniche presenti in uscita, e sfruttando la relazione
(10.210) come descritto appresso.
Fattori di intermodulazione
Le caratteristiche tecniche che accompagnano gli amplificatori riportano, invece di
α e
β, i valori dei
fattori di intermodulazione μ2 e
μ3 (detti di seconda e di terza armonica), ottenuti per via sperimentale utilizzando un ingresso
sinusoidale, misurando le potenze in uscita
PI,
PII e
PIII oltre che alla frequenza in ingresso anche alla sua seconda e terza armonica, e definendo in base ai loro rapporti le quantità
da cui si possono ottenere i coefficienti
α e
β mediante le relazioni
α ≃ 1.41 ⋅ μ2 ⋅ G e
β = 2 ⋅ μ3 ⋅ G2, come calcolato alla nota.
Dato che dalle
(10.211) possiamo scrivere
PII = μ22 ⋅ P2I e
PIII = μ23 ⋅ P3I, osserviamo che per piccoli valori di
PI la distorsione prodotta sia da
PII che da
PIII è trascurabile; all’aumentare di
PI,
PII cresce con il quadrato della potenza della sinusoide in ingresso, mentre
PIII con il cubo, e dunque la potenza della terza armonica
PIII finisce per divenire predominante.
Con alcuni passaggi trigonometrici si può infine mostrare che qualora il segnale in ingresso contenga più di una sinusoide, in uscita saranno presenti anche termini a frequenza pari alla somma ed alla differenza di ogni coppia di frequenze in ingresso, oltre a tutti i loro multipli: tale fenomeno viene indicato come distorsione di intermodulazione.
8.3.2 Ingresso aleatorio
Per sviluppare l’analisi dell’effetto che la distorsione non lineare produce su di un segnale a spettro continuo ci poniamo in un’altra situazione-limite, studiando il caso in cui l’ingresso
x(t) sia membro di un processo gaussiano stazionario a media nulla, con potenza
Px e densità spettrale
Px(f).
Al §
8.5.1 vengono discussi i passaggi che, in virtù di alcune proprietà dei momenti di variabili aleatorie gaussiane, consentono di giungere ad una espressione della densità spettrale
Py(f) del processo
y(t) = G[x(t) + αx2(t) + βx3(t)] in uscita dalla non linearità nei termini della trasformata di Fourier della relativa funzione di autocorrelazione
Ry(τ). Il risultato mostra che oltre ad un termine in continua e ad una amplificazione di
Px(f), in uscita si manifestano anche i due termini additivi
PII(f) = G22α2 ⋅ Px(f) * Px(f); PIII(f) = G26β2 ⋅ Px(f) * Px(f) * Px(f)
che rappresentano
l’effetto distorcente della non linearità: notiamo che per entrambi i contributi si verifica una
convoluzione in frequenza della
Px(f) originaria
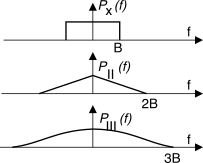
con se stessa. Nel caso di un segnale
x(t) di banda base i termini
PII(f) e
PIII(f) dovuti alla non linearità occupano pertanto una banda di estensione rispettivamente doppia e tripla di quella di
Px(f) come per il caso di esempio mostrato in figura, in cui una
Px(f) rettangolare convoluta con se stessa ne produce una triangolare di base doppia, o più smussata quando convoluta tre volte. Pertanto, solo una parte della potenza totale del segnale di errore dovuto alla distorsione giace nella stessa banda di segnale. Il caso relativo ad un segnale
x(t) modulato viene invece trattato al §
13.3.