12.4 Appendici
12.4.1 Mixer mediante non linearità
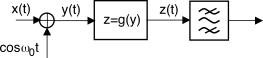
Illustriamo un modo di realizzare il dispositivo che effettua la funzione di moltiplicazione tra un segnale modulante ed una portante. Sebbene esistano schemi circuitali capaci di realizzare esattamente il prodotto tra due segnali analogici, l’approccio che segue è molto semplice, e fa uso di un sommatore, un oscillatore, un dispositivo non lineare, ed un filtro passa-banda, come mostrato in figura.
Il dispositivo non lineare ha una caratteristica ingresso-uscita del tipo
z = a1y + a2y2 + a3y3 + ⋯
e quando in ingresso viene applicata la somma di due segnali
x(t) + cosω0t, produce
z(t) = a1(x(t) + cosω0t) + a2(x2(t) + cos2ω0t + 2x(t)cosω0t) + a3(⋯) + …
da cui, osservando che i termini
cosnω0t sono relativi a componenti centrate a frequenza
nf0, il filtro passa banda può estrarre il termine
x(t)cosω0t a cui siamo interessati.
Da un punto di vista circuitale il dispositivo non lineare può essere costituito da un semplice diodo, per il quale la corrente che lo attraversa è espressa in funzione della tensione V ai suoi capi in base all’espressione I = Is(eV⁄α − 1) in cui Is ed α sono delle costanti; per piccoli valori di V la relativa espansione in serie di Taylor permette infatti di scrivere eV⁄α − 1 ≃ V⁄α + (V⁄α)22 e dunque, ponendo V = x(t) + cosω0t si ottiene il risultato anticipato.
12.4.2 Mixer a commutazione
Non è strettamente necessario disporre di un oscillatore sinusoidale per realizzare il prodotto di un segnale con una portante: è sufficiente un’onda quadra ed un filtro! Infatti, un qualunque segnale periodico
y(t) = g(t) *∞⎲⎳n = −∞δ(t − nT)
di periodo
T = k ⁄ f0 (con
k intero) possiede una densità di potenza
Il prodotto di tale segnale per
x(t) produce un segnale
z(t) con densità di potenza
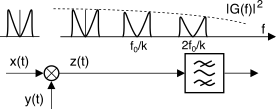
Pertanto, il desiderato spettro di potenza si ottiene inserendo dopo il moltiplicatore un filtro passa banda centrato su una delle armoniche a frequenza
nk f0 di
y(t), ovvero su una delle repliche spettrali che compongono
Pz(f). L’inviluppo mostrato in figura è relativo ad una scelta per
g(t) del tipo
g(t) = rectτ(t) con
τ sufficientemente minore di
k ⁄ f0 e scelto in modo opportuno, in modo che se la banda di
x(t) è sufficientemente ridotta rispetto a
f0 ⁄ k l’entità della distorsione lineare di ampiezza può essere considerata trascurabile. Lo stesso dispositivo può essere usato anche per i moltiplicatori di demodulazione: in tal caso, il filtro da usare sarà un passa basso.
Dato che un punto vista circuitale il prodotto per un’onda quadra è assimilabile ad un interruttore che si apre e si chiude, un dispositivo del genere viene detto switching mixer.
12.4.3 Sintesi di frequenza con PLL ed oscillatore a cristallo
Questa sottosezione illustra una tecnica per generare una portante di modulazione (oppure eterodina) che sia
stabile in frequenza. Dato che tutti questi elementi sono ormai integrati in un unico
chip, possiamo anche visitare quelli a catalogo di un produttore
a caso! Essenzialmente il circuito
pll illustrato al §
12.2.2.2 non è in grado di generare una portante
di modulazione stabile a sufficienza, in quanto ottenuta a partire da oscillatori realizzati mediante circuiti di tipo analogico, la cui frequenza dipende anche dalla precisione dei valori dei componenti utilizzati e dalla temperatura di lavoro, oltre a presentare una variabilità che aumenta al crescere della frequenza di oscillazione. Al contrario, gli oscillatori basati su di un cristallo sono molto più stabili e precisi, tipicamente dell’ordine di
±20 ppm, anche se il loro costo, disponibilità e fragilità peggiora all’aumentare della frequenza, arrivando in pratica a qualche decina di MHz.
Per generare portanti più elevate si utilizza la frequenza dell’oscillatore a cristallo come un
riferimento a cui far
agganciare un circuito
pll modificato come in figura
12.33,
in cui le forme d’onda sono di tipo rettangolare in modo da poterne ottenere
di nuove con periodo multiplo di quello di partenza (e dunque frequenza pari ad un suo sottomultiplo) mediante l’uso di un circuito divisore
modulo
N. In particolare, il moltiplicatore è ora detto
comparatore di fase ed opera (per forme d’onda bipolari) come mostrato nella parte inferiore di fig.
12.33, producendo un’onda bipolare a
valor medio positivo o negativo a seconda se l’ingresso a sinistra sia in anticipo od in ritardo rispetto a quello proveniente dal basso, valor medio che è proporzionale allo slittamento in eccesso rispetto alla condizione di uno sfasamento pari ad un quarto di periodo.
La frequenza f0 generata dal vco si aggancia quindi ad un valore N volte maggiore di quello fd in ingresso al comparatore, in virtù del divisore per N posto a valle del vco; essendo il divisore di tipo programmabile, la frequenza del segnale prodotto dal vco può essere modificata variando il valore di N. Allo stesso tempo, anche la frequenza fc prodotta dall’oscillatore a cristallo viene divisa per un diverso numero M, in modo che la frequenza di uscita risulti pari a f0 = NM fc. In tal modo il circuito può essere programmato per generare frequenze NM volte maggiori di quella prodotta dal cristallo, mantenendo la sua stessa precisione: ad esempio un cristallo con precisione di 20 ppm e frequenza fc = 10 MHz, dopo aver scelto M = 1 ed N = 20, permette di ottenere f0 = 200 MHz ±4 KHz.
Moltiplicatore di frequenza
Il medesimo schema può essere impiegato per produrre più segnali di clock tutti multipli di una comune velocità di partenza, ad esempio nell’ambito di reti logiche complesse, o all’interno di microprocessori.
12.4.3.1 Sintesi digitale diretta
Si tratta della possibilità di generare le portanti di modulazione e demodulazione per via completamente numerica, nella forma di una sequenza costituita da valori dei campioni della forma d’onda sinusoidale letti da una memoria che viene indirizzata da un contatore ciclico. L’argomento sarà approfondito in una prossima edizione.
12.4.4 Densità di potenza per segnali AM a banda laterale unica
Affrontiamo il problema di dimostrare che per un segnale
am-blu a banda laterale
superiore (§
12.1.2) si ottiene
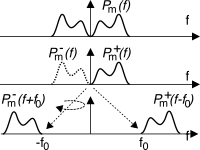
Px(f) = Pm+(f − f0) + Pm−(f + f0)
come asserito all’eq.
(14.45). A tale proposito osserviamo che la
(14.20) stabilisce
in cui
Px(f) = F {Rx(τ)}, e dato che nel nostro caso
x(t) = m(t) + j^m(t) = 2m+(t) (vedi eq.
(14.17)), otteniamo
in cui si è fatto uso della notazione di prodotto scalare
⟨ . , . ⟩ per generalizzare il calcolo dell’autocorrelazione sia al caso di segnale di potenza, sia a quello di un processo. Eseguendo ora la trasformata di
(14.60) otteniamo
Px(f) = 4 Pm+(f) = 4 Pm(f)|Hfp(f)|2
in cui
Hfp(f) è definito al §
11.2.6, e pertanto
Px(f) esiste solamente sul semiasse
delle frequenze positive. Dunque la
(14.59) si riscrive considerando che per
f > 0 si ha
Px(f)|f > 0 = 14 Px(f − f0) = Pm+(f − f0)
mentre per
f < 0 risulta
Px(f)|f < 0 = Pm+( − f − f0) = Pm−(f + f0)
come mostrato in figura.
12.4.5 Calcolo della potenza di un segnale AM BLU
Come anticipato in fondo al §
12.1.2, mostriamo che se
allora
Px = k2a2 Pm. Possiamo innanzitutto scrivere che
in quanto le componenti a frequenza positiva e negativa di
x(t) sono ortogonali, e lo spettro di densità di potenza è una funzione pari della frequenza:
Px(f) = Px(−f). Inoltre, invertendo la relazione
Px(f) = 4 Px+(f + f0) valida per la densità di potenza dell’inviluppo complesso, otteniamo
Px+(f) = 14 Px(f − f0), e quindi
Px+ = 14∞⌠⌡ −∞Px(f − f0)df = 14 Px
che, sostituita nella
(14.62), fornisce
Px = 2 Px+ = 12 Px.
Come sappiamo
Px = Rx(0) in cui, nell’ipotesi di processo ergodico,
Rx(0) è l’autocorrelazione di un qualunque membro, ad es. proprio di
(14.61), e dunque essendo in tal caso
x(t) = ka√2 [m(t) + j^m(t)], si ottiene
Px = 12 Px = 12Rx(0) = 12 ⎛⎝ka√2⎞⎠2 [Rmm(0) + R^m^m(0) + 2jRm^m(0)]
Osserviamo ora che
Rm^m(0) = ∫∞−∞m(t)^m(t)dt = 0 in quanto
m(t) ed
^m(t) sono ortogonali; inoltre,
Rmm(0) = Pm = R^m^m(0) (non dimostrato). Pertanto si ottiene
Px = 12 k2a2 [ Pm + Pm] = 14 k2a ⋅ 2 Pm = k2a2 Pm
12.4.5.1 Calcolo della potenza di segnali BLD-PI, PS, PPS
La tabella al §
12.1.4 è calcolata adottando lo stesso procedimento sopra esposto al §
12.4.5, in cui ora
Px = Pxc = ⎧⎨⎩ k2aPm (bld-ps) a2p + k2aPm (bld-pi, bld-pps)
12.4.6 Modulazione FM a basso indice
Riprendiamo qui il caso in cui
β≪1 e di conseguenza
Δα≪1, consentendo quindi di arrestare al 1° ordine lo sviluppo in serie di potenze (eq.
(14.52)) di
x(t). Se il segnale modulante è cosinusoidale, il segnale FM risulta
xFM(t) = a cos(ω0t + 2πkft⌠⌡ −∞cos(2πwτ)dτ) = a cos(ω0t + β sin(2πwτ))
Ricordando che
cos(α + β) = cosα cosβ − sinα sinβ,
xFM(t) può essere riscritto come
xFM(t) = a cos ω0t cos (βsin2πwt) − a sin ω0t sin (βsin2πwt)
che, se
β ≪ 1, diviene
che confrontiamo con l’espressione
che si otterrebbe per modulazione a portante intera, o ridotta, dello stesso
m(t).
Il confronto tra
(14.63) e
(14.64) rivela che mentre nell’
am il segnale modulante moltiplica una portante
in fase a quella (più o meno) intera, nell’
fm a basso indice
m(t)
opera su di una portante in
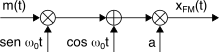
quadratura. Questa considerazione è alla base dello
schema di modulazione per segnali
fm a basso indice mostrato a lato e realizzabile
sommando alla portante un segnale
am-bld, modulato su di una portante in quadratura.
D’altra parte, uno schema di modulazione del genere produce anche una modulazione
am parassita: questa può essere eliminata in ricezione dall’azione congiunta di uno squadratore e di un filtro passa basso, come discusso in fondo al §
12.3.2.2.