Teorema di Wiener e densità di potenza di processo armonico, gaussiano, segnale dati

Prev Sezione 7.1: Correlazione, covarianza e autocorrelazione Su Capitolo 7: Correlazione, densità spettrale e filtraggio Sezione 7.3: Stima spettrale Next

7.2 Spettro di densità di potenza

Siamo finalmente in grado di caratterizzare questa densità spettrale sia per il caso dei processi che per gli altri tipi di segnale, di potenza, periodico, o di energia. Lo strumento che lo consente è il...

7.2.1 Teorema di Wiener

Si enuncia senza troppe complicazioni [363] [363] In realtà le attribuzioni di questo risultato sono molteplici, comprendendo anche Khinchin, Einstein e Kolmogorov - fonte https://it.wikipedia.org/wiki/Teorema_di_Wiener-Khinchin:

Lo spettro di densità di potenza P_x(f) (o di energia E_x(f)) di un segnale x(t) certo o aleatorio è pari alla trasformata di Fourier della relativa funzione di autocorrelazione, ovvero P_x(f) = F {R_x(τ)}

La dimostrazione del teorema per segnali di energia è straordinariamente semplice:

R_x(τ) = ⌠⌡^∞_−∞ x^*(t)x(t + τ)dt = ⌠⌡^∞_−∞ X^*(f)X(f) e^j2πfτdf = = F ⁻¹{X^*(f)X(f)} = F ⁻¹{E_x(f)}

in cui abbiamo prima applicato il teorema di Parseval (pag. 1), poi la proprietà di traslazione nel tempo, e quindi (vedi § 3.2) riconosciuta X^*(f)X(f) come la densità di energia E_x(f).

Come anticipato, il teorema è valido anche per segnali di potenza, per i quali la funzione di autocorrelazione R_x(τ) da cui partire è quella espressa dalla (10.154) ( [364] [364] In tal caso una stima della densità di potenza può essere ottenuta mediante periodogramma (§ 7.3.1) calcolato su di un segmento di segnale x_T(t) di durata T estratto da x(t), e facendo tendere T → ∞, ovvero P_x(f) = lim_{T → ∞}1 T |X_T(f)|². Dato che |X_T(f)|² è proprio la densità di energia E_{x_T}(f) di x_T(t), per il teorema di Wiener la sua anti-trasformata corrisponde alla funzione di autocorrelazione R_{x_T}(τ) = F ⁻¹{E_{x_T}(f)} di x_T(t), come definita dalla (10.155). Operando il passaggio al limite, si ottiene che

F ⁻¹{P_x(f)} = F ⁻¹lim_{T → ∞}{1 T |X_T(f)|²} = F ⁻¹⎧⎨⎩lim_{T → ∞} 1 T E_{x_T}(f)⎫⎬⎭ = lim_{T → ∞} 1 T R_{x_T}(τ)

corrispondente alla autocorrelazione R_x(τ) dell’intero segnale, come espressa dalla (10.154).

). Nel caso di processi ergodici, ogni membro del processo possiede la stessa P_x(f), che dunque può essere calcolata a partire dalla R_x(τ) di uno qualunque di essi. Nel caso di processi stazionari almeno in senso lato, infine, l’autocorrelazione da cui partire [365] [365] La dimostrazione del caso dei processi viene svolta al § 7.7.3; la sua validità è vincolata a processi per i quali ∫|τ ⋅ m^(1, 1)_XX(τ)|dτ < ∞, ed è basata sulla considerazione che se la P^θ_x(f) di un particolare membro θ è valutabile come P^θ_x(f) = lim_{T → ∞}1 T |X^θ_T(f)|², allora la sua media di insieme può scriversi come P_x(f) = lim_{T → ∞} 1 T E_Θ{|X^θ_T(f)|²}. è il momento misto m^(1, 1)_XX(τ) = E{x(t)x(t + τ)} calcolato come media di insieme dalla (10.153), e rappresenta il modo più generale di procedere, come applicato al § 7.7.4 per il caso di un segnale dati.

Discussione

Il teorema di Wiener è (nella sua semplicità) uno strumento molto potente che può costituire una strada alternativa per verificare ed estendere risultati noti. Ad esempio, la proprietà di massimo nell’origine per l’autocorrelazione R_x(0) = P_x può ora essere ricavata da quella del valore iniziale eq. (10.38):

R_x(0) = F ⁻¹{P_x(f)}|_τ = 0 = ^∞⌠⌡_−∞ P_x(f)e^j2πfτdf|_τ = 0 = ^∞⌠⌡_−∞ P_x(f)df = P_x

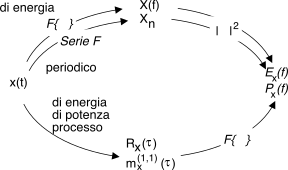
D’altra parte, la validità del teorema anche per segnali periodici e di energia consente di intraprendere per essi due percorsi alternativi per il calcolo delle corrispondenti P_x(f) e E_x(f), come illustrato nella figura a lato.

Dato che in virtù del teorema di Wiener è ora possibile definire una P_x(f) anche per processi e segnali di potenza, molto spesso nel testo ci si riferirà alle densità di potenza o di energia anziché alle trasformate dei segnali, in modo da applicare i risultati a tutti i casi possibili.

Applichiamo ora ad alcuni casi notevoli di segnale certo e processo aleatorio la relazione tra P_x(f) e R_x(τ) espressa dal teorema di Wiener.

7.2.2 Segnale periodico

In questo caso x(t) con periodo T può essere espresso mediante la relativa serie di Fourier (10.7) x(t) = ∑^∞_{n = −∞}X_n e^j2πnFt riferita alla frequenza fondamentale F = ¹⁄_T (o prima armonica), e sviluppando in tal senso [366] [366] Partendo dalla (10.158) R_x(τ) = 1T ∫^T ⁄ 2_{− T ⁄ 2}x^*(t)x(t + τ)dt possiamo scrivere

R_x(τ) = 1 T ^T ⁄ 2⌠⌡_{− T ⁄ 2}^∞⎲⎳_{n = −∞}X^*_n e^−j2πnFt^∞⎲⎳_{m = −∞}X_m e^{j2πmF(t + τ)}dt = = ^∞⎲⎳_{n = −∞}^∞⎲⎳_{m = −∞}X^*_nX_m1T e^j2πmFτ^T ⁄ 2⌠⌡_{− T ⁄ 2} e^{j2π(m − n)Ft}dt = ^∞⎲⎳_{n = −∞}|X_n|² e^j2πnFτ

in cui l’ultima uguaglianza è frutto della proprietà di ortogonalità degli esponenziali (2.3). la (10.158) si ottiene che l’autocorrelazione di x(t) ha espressione R_x(τ) = ∑^∞_{n = −∞}|X_n|² e^j2πnFτ, ovvero può essere espressa in serie di Fourier, e quindi è a sua volta periodica, come già osservato. La relativa densità di potenza P_x(f) risulta dunque pari a

(10.160) P_x(f) = F {R_x(τ)} =^∞⎲⎳_{n = −∞}|X_n|²δ(f − nF)

che costituisce una conferma del teorema di Parseval (10.13). A pag. 1 sono riportati alcuni esempi di autocorrelazione e densità di potenza per segnali periodici.

Componente continua

Come osservato a pag. 1, se il segnale può essere scritto come x(t) = x₀(t) + a in cui E{x₀(t)} = 0 ed a è una costante, si ottiene R_x(τ) = R_x₀(τ) + a² e dunque P_x(f) = F {R_x(τ)} = P_x₀(f) + a²δ(f), ossia la relativa densità spettrale presenta un impulso nell’origine di area a². Ovvero, dal punto di vista opposto, un impulso nell’origine di P_x(f) indica la presenza di una componente continua in x(t).

7.2.3 Processo armonico

Si tratta del segnale sinusoidale introdotto a pag. 1 e la cui fase iniziale è aleatoria, espresso come

(10.161) x(t, θ) = Acos(2πf₀t + θ)

in cui il parametro θ è una v.a. con d.d.p. uniforme tra − π e π, ovvero p_Θ(θ) = 12π rect_2π(θ). In tal caso x(t, θ) costituisce un processo ergodico (vedi § 6.3.7), la cui d.d.p.

p_X(x) = 1π√ A² − x²

è graficata a pagina 1.

Dato che a ciascuna realizzazione del processo armonico (ad esempio quella con θ = 0) corrisponde la medesima [367] [367] Infatti le diverse realizzazioni (10.161) al variare di θ differiscono solo per una traslazione temporale, a cui in frequenza corrisponde un termine di fase lineare, che non incide sulla P_x(f). densità di potenza [368] [368] Il risultato si ottiene applicando la (10.160) all’unica armonica presente, e considerando che la potenza totale P_x = A² 2 si distribuisce per metà a frequenza positiva e per metà negativa. P_x(f) = A² 4 [δ(f − f₀) + δ(f + f₀)], possiamo ottenere l’autocorrelazione R_x(t) (10.161) senza dover svolgere l’integrale (10.158), e neanche la media di insieme (10.153). Infatti, per il teorema di Wiener si ha

R_x(t) = F ⁻¹{ P_x(f)} = A² 4 [e^j2πf₀t + e^−j2πf₀t] = A²2 cos(2πf₀t)

Questo risultato conferma che l’autocorrelazione di un segnale periodico è periodica; riflettiamo dunque sulla circostanza che anche un seno, od un coseno con qualunque altra fase, avrebbe avuto la stessa R_x(t). Ciò è d’altra parte evidente, avendo tutti questi segnali uguale densità di potenza P_x(f).

7.2.4 Processo gaussiano bianco limitato in banda

Un processo n(t) è chiamato bianco quando la densità di potenza è costante in frequenza, ovvero quando si esprime come

P_n(f) = N₀ 2 rect_2W(f)

in cui W è l’occupazione di banda a frequenze positive. Per questo caso l’autocorrelazione vale

(10.162)
R_n(t) = F ⁻¹{ P_n(f)} = N₀W sinc(2Wt)

e possiamo pertanto constatare che si ottiene

R_n(0) = P_n = ⌠⌡^∞_−∞P_n(f)df = ⌠⌡^W_− WN₀ 2 df = N₀W = σ²_n

in cui l’ultima eguaglianza sussiste (vedi eq. (10.119) a pag. 1) in quanto l’assenza di impulsi nell’origine per P_n(f) corrisponde ad un n(t) a media nulla. Inoltre, dato che R_n(t) si azzera per t = ^k⁄_2W, osserviamo che campionando n(t) con periodo T_c = ¹⁄_2W si ottengono valori incorrelati, e se il processo è gaussiano, anche statisticamente indipendenti (vedi § 6.5.1). Questo risultato giustifica, almeno da un punto di vista teorico, una ipotesi che viene spesso fatta: quella di trovare, sovrapposti ai campioni di un segnale limitato in banda, dei campioni di rumore statisticamente indipendenti.

All’aumentare di W, R_n(t) tende a zero più rapidamente, cosicché il rumore si mantiene correlato per un tempo sempre minore, ovvero due campioni separati da uno stesso intervallo temporale t hanno una correlazione sempre minore. Un risultato simile vale anche più in generale, in quanto l’autocorrelazione R_x(t) di un qualsiasi processo a media nulla (tranne nel caso periodico, riconducibile ad una combinazione di processi armonici) tende a 0 con t → ∞, ovvero da un certo t in poi la correlazione è trascurabile.

Infine, se immaginiamo il rumore bianco limitato in banda come il risultato del transito di un processo gaussiano a banda infinita (quindi, con R_n(t) = δ(t)) attraverso un filtro passa basso ideale con H(f) = rect_2W(f) (vedi § 15.4.1), ci accorgiamo che la correlazione (10.162) tra campioni di rumore in uscita presi ad istanti diversi (t ≠ 0) è una diretta conseguenza della memoria introdotta dalla risposta impulsiva h(t) = 2W sinc(2Wt) sul segnale in transito, dato che l’operazione di convoluzione tra n(t) e h(t) rende i valori in uscita una combinazione lineare di quelli (passati) in ingresso (vedi § 3.4.3).

Esercizio Sia dato un processo gaussiano ergodico a media nulla e con densità di potenza P_x(f) = P_x2β β² + 4(πf)² in cui β = 0.2 e P_x = 5.

Esprimere la relativa funzione di autocorrelazione R_x(τ);
esprimere la d.d.p. p_X(x) di una v.a. x estratta dal processo ad un istante casuale;
esprimere vettore medio m_x e matrice di covarianza Σ_x di una coppia di v.a. x₁ e x₂ estratte con un intervallo τ, ovvero x₁ = x(t) e x₂ = x(t + τ), per un valore di τ = 10.

Svolgimento In base alla tabella al § 3.8.8 risulta che F ⁻¹⎧⎩ 2β β² + 4(πf)² ⎫⎭ = e^− β|t|, dunque

R_x(τ) = F ⁻¹{P_x(f)} = P_x e^− β|τ| = 5 ⋅ e^{− 0.2|τ|}
abbiamo evidentemente a che fare con una v.a. gaussiana, dunque p_X(x) = 1√ 2π σ_x e^{− (x − m_x)² 2σ²_x} in cui σ²_x = P_x = 5 in quanto a media nulla, e pari al massimo di R_x(τ) per τ = 0;
la coppia x₁x₂ è un vettore aleatorio gaussiano bidimensionale, il cui valor medio è nullo in base alla stazionarietà ed all’essere il processo a media nulla, mentre Σ_x è una matrice 2 × 2 sulla cui diagonale compare R_x(0) = σ²_x mentre nelle altre due posizioni compare la covarianza
σ_x₁x₂ = m^(1, 1)_x₁x₂(τ = 10) = R_x(τ = 10) = 5 ⋅ e^{− 0.2 ⋅ 10} = 0.68
dunque m_x = ⎡⎢⎣ 0 0 ⎤⎥⎦ e Σ_x = ⎡⎢⎣ 5 0.68 0.68 5 ⎤⎥⎦.

7.2.5 Processo di segnale dati

Al § 15.1.2 descriveremo un generico segnale numerico come una somma di repliche di una funzione g(t), ognuna moltiplicata per un diverso valore a_n rappresentativo delle informazioni da trasmettere:

(10.163) x(t) = ^∞⎲⎳_{n = −∞}a_ng(t − nT + θ)

La presenza della variabile aleatoria θ a distribuzione uniforme tra ± T2 (per cui p_Θ(θ) = 1T rect_T(θ)), rende x(t) un processo ergodico (vedi pag. 1).

Si mostrerà in appendice (§ 7.7.4) che, nelle ipotesi in cui le ampiezze a_n siano determinazioni di variabili aleatorie indipendenti ed identicamente distribuite, a media nulla e varianza σ²_A( [369] [369] Media m_A e varianza σ²_A sono qui riferite ai valori multilivello a^k (con k = 1, 2, ⋯, L) che un generico simbolo a_n può assumere, pesati con le rispettive probabilità p_k, ossia

m_A = ∑^L_k = 1p_ka^k e σ²_A = ∑^L_k = 1p_k(a^k − m_A)²

), la densità spettrale di potenza del processo (10.163) risulta

(10.164) P_x(f) = σ²_A E_g(f) T

mentre nel caso in cui gli a_n siano statisticamente dipendenti, e/o a media non nulla, il risultato è più complesso (vedi eq. (10.192)). Limitandoci ad interpretare il risultato semplice espresso dalla (10.164), notiamo che E_g(f) è la densità di energia di una singola replica di g(t), la cui ripetizione, con periodo T, fornisce una densità di potenza media E_g(f)T. Se ogni replica di g(t) è moltiplicata per una v.a. indipendente a media nulla e varianza (potenza) σ²_A, la densità di potenza P_x(f) aumenta di egual misura (vedi § 7.5.3).

Prev Sezione 7.1: Correlazione, covarianza e autocorrelazione Su Capitolo 7: Correlazione, densità spettrale e filtraggio Sezione 7.3: Stima spettrale Next