12.3 Modulazione angolare
In questo caso l’informazione contenuta nel messaggio
m(t) è impressa sulla portante modificandone la fase
α(t), ottenendo un segnale modulato
il cui inviluppo complesso (vedi eq.
(14.3)) vale
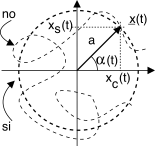
x(t) = a e jα(t) = xc(t) + jxs(t), dove
xc(t) = a cos α(t) e
xs(t) = a sin α(t).
Notiamo subito che a differenza della modulazione di ampiezza, il modulo di
x(t) è rigorosamente
costante, e la sua fase
α(t) può evolvere nel tempo unicamente su di una circonferenza di raggio
a. Si è già mostrato al §
11.2.2 come il legame tra messaggio
m(t) e fase dell’inviluppo complesso
α(t) possa essere descritto come modulazione di
fase (o
pm, phase modulation) qualora risulti
α(t) = kφm(t), oppure nei termini di una modulazione di
frequenza (o
fm) qualora si scelga
α(t) = 2πkf ∫t−∞m(τ)dτ, dove
kφ e
kf sono coefficienti di proporzionalità che
dosano l’intensità della modulazione introdotta.
La relazione che lega la
frequenza istantanea fi(t) ad
m(t) dipende dal legame tra
α(t) ed
m(t); ricordando la definizione (eq.
(14.6)) di
fi(t) come la derivata della
fase
istantanea ψ(t) = 2πf0t + α(t), ovvero
si ottiene la tabella a lato che riassume la dipendenza della fase
α(t) e della frequenza istantanea
fi(t) da
m(t) per entrambi i tipi di modulazione angolare. Le due alternative
pm e
fm sono quindi esaminate assieme, in quanto intercambiabili qualora si effettui
- una pm con m(t) pari all’integrale del messaggio informativo oppure
- una fm con m(t) pari alla derivata del messaggio informativo.
Prima di affrontare gli aspetti della generazione, ricezione, e determinazione della densità di potenza di un segnale modulato angolarmente, analizziamo due sue peculiarità.
Una caratteristica
fondamentale della modulazione angolare è che il segnale modulato
x(t) dipende da quello modulante
m(t) in modo fortemente
non lineare, e pertanto lo spettro di densità di potenza
Px(f) di
(14.48) non può essere calcolato allo stesso modo del caso
am. Infatti, l’inviluppo complesso di un segnale modulato angolarmente può essere espresso come:
da cui risulta evidente che, anche se
Pα(f) può essere espressa in funzione di
Pm(f) in base alle relazione di tab.
12.2, nulla può essere detto in generale per
Px(f), e dunque per
Px(f) = 14 Px(f − f0) + 14 Px( − f − f0) (eq.
(14.20)). Infatti, la presenza delle potenze della fase modulante
α(t) impedisce l’applicabilità del principio di sovrapposizione degli effetti, ovvero, anche se sono noti i risultati della modulazione per due diversi messaggi
x1(t) = FM{m1(t)} e
x2(t) = FM{m2(t)}, il risultato ottenibile modulando la loro somma
non è pari alla somma dei risultati individuali:
FM {m1(t) + m2(t)} ≠ FM{m1(t)} + FM{m2(t)}
La circostanza che
x(t) = a e jα(t) presenti un modulo costante pari ad
a, indipendentemente dall’ampiezza del segnale modulante, è particolarmente utile qualora per
m(t) siano previste forti variazioni di dinamica, come ad es. nel caso del segnale
fdm (pag.
1) utilizzato per trasmettere più canali telefonici. Infatti in questo caso, non essendo noto a priori il numero di canali effettivamente impegnati, la potenza del segnale
y(t) = ∑Nn = 1 BLU{mn(t), fn} ottenuto sommando i diversi canali (ognuno a modulazione
blu su di una diversa portante
fn) può variare di molto. Il segnale complessivo
y(t) viene dunque applicato all’ingresso di un modulatore
fm e trasmesso a piena potenza, senza subire distorsioni di non linearità (vedi §
8.3 e
13.3.3).
12.3.1 Generazione di un segnale a modulazione angolare
Il metodo
più diretto di generare un segnale
fm è quello di utilizzare un
vco (introdotto al §
12.2.2.2), ossia un oscillatore controllato in tensione, che produce il segnale
x(t) = a sin(ω0t + 2πkf ⌠⌡t−∞m(τ)dτ)
e dunque realizza proprio la funzione desiderata. D’altra parte, per effettuare una modulazione
pm per la quale
α(t) = kφm(t) si può usare un modulatore
fm a partire da una fase modulante
α(t) = 2πkf ∫t−∞m’(τ)dτ, ponendo
m’(t) = 12π kφkf ddt m(t). Un terzo metodo di modulazione è illustrato per un caso particolare, al §
12.4.6.
Entrambi i segnali
fm e
pm possono infine essere ottenuti mediante il modulatore in fase e quadratura (pag.
1) alimentato dalle c.a. di b.f.
xc(t) = cos α(t) e
xs(t) = sin α(t), come effettivamente accade in diversi casi di modulazione numerica, vedi il cap.
16.
12.3.2 Ricezione di un segnale a modulazione angolare
Di base, si può utilizzare un demodulatore
coerente in fase e quadratura (§
11.2.4) per ottenere le c.a. di b.f.
xc(t) ed
xs(t) a partire dal segnale modulato, e da queste ricavare la fase modulata
α(t) applicando la seconda eq.
(14.9), ovvero
α(t) = arctan2(xs, xc) (), ottenendo infine
m(t) invertendo le relazioni di tab.
12.2. Una soluzione del genere è tuttavia possibile solo nell’ambito di una implementazione
numerica, a causa della difficoltà realizzativa di un dispositivo circuitale che presenti esattamente la relazione non lineare di tipo arcotangente. Illustriamo quindi i due metodi più comunemente usati nel mondo
analogico.
12.3.2.1 Ricevitore a PLL
Al §
12.2.2.2 si è già mostrato l’uso del circuito
pll per l’aggancio della fase della portante di modulazione. Lo stesso schema può essere usato per
inseguire l’andamento temporale della fase di una portante modulata angolarmente, realizzando al contempo la funzione desiderata.
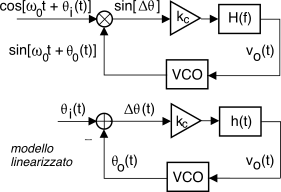
La figura a lato riporta lo schema generale di un
pll, in cui il
vco genera un segnale pari a
sin(ω0t + θo(t)), con
θo(t) = kv ∫t−∞vo(τ)dτ, mentre il segnale ricevuto ha la forma
x(t) = cos(ω0t + θi(t)). Lo schema può essere analizzato con i metodi dei controlli automatici, in quanto rappresenta un sistema che tenta di mantenere nullo l’errore
sinΔθ, con
Δθ(t) = θi(t) − θo(t) (vedi §
12.2.2.2); tale analisi si basa sulla
linearizzazione sinΔθ ≃ Δθ, valida per
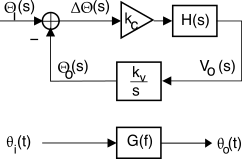
Δθ piccolo. In tal caso l’analisi di Laplace permette (vedi fig. sotto) di scrivere la relazione
che consente di esprimere
θo(t) (fase del
vco) come la versione
filtrata della fase della portante modulata
θi(t), da parte della risposta in frequenza
ad anello chiuso
G(f) = kckvH(s)s + kckvH(s)||s = j2πf
Ricordando che la fase
θo(t) del
vco corrisponde a
θo(t) = kv ∫t−∞vo(τ)dτ, possiamo constatare come il segnale
vo(t) al suo ingresso (ovvero l’uscita del filtro di loop
H(s)) corrisponda alla ricostruzione del messaggio modulante
m(t) nel caso di modulazione
fm! Pertanto, il segnale
vo(t) realizza la funzione di demodulazione di frequenza.
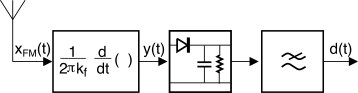
12.3.2.2 Ricevitore a discriminatore
Questa seconda architettura di demodulatore di frequenza si basa su di un fenomeno detto
conversione fm-am, di cui in figura
12.27-a) è mostrato il principio di funzionamento più semplice, e noto come
rivelatore a pendenza (
slope detector).
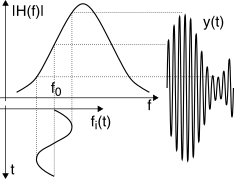
Un circuito risonante
accordato ad un frequenza maggiore di
f0 realizza una risposta in frequenza
H(f) il cui modulo aumenta in maniera pressoché lineare nella banda di segnale, simulando così l’
effetto di una derivata (vedi §
3.6). La figura mostra come, al variare della frequenza istantanea
fi(t) = fo + kfm(t), l’ampiezza del segnale (passabanda)
y(t) uscente dal derivatore
vari in misura del valore (tempo variante) di
|H(f)|f = fi(t), ottenendo così un segnale modulato
in ampiezza dalle stesse variazioni di
fi(t), ovvero di
m(t). La figura
12.27-b) mostra quindi uno schema che utilizza il fenomeno descritto per ricostruire il segnale modulante
m(t) a partire da
y(t) mediante un semplice demodulatore di inviluppo (§
12.2.5). Svolgendo infatti i passaggi, il segnale uscente dal derivatore risulta pari a
y(t) = 12πkf ddt a cos (2πf0t + 2πkf ⌠⌡t−∞ m(τ)dτ) = = 12 πkf (2πf0 + 2πkfm(t)) a sin (2πf0t + 2πkf ⌠⌡t−∞ m(τ)dτ)
che corrisponde ad un segnale modulato sia angolarmente che in ampiezza, ed in particolare la cui ampiezza risulta
a(t) = a (f0⁄kf + m(t)). Pertanto con una scelta opportuna di
f0⁄kf la modulazione di ampiezza è riconducibile al caso
bld-pi (§
12.1.1.2), e quindi il messaggio
m(t) può essere recuperato mediante un demodulatore d’inviluppo (§
12.2.5).
Il risultato ottenuto è valido purché il segnale modulato
x(t) sia esso stesso privo
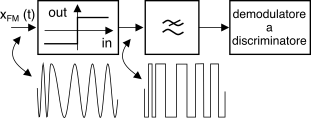
di variazioni di ampiezza: per questo motivo il derivatore è spesso preceduto da un blocco
squadratore, che produce una versione, appunto, "squadrata" del segnale ricevuto e quindi priva di modulazione di ampiezza. Essendo lo squadratore fortemente non lineare, in uscita saranno presenti, oltre al segnale originario, anche componenti centrate a frequenze multiple di quella della portante, che vengono rimosse mediante un filtro passa basso posto a valle dello squadratore.
12.3.3 Densità spettrale di segnali a modulazione angolare
Come già osservato a pag.
1, la relazione
(14.50) che esprime l’inviluppo complesso di un segnale modulato angolarmente nei termini di una serie di potenze
non può essere utilizzata in modo diretto per ottenere quella dello spettro di densità di potenza
Px(f) del segnale modulato in funzione di una generica fase modulante
α(t); ciononostante, la
(14.52) costituisce comunque un punto di partenza per analizzare altri aspetti della situazione.
Osserviamo innanzitutto che, essendo
|x(t)| = a, la sua potenza totale ha sempre valore
Px = a2, indipendentemente da
α(t), e dunque
Px = a22. Inoltre, la presenza nella
(14.52) di potenze di
α(t) di qualunque ordine sembrerebbe indicare che
Px(f) abbia una banda infinita: in realtà la presenza dei fattoriali a denominatore fa sì che la serie possa essere troncata ad un certo ordine
N < ∞, e dunque
x(t) sia da considerare limitato in banda.
Per speculare sull’influenza di
α(t) sul segnale modulato, notiamo che quanto più
|α(t)| è piccolo, tanto prima la
(14.52) può essere troncata con errori trascurabili; se poi
α(t) si mantiene sempre
molto piccolo, ci si può limitare al solo primo termine (
n = 1), dando così luogo ad un comportamento
lineare, dato che in tal caso si ottiene
x(t) = a(1 + jα(t)). Se viceversa
α(t) assume valori
molto elevati, e quindi (
14.52) comprende parecchi termini, subentra un secondo aspetto peculiare dell’
fm, indicato come
conversione ampiezza → frequenza, che può essere descritto tenendo conto che in base alla relazione
fi(t) = f0 + kfm(t), la frequenza istantanea presenta scostamenti rispetto ad
f0 direttamente proporzionali alle ampiezze di
m(t), e quindi
l’andamento della densità di potenza
Px(f) in funzione di
f riflette quello (funzione di
m) della densità di probabilità di
pM(m) che descrive le ampiezze di
m(t), come torneremo ad approfondire al §
12.3.3.3. Infine, a valori intermedi della dinamica di
α(t) corrisponde una
Px(f) che sarà una
via di mezzo tra i due casi estremi discussi, e che pertanto possono essere pensati come
casi limite tra cui porre la densità di potenza effettiva.
Dato che la natura non lineare della modulazione angolare rende necessario studiare ogni caso individualmente, il calcolo di Px(f) viene svolto nel seguito per il caso particolare di un segnale m(t) sinusoidale, considerando le due possibilità estreme di α(t) molto piccolo o molto grande, ed i risultati vengono quindi estrapolati per approssimare altre situazioni.
12.3.3.1 Segnale modulante sinusoidale
Per questo calcolo esprimiamo il segnale modulante come m(t) = cos(2πwt), con w che indica la frequenza di modulazione. L’espressione della fase modulante α(t) e della relativa frequenza istantanea fi(t) = f0 + 12π ddt α(t) per il segnale modulato x(t) = a cos(2πf0t + α(t)) risulta allora quella riportata alla tabella seguente, per i casi di modulazione di fase e di frequenza, assieme all’espressione della massima deviazione di fase Δα = max{|α(t)|} e di frequenza Δf = max{|fi(t) − f0|}.
| |
|
α(t) |
|
fi(t) |
Δα |
Δf |
| |
|
kφm(t) = kφ cos(2πwt) |
|
f0 − wkφ sin(2πwt) |
kφ |
wkφ |
| |
|
2πkf ∫t−∞m(τ)dτ = kfw sin(2πwt) |
|
f0 + kf cos(2πwt) |
kfw |
kf |
Osserviamo che in entrambi i casi sia
α(t) che
fi(t) variano sinusoidalmente con frequenza
w; nel caso
pm l’entità di
Δf aumenta con
w, mentre nell’
fm la
Δα diminuisce con
w. Nel seguito si farà riferimento all’
indice di modulazione angolare β, corrispondente alla massima escursione della fase
Δα, che risulta:
β = ⎧⎨⎩ kφ (PM) kfw (FM)
Con questa convenzione, possiamo trattare congiuntamente entrambi i casi
pm ed
fm riscrivendo l’inviluppo complesso come
x(t) = a e jα(t) = a e jβsin(2πwt)
Notiamo ora che
x(t) è periodico di periodo
1w, e dunque per esso vale lo sviluppo in serie di Fourier (§
2.2)
x(t) = a ∑∞n = −∞Xne j2πnwt, i cui coefficienti sono definiti come
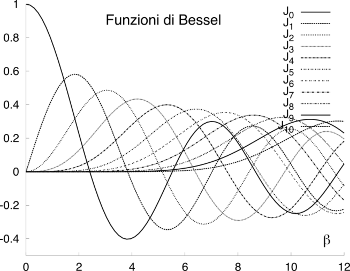
ovvero sono pari alle
funzioni di Bessel del
primo tipo, ordine
n ed argomento
β. Queste hanno l’andamento mostrato alla figura
12.29,
in cui sono riportate anche le proprietà che le caratterizzano. I valori di
Xn si ottengono quindi tracciando una linea verticale nel diagramma di figura in corrispondenza del valore adottato per
β, e individuando il valore di ciascuna
Jn per quel
β.
Osserviamo ora che in presenza di un valore di
β elevato, in base all’ultima proprietà mostrata in fig.
12.29 ovvero che
Jn(β) ≃ 0 con
n > β se
β≫1, le funzioni di Bessel di ordine
n > β sono praticamente nulle: è quindi lecito in tal caso limitare lo sviluppo in serie di Fourier di
x(t) ai primi
β termini (positivi e negativi), ovvero
xFM(t) ≃ aβ⎲⎳n = − βJn(β) e j2πnwt F ⟹ XFM(f) ≃ aβ⎲⎳n = − βJn(β) δ(f − nw)
Pertanto il segnale modulato
x(t) = ℜ{x(t)e jω0t} risulta pari a
ossia è costituito da
2β + 1 cosinusoidi a frequenza
f0±nw centrate
attorno ad
f0, e dunque il relativo spettro di densità di potenza ha espressione
ed è formato da impulsi centrati a frequenza
f = ±f0±nw.
Osserviamo che in base alla proprietà
∑ + ∞n = −∞J 2n(β) = 1, estendendo la somma in
(14.55) per
−∞ > n > ∞ ed integrando su
f si ottiene un risultato già noto, ovvero la potenza totale
Px eguaglia quella della portante non modulata, pari a
a22, indipendentemente dall’indice di modulazione
β.
Modulazione a basso indice
Come anticipato al §
12.3.3 e mostrato in fig.
12.29, qualora
β ≪ 1 le funzioni di Bessel
Jn(β) con
n > 1 presentano valori che possono essere trascurati. Pertanto in tal caso
x(t) occupa una banda
B ≃ 2w, in modo del tutto simile all’
am-bld.
Modulazione ad alto indice
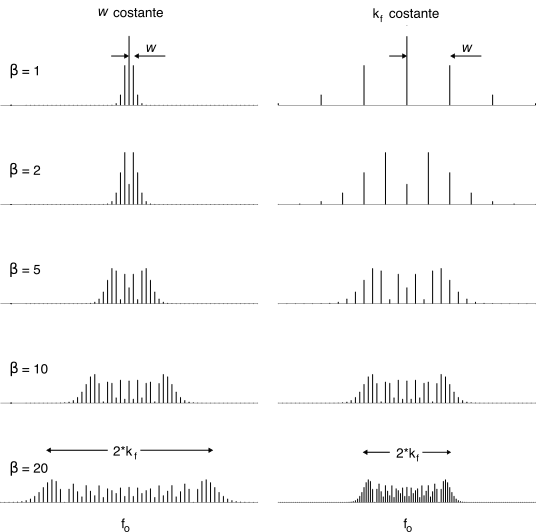
All’aumentare di
β = kfw nella
(14.55) aumenta il numero dei termini rilevanti, e la fig.
12.30 mostra l’aspetto di
|X(f)| per
f > 0 () calcolato per valori di
β crescenti, mantenendo fisso
w (a sinistra) oppure
kf (a destra). Osserviamo che
- mantenendo w fisso ed aumentando kf, ovvero l’ampiezza di m(t), il numero di righe spettrali a frequenza f0±nw aumenta, occupando una banda crescente, che per β molto grande si estende da f0 − βw a f0 + βw, dato che Jn(β) ≃ 0 per n > β;
- mantenendo kf fisso e diminuendo w, ossia la frequenza modulante, la banda occupata tende a ridursi, mentre le nuove righe spettrali a frequenza f0±nw si infittiscono. Per w → 0 si ha β → ∞ mentre la spaziatura tra le righe spettrali tende ad annullarsi, producendo una densità spettrale praticamente continua.
Notiamo che in entrambi i casi all’aumentare di
β la banda occupata a frequenze positive è bene approssimata dal valore
B = 2βw = 2 kfw ⋅ w = 2kf, ossia pari al doppio della massima deviazione di frequenza
istantanea Δf, vedi la tabella a pag.
1.
12.3.3.2 Regola di Carson
Come appena discusso la modulazione
fm da parte di un tono sinusoidale a frequenza
w produce un segnale modulato
x(t) la cui banda varia tra
2w e
2kf nei casi di indice di modulazione
β rispettivamente basso od alto. Una formula in grado di esprimere questo tipo di relazione è
nota come
regola di Carson, in grado di tener conto di entrambi i fattori che concorrono alla determinazione della banda, e che fornisce i valori esatti sia per
β ≪ 1, che per
β → ∞, in entrambi i casi in cui sia
kf ad aumentare, o
w a diminuire.
Sebbene questo risultato si riferisca al caso di
m(t) = cos(2πwt), la
(14.56) viene spesso adottato come una buona approssimazione anche per altri tipi di segnali modulanti, come illustrato appresso.
Si riferisce ad un segnale
fm per il quale
m(t) è la combinazione di più sinusoidi a frequenza
wi ed ampiezza
kif. In tal caso la trattazione matematica si complica, e perviene al risultato che nel segnale modulato
x(t) compaiono, oltre a componenti spettrali già analizzate e relative a ciascuna
wi, centrate in
f0 e spaziate da multipli di
wi, anche componenti spaziate a frequenze somma e differenza delle combinazioni dei multipli delle
wi. In questo caso l’occupazione di banda è approssimata riscrivendo la
(14.56) come
BC = 2wM(βM + 1) in cui
wM = maxi{wi} è la più grande delle frequenze modulanti e
βM = ΔfM⁄wM è l’indice di modulazione
equivalente per questo caso, avendo definito
ΔfM = ∑ikif come la massima deviazione della frequenza istantanea
Δf.
Modulazione per segnali qualsiasi
Nel caso di un segnale modulante generico, limitato in banda tra − W e W, e che produce da una deviazione massima della frequenza istantanea Δf = kf ⋅ max{|m(t)|}, l’occupazione di banda è approssimata riscrivendo nuovamente la regola di Carson come BC ≃ 2W(βs + 1) con βs = ΔfW.
L’applicazione della regola di Carson mostra che la banda occupata dal segnale modulato può risultare
βs + 1 volte più estesa di quella
W del segnale modulante, un comportamento del tutto nuovo rispetto a quanto avviene nel caso dell’
am. Nonostante possa sembrare un aspetto negativo, al §
14.4.2 si mostra come una maggiore occupazione di banda consenta di migliorare l’
snr dopo demodulazione, superando in tal modo le prestazioni ottenibili nel caso
am. Al contrario, se
βs≪1 il comportamento si avvicina molto a quello lineare (vedi appendice
12.4.6).
12.3.3.3 Densità spettrale per FM ad alto indice
Riprendiamo il ragionamento iniziato al §
12.3.3 e relativo a come la densità di probabilità
pM(m) del segnale modulante si rifletta sulla densità di potenza
Px(f) del corrispondente segnale
fm nel caso di modulazione ad alto indice, ovvero qualora
βs ≫ 1. In questo caso, la frazione di potenza totale
Px = a22 del segnale
fm che si distribuisce tra le frequenze
f1 ed
f2 è pari alla frazione di tempo per cui la frequenza istantanea
fi(t) = f0 + kf m(t) permane nello stesso intervallo, ovvero pari alla frazione di tempo per cui il segnale modulante
m(t) assume valori compresi tra
m1 = f1 − f0kf e
m2 = f2 − f0kf. Tale frazione è proprio pari alla probabilità di trovare
m1 ≤ m(t) ≤ m2, ovvero
Prob{m1 ≤ m(t) ≤ m2} = ∫m2m1 pM(m)dm, dove
pM(m) è la densità di probabilità che descrive il processo modulante.
Si può affermare dunque che qualora si generi un segnale
fm ad alto indice a partire da un processo con densità di probabilità nota, lo spettro di densità di potenza del segnale modulato acquisisce l’andamento proprio della densità di probabilità del processo modulante, indipendentemente dal suo spettro di densità di potenza. Tale conclusione mantiene validità purché
β≫1; nel caso contrario, sono validi i ragionamenti sviluppati al §
12.3.3.5.
Esempio Un processo
m(t) limitato in banda
± W e con con d.d.p. uniforme
pM(m) = 1ΔMrectΔM(m) modula ad alto indice una portante a frequenza
f0 ed ampiezza
a, con un coefficiente di modulazione
kf. Determinare la
Px(f) del segnale modulato.
R: Notiamo che la frequenza istantanea
fi rimane limitata tra
f0 − ΔM2kf e
f0 + ΔM2kf. Inoltre, la potenza totale deve risultare ancora pari a
a22. Pertanto si ottiene :
Px(f) = a24ΔMkf[rectΔMkf(f − f0) + rectΔMkf(f + f0)]
Esempio Nel caso in cui
m(t) sia sinusoidale, con fase iniziale aleatoria a distribuzione uniforme,
m(t) è una realizzazione di un processo armonico (pag.
1), e dunque per
β≫1 risulterà
Px(f) = a21 − (f ⁄ kf)2, con l’andamento rappresentato dalla fig.
6.12 a pag.
1, ovvero il quadrato dell’andamento a cui tendono (per
β → ∞) i grafici in basso di fig.
12.30. Pertanto le righe spettrali, addensandosi, tendono a disporsi in accordo all’andamento della densità di probabilità
pM(m) del processo armonico.
12.3.3.4 Indice di modulazione per processi
Nel caso in cui non sia nota la d.d.p. del processo modulante, ma solo la sua potenza, oppure qualora non sussista la condizione di alto indice
βs≫1, oppure ancora non sia possibile definire il valore della massima deviazione di frequenza
Δf = kf ⋅ max{|m(t)|} come ad esempio per
m(t) gaussiano, allora l’occupazione di banda può ancora essere approssimata mediante un’ultima variazione della regola di Carson, che viene ora applicata dopo aver definito un indice di modulazione
βp per processi come
βp = ⎧⎨⎩ σα (PM) σfW (FM)
in cui
W è la banda a frequenze positive del segnale modulante,
σf = kf√Pm rappresenta la deviazione standard della frequenza istantanea, e
σα = kφ√Pm è la deviazione standard della fase modulante. L’applicazione della regola di Carson con il nuovo valore di
βp fornisce un risultato che non indica più la banda
totale occupata, ma individua una
banda efficace entro cui
Px(f) è in larga parte (ma non completamente) contenuta (vedi anche
25.2).
Nel caso in cui non risulti β ≫ 1, lo spettro di potenza del segnale modulato FM torna a dipendere da quello del segnale modulante, e si ricade nella trattazione che segue.
12.3.3.5 Densità spettrale per FM a basso indice
In questo caso si suppone l’indice di modulazione
β piccolo a sufficienza, in modo che lo sviluppo in serie dell’inviluppo complesso del segnale modulato possa essere arrestato ai primi termini. Sotto opportune ipotesi, si può mostrare che vale il risultato
Px(f) ≃ a2e− σ2α⎡⎣δ(f) + Pα(f) + 12 Pα(f) * Pα(f) + 13! Pα(f) * Pα(f) * Pα(f) + ⋯⎤⎦
avendo indicando con
σ2α la varianza della fase modulata e con
Pα(f) il relativo spettro di densità di potenza, pari rispettivamente a
|
|
Pα(f) |
|
σ2α |
| |
|
k2φPm(f) |
|
k2φPm |
| |
|
k2fPm(f)f2 |
|
k2f ∫w − wPm(f)f2df |
Osserviamo che se kφ (o kf) tende a zero, Px(f) si riduce ad un impulso, corrispondente alla portante non modulata. All’aumentare di kφ (o kf), aumenta anche σ2α e dunque il termine e− σ2α diminuisce, riducendo la concentrazione di potenza a frequenza portante. Dato che risulta comunque Px = a2, la potenza residua si distribuisce sugli altri termini, rappresentati da Pα(f) e delle sue autoconvoluzioni. E’ immediato notare come, al crescere di kφ (o kf), cresca la banda.
In appendice
12.4.6 è illustrata una tecnica di modulazione per segnali FM modulati a basso indice.