Somma e prodotto tra segnali aleatori

Prev Sezione 7.4: Filtraggio di segnali e processi Su Capitolo 7: Correlazione, densità spettrale e filtraggio Sezione 7.6: Filtro adattato Next

7.5 Operazioni elementari sui segnali

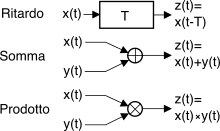
Al § 5.2 abbiamo visto come gli elementi filtranti possano essere realizzati mediante una combinazione delle tre operazioni elementari mostrate in figura, ovvero ritardo, somma e prodotto.

Prima di proseguire, approfondiamo dunque il risultato della combinazione di segnali certi ed aleatori mediante gli operatori introdotti. Iniziamo osservando che per i due casi di somma e prodotto si possono verificare le seguenti combinazioni:

x(t) segnale certo e y(t) processo aleatorio: il risultato è (in generale) un processo non stazionario, infatti ora le medie d’insieme dipendono, istante per istante, dal valore che il segnale certo assume in quell’istante;
x(t) segnale periodico e y(t) processo aleatorio: si ottiene un processo detto ciclostazionario, in quanto anche se le statistiche variano nel tempo, esse assumono valori identici con periodicità uguale a quella del segnale certo;
x(t) segnale costante pari ad a e y(t) processo aleatorio: z(t) è un processo della stessa natura di y(t), con media m_z pari alla somma (od il prodotto) tra m_y ed a, potenza P_z = P_y + a² (oppure ⋅ a²), e autocorrelazione R_z(τ) = R_y(τ) ⋅ a² (oppure +a²).

Notiamo inoltre che spesso si può trattare un segnale periodico alla stregua di un processo, semplicemente ipotizzando per lo stesso una fase uniforme nell’arco di un periodo, in modo da ricondursi al caso del processo armonico, vedi § 7.2.3. Dunque, nel seguito trattiamo solo il caso dei processi.

7.5.1 Ritardo

Questo costituisce un caso particolare di canale perfetto (pag. 1), ed analiticamente corrisponde alla convoluzione con un impulso traslato z(t) = x(t) * δ(t − T). Pertanto, l’unica cosa che si modifica [384] [384] Vedi §§ 87 e 3.4.4. in uscita è lo spettro di fase, in cui compare un termine lineare, ovvero Z(f) = X(f) ⋅ e^−j2πfT, mentre valor medio, autocorrelazione e densità di potenza/energia restano invariate, così come non cambiano la varianza e la d.d.p. per il caso di processi.

7.5.2 Somma tra segnali aleatori

Procediamo nel calcolo delle grandezze rappresentative avvalendoci (a parte per il valor medio) della ipotesi di indipendenza statistica tra x(t) e y(t):

Valore medio

m_z = E{x(t) + y(t)} = E{x(t)} + E{y(t)} = m_x + m_y

Notiamo che questo risultato è valido anche in assenza di indipendenza statistica [385] [385] Infatti in virtù della proprietà distributiva è possibile la saturazione di una v.a. alla volta, ovvero

⌠⌡⌠⌡(x + y)p(x, y) dxdy = ⌠⌡⌠⌡x ⋅ p(x, y) dxdy + ⌠⌡⌠⌡y ⋅ p(x, y) dxdy = = ⌠⌡x ⋅ p(x) dx + ⌠⌡y ⋅ p(y) dy

Potenza totale

P_z = E{(x(t) + y(t))²} = E{x²(t)} + E{y²(t)} + 2E{x(t) ⋅ y(t)} = = P_x + P_y + 2m_xm_y

dato che per processi statisticamente indipendenti la d.d.p. congiunta p_XY(x, y) si fattorizza nel prodotto delle marginali p_X(x)p_Y(y), così come si fattorizza il valore atteso del prodotto [386] [386] Infatti risulta

E{x(t) ⋅ y(t)} = ⌠⌡⌠⌡x ⋅ y ⋅ p(x, y)dxdy = ⌠⌡x ⋅ p(x)dx ⋅ ⌠⌡y ⋅ p(y)dy = = E{x(t)}E{y(t)} = m_xm_y

; anche i prossimi risultati valgono unicamente sotto l’ipotesi di indipendenza statistica.

Varianza

Dalle due relazioni precedenti otteniamo

σ²_z = E{(z(t) − m_z)²} = P_z − (m_z)² = P_x + P_y + 2m_xm_y − (m_x + m_y)² = = P_x − (m_x)² + P_y − (m_y)² = σ²_x + σ²_y

Autocorrelazione

R_z(τ) = E{z(t)z(t + τ)} = E{(x(t) + y(t))(x(t + τ) + y(t + τ))} = = E{x(t)x(t + τ)} + E{y(t)y(t + τ)} + E{x(t)y(t + τ)} + E{x(t + τ)y(t)} = = R_x(τ) + R_y(τ) + 2m_xm_y

dato che per processi indipendenti, stazionari e congiuntamente ergodici [387] [387] La proprietà di ergodicità congiunta corrisponde a verificare le condizioni ergodiche anche per i momenti misti m^(1, 1)_XY(x, y) relativi a coppie di valori estratti da realizzazioni di due differenti processi. risulta E{x(t)y(t + τ)} = R_xy(τ) pari cioè al prodotto delle medie m_xm_y, vedi eq. (10.151). Osserviamo anche come per τ = 0 si ritrovi il valore della potenza totale P_z.

Spettro di densità di potenza

P_z(f ) = F {R_z(τ)} = P_x(f) + P_y(f) + 2m_xm_yδ(f)

e rimarchiamo ancora una volta che in caso di processi non indipendenti il risultato non è valido.

Densità di probabilità

Nel caso di x(t) ed y(t) indipendenti si ottiene che il processo somma è caratterizzato da una densità di ampiezza pari a [388] [388] Dimostriamo la (10.170) con un ragionamento forse poco ortodosso ma efficace. Dalla definizione di d.d.p. abbiamo che z = x + y risulta compresa tra z e z + dz con probabilità p_Z(z)dz, ma affinché ciò accada è necessario che, per ogni possibile valore di x, risulti y = z − x; per l’ipotesi di indipendenza statistica tra x ed y ciò avviene con probabilità congiunta p_X(x)dx ⋅ p_Y(z − x)dz. Per ottenere p_Z(z)dz occorre quindi sommare la probabilità congiunta su tutti i possibili valori di x, ovvero p_Z(z)dz = ∫_{Ω_X}p_X(x)p_Y(z − x)dxdz in cui Ω_X è lo spazio campione per la v.a. x. Pertanto in definitiva si ottiene p_Z(z) = ∫_{Ω_X}p_X(x)p_Y(z − x)dx che corrisponde alla convoluzione espressa nel testo.

(10.170) p_Z(z) = ^∞⌠⌡_−∞p_X(θ)p_Y(z − θ)dθ = p_X(x) * p_Y(y)

Tale risultato conferma quello già ottenuto al § 6.2.5 e relativo alla somma di variabili aleatorie, ovvero che la d.d.p. di una somma di v.a. indipendenti si ottiene per convoluzione tra le densità dei termini della somma.

Notiamo infine che se vengono sommati due processi gaussiani il risultato è ancora gaussiano, come discusso al § 6.5.2: infatti la convoluzione tra funzioni gaussiane è ancora una gaussiana, con media pari alla somma delle medie, e varianza alla somma delle varianze.

7.5.3 Prodotto tra segnali aleatori

Anche per il prodotto tra segnali valgono le considerazioni svolte al § 7.5. Qualora i fattori x(t) ed y(t) del prodotto z(t) siano processi statisticamente indipendenti, stazionari e congiuntamente ergodici, si ha

Valor medio

m_z = E{z(t)} = E{x(t)y(t)} = E{x(t)} E{y(t)} = m_x ⋅ m_y

dato che come già osservato risulta p_XY(x, y) = p_X(x)p_Y(y) permettendo così la fattorizzazione del valore atteso del prodotto, ossia

∬ x y p(x, y)dxdy = ∫ x p(x)dx ⋅ ∫ y p(y)dy

Potenza totale

P_z = E{z²(t)} = E{x²(t)y²(t)} = E{x²(t)} E{y²(t)} = P_x ⋅ P_y

Varianza

σ²_z = E{(z(t) − m_z)²} = P_z − (m_z)² = P_x ⋅ P_y − (m_x ⋅ m_y)²

Funzione di autocorrelazione

R_z(τ) = E{z(t)z(t + τ)} = E{x(t)y(t)x(t + τ)y(t + τ)} = = E{x(t)x(t + τ)} E{y(t)y(t + τ)} = R_x(τ) ⋅ R_y(τ)

In particolare, notiamo che l’incorrelazione di uno dei due processi, per un certo valore di τ, provoca l’incorrelazione del prodotto, allo stesso istante τ.

Spettro di densità di potenza

P_z(f) = F {R_z(τ)} = F {R_x(τ) ⋅ R_y(τ)} = P_x(f) * P_y(f)

ossia è pari alla convoluzione tra le densità spettrali dei fattori. Notiamo quindi che la densità di potenza del prodotto presenta una occupazione di banda maggiore di quella dei singoli fattori.

Densità di probabilità

Si calcola con le regole per il cambiamento di variabile, illustrate al § 6.4. Nel caso in cui i due processi x e y siano statisticamente indipendenti, il risultato è [389] [389] Dimostriamo la (10.171) ricorrendo al metodo illustrato al § 6.4.2, scrivendo il sistema (10.134) come ⎧⎨⎩ z = xy w = y in modo che la trasformazione inversa risulti ⎧⎨⎩ x = z ⁄ w y = w . A questo punto si ottiene la matrice Jacobiana J = ⎡⎢⎣ ∂x∂z ∂x∂w ∂y∂z ∂y∂w ⎤⎥⎦ come ⎡⎢⎣ ¹⁄_w ^z⁄_w² 0 1 ⎤⎥⎦ a cui corrisponde il modulo del determinante (jacobiano) |det(J)| = 1|w|. Dunque la d.d.p. congiunta di z e w si ottiene come p_ZW(z, w) = |det(J)| ⋅ p_XY(x, y = f(z, w)) = 1|w| ⋅ p_XY⎛⎝zw, w⎞⎠ = 1|w| ⋅ p_X⎛⎝zw⎞⎠p_Y(w) in virtù della indipendenza statistica tra x e y. Non resta quindi che saturare la p_ZW(z, w) rispetto a w, ovvero p_Z(z) = ∫1|w| ⋅ p_X⎛⎝zw⎞⎠p_Y(w)dw, che corrisponde alla (10.171) qualora avessimo posto θ = x anziché w = y.

(10.171) p_Z(z) = ^∞⌠⌡_−∞p_X(θ) p_Y⎛⎝zθ⎞⎠ dθ|θ|

7.5.4 Stima della autocorrelazione

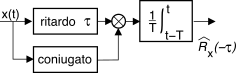
Come primo esempio dell’uso degli operatori elementari, la figura che segue mostra l’architettura di uno schema di elaborazione idoneo a effettuare una stima [390] [390] Si tratta di una stima (vedi § 6.6.3) in quanto l’intervallo di integrazione T è limitato. ^R_x(τ) della funzione di autocorrelazione (§ 7.1.4) di un segnale x(t) per un anticipo τ assegnato: infatti calcola ^R_x(−τ) = 1T ∫^T_t − Tx^*(t)x(t − τ)dt per τ ≥ 0, da cui ^R_x(τ) si ottiene applicando l’eq. (10.159). Il blocco integratore è un filtro passa-basso con una h(t) = 1T rect_T(t).

Variando τ si ottiene ^R_x(τ) per i diversi valori dell’argomento, e se x(t) è stazionario possiamo calcolare ^P_x(f) = F {^R_x(τ)}; se infine x(t) è un membro di un processo ergodico, ^P_x(f) rappresenta una stima della densità di potenza per una qualunque realizzazione.

Prev Sezione 7.4: Filtraggio di segnali e processi Su Capitolo 7: Correlazione, densità spettrale e filtraggio Sezione 7.6: Filtro adattato Next