19.2 Collegamenti in cavo
Iniziamo l’analisi dei mezzi trasmissivi con la descrizione delle caratteristiche e delle prestazioni dei cavi in rame, utilizzati fin dall’inizio della storia della trasmissione allo scopo di recapitare a distanza i segnali in forma elettrica. Il risultato più rilevante è senz’altro il manifestarsi dell’effetto pelle, che determina (per f > 100 KHz) una attenuazione in dB proporzionale a √f. La sezione è completata da una breve catalogazione dei cavi usati per telecomunicazioni.
19.2.1 Costanti distribuite, grandezze derivate, e condizioni generali
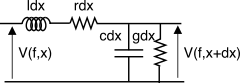
Un conduttore elettrico uniforme e di lunghezza infinita è descritto in base ad un modello cosiddetto a
costanti distribuite in quanto espresso nei termini delle costanti
primarie resistenza
r, conduttanza
g, capacità
c e induttanza
l per unità di lunghezza, di cui in figura
è fornita una rappresentazione nei termini della rete due porte (§
18.1.2) corrispondente ad una sezione di
lunghezza infinitesima del cavo. A partire dalle costanti primarie sono quindi definite due grandezze derivate, l’
impedenza caratteristica Z0(f) e la
costante di propagazione γ(f), da cui ottenere un modello di rete due porte equivalente
all’intero collegamento in cavo.
Rappresenta il rapporto tra
V(f) ed
I(f) in un generico punto del cavo, ed è definita come
permettendo di scrivere
I(f) = V(f)Z0(f)
Il rapporto tra valori di tensione presenti in due punti distanti
d di un cavo di lunghezza infinita viene espresso come
V(f, x + d) = e− γ(f)d V(f, x)
in cui la dipendenza da
f dovuta al cavo
è indicata come
costante di propagazione.
Qualora il cavo di lunghezza
d sia chiuso ai suoi estremi su di un generatore con impedenza
Zg(f) e su di un carico
Zc(f), risultano definiti i
coefficienti di riflessione del generatore e del carico:
Osserviamo che qualora
Zg(f) = Zc(f) = Z0(f) si ottiene
rg(f) = rc(f) = 0.
L’impedenza vista dai morsetti di
ingresso e di
uscita di un cavo interposto tra generatore e carico vale rispettivamente
Allo stesso tempo la funzione di trasferimento
intrinseca (§
18.1.2) risulta
Condizioni di adattamento
Corrispondono ad avere
a cui corrisponde
assenza di distorsione lineare (§
8.2), dato che in tal caso le
(21.164) forniscono
rg(f) = rc(f) = 0, e dunque dalle
(21.165) si ottiene che
Zi(f) = Zu(f) = Z0(f)
e la
(21.166) diviene
Hq(f) = Vq(f)Vi(f) = 2 e− dγ(f)
Pertanto il verificarsi delle condizioni di adattamento
(21.167) implica che il cavo
si comporta come se avesse lunghezza
infinita. Come ulteriore conseguenza troviamo che
Hi(f) = Zi(f)Zg(f) + Zi(f) = 12 (vedi §
18.1.2) e dato che
Rg(f) = Ru(f), per il guadagno disponibile (eq.
(21.127) pag.
1) si ottiene
Qualora i valori delle costanti primarie verifichino la relazione
r ⋅ c = l ⋅ g (nota come
condizione di Heaviside) le (
21.162) e (
21.163) si semplificano, implicando
γ(f) = √rg + j2πf√lc e Z0(f) = √rg = √lc = R0
Pertanto le parti reale
α(f) ed immaginaria
β(f) di
γ(f) divengono rispettivamente costante e linearmente crescente con la frequenza, realizzando così le condizioni di un canale perfetto (pag.
1) per il termine
e− dγ(f) che compare in
Hq(f); dato inoltre che l’impedenza caratteristica
Z0(f) = R0 è ora solamente resistiva ed indipendente dalla frequenza, diviene semplice realizzare la condizione di adattamento
(21.167), così come quella
Zc(f) = Z * g(f) di massimo trasferimento di potenza (§
18.1.1.3), oltre ad implicare
rg(f) = rc(f) = 0, e quindi
Hq(f) = 2 e− dα(f) e− jdβ(f) = 2 e− d√rg e− jd2πf√lc
In definitiva la risposta in frequenza complessiva per questo caso vale
H(f) = Hi(f) Hq(f) Hu(f) = 12 2 e− d√rg e− jd2πf√lc 12 = 12 e− d√rg e− jd2πf√lc
dunque equivalente ad un canale perfetto con guadagno
G = 12 e− d√rg e ritardo
tR = d√lc; al contempo l’attenuazione disponibile risulta indipendente da
f, e pari a
Ad(f) = 1 ⁄ Gd(f) = e2d√rg
19.2.2 Trasmissione in cavo
In generale le costanti primarie del cavo
non soddisfano le condizioni di Heaviside, e le impedenze di chiusura
non sono adattate. In tal caso si ha
rg(f) ≠ 0 e/o
rc(f) ≠ 0, e devono essere applicate le (
21.165) e (
21.166).
Se il cavo è sufficientemente lungo da poter considerare
|e− 2dγ(f)| = e− 2dα(f) ≪ 1
le (
21.165) divengono
Zi(f) = Zu(f) ≃ Z0(f), mentre la (
21.166) si semplifica in
Hq(f) = 2 e− dγ(f); nel caso generale risulta pertanto
Gd(f) = |Hq(f)|2 ⋅ |Hi(f)|2 ⋅ Rg(f)Ru(f) = 4 ⋅ e− 2dα(f) ⋅ |Hi(f)|2 ⋅ Rg(f)Ru(f)
che evidenzia due cause di distorsione lineare, ossia quella intrinseca legata ad
α(f), e quella che dipende dal disadattamento di impedenze in ingresso ed uscita. La seconda causa può essere rimossa qualora si realizzi la condizione di adattamento
Zg(f) = Zc(f) = Z0(f), ottenendo (eq.
(21.168))
Ad(f) = 1Gd(f) = e2dα(f)
che circoscrive la causa della distorsione lineare al solo comportamento
non perfetto di
Hq(f) = 2 e− dγ(f), che può essere
neutralizzato solo nel caso in cui le costanti primarie soddisfino le condizioni di Heaviside.
Ma in pratica il risultato è diverso, perché.... le “costanti primarie” non sono costanti !!!
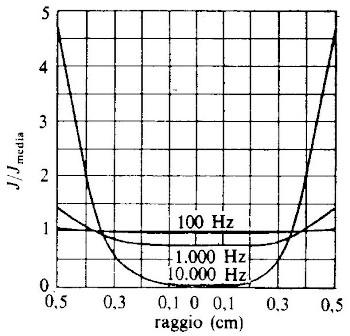
Si tratta di un fenomeno legato all’addensamento del moto degli elettroni presso la superficie del cavo, fenomeno sempre più marcato al crescere della frequenza, come riportato in fig.
19.4.
Per questo motivo la superficie del conduttore realmente attraversata da corrente elettrica è sempre più ridotta all’aumentare di
f, ed a questo corrisponde un aumento della resistenza per unità di lunghezza
r. Si può mostrare che per frequenze maggiori di 50-100 KHz il valore di
r aumenta proporzio- nalmente a
√f, e quindi si può scrivere
α(f) = α0√f, in cui la costante
α0 dipende dal tipo di cavo.
In tali condizioni l’attenuazione disponibile risulta
Ad(f) = e2dα(f) = e2dα0√f, a cui corrisponde un valore in dB pari a
Ad(f)|dB = 10 log10 e2dα0√f = = dα0√f ⋅ 10 log10 e2 = A0 ⋅ d ⋅ √f
Il valore
A0 riassume in se tutte le costanti coinvolte, prende il nome di
attenuazione chilometrica, ed è espresso in dB/Km; il suo valore dipende dal tipo di cavo ed è fornito con riferimento ad una determinata frequenza
fR (ad es. 1 MHz), permettendo di scrivere
in cui
fR rappresenta appunto la frequenza per la quale è disponibile il valore di
A0, ed il valore della
f per cui si calcola
Ad va espresso nella stessa unità di misura di
fR. Questo risultato può essere usato come formula di progetto, e mette in evidenza come l’attenuazione in dB dei cavi sia linearmente proporzionale alla lunghezza.
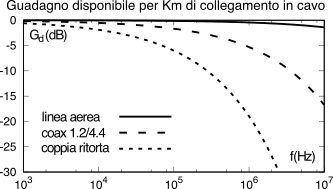
La figura a lato mostra l’andamento di
Gd(f)|dB = − Ad(f)|dB che si ottiene adottando i valori di
A0 e
fR riportati al §
19.2.3 per alcune tipologie di cavo.
In presenza di effetto pelle la funzione di trasferimento intrinseca
Hq(f) = 2 e− dγ(f) presenta una dipendenza da
f tutt’altro che perfetta, causando distorsione lineare sui segnali in transito qualora questi contengano frequenze oltre la banda audio. Un problema analogo insorge anche in assenza di effetto pelle, qualora si manifesti un disadattamento di impedenze ed il cavo non sia sufficientemente lungo (vedi pag.
1).
Se la banda di segnale è sufficientemente estesa da causare una distorsione lineare non trascurabile, o se la particolare natura del segnale (ad es. numerico) richiede la presenza di un ritardo strettamente costante con f, è necessario prevedere uno stadio di equalizzazione. D’altra parte, una volta stimata la H(f) da equalizzare, la natura statica del collegamento permette di evitare tecniche di equalizzazione marcatamente adattative.
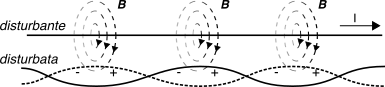
La diafonia, indicata in inglese con il termine di crosstalk, consiste nel fenomeno di interferenza tra segnali che transitano su cavi disposti in prossimità reciproca, e dovuti a fenomeni di induzione elettromagnetica ed accoppiamenti elettrostatici. Il fenomeno è particolarmente rilevante in tutti i casi in cui molti cavi giacciono affasciati in una medesima canalizzazione, condividendo un lunghezza significativa di percorso. Nel caso di telefonia analogica, la diafonia può causare l’ascolto indesiderato di altre comunicazioni; nel caso di trasmissioni numeriche o di segnali modulati, la diafonia produce un disturbo additivo supplementare, che peggiora le prestazioni espresse in termini di probabilità di errore o di SNR.
Con riferimento allo schema della figura soprastante, consideriamo un collegamento tra
D e
C su cui gravano due cause di interferenza: il collegamento da
E ad
F produce il fenomeno di
paradiafonia (in inglese
next,
near end crosstalk), mentre il collegamento da
B ad
A produce il fenomeno di
telediafonia (
fext,
far end crosstalk). Nel primo caso il segnale disturbante ha origine in prossimità del punto di prelievo del segnale disturbato, mentre nel secondo ha origine in prossimità del punto di immissione.
L’entità del disturbo è quantificata mediante un valore di
attenuazione di diafonia tra le sorgenti disturbanti e l’estremo disturbato. La circostanza che, nei rispettivi punti di immissione, i segnali disturbanti hanno la stessa potenza della sorgente che emette il segnale disturbato permette di definire lo
scarto di paradifonia
ΔAEC|dB = AEC|dB − ADC|dB
come la differenza in dB tra l’
attenuazione di paradiafonia AEC|dB e l’
attenuazione del collegamento ADC|dB. Il livello di potenza del segnale disturbante proveniente da
E ed osservato al punto
C risulta quindi pari a
WnextE = WE − AEC = WD − AEC = WC + ADC − AEC = WC − ΔAEC
ossia di
ΔAEC dB inferiore al segnale utile. Una definizione del tutto analoga risulta per la telediafonia (
fext), per la quale il livello di potenza del segnale disturbante proveniente da
B ed osservato al punto
C risulta pari a
WfextB = WC − ΔABC, in cui lo
scarto di telediafonia ΔABC ha il valore
ΔABC|dB = ABC|dB − ADC|dB
Completiamo l’analisi considerando i seguenti due casi particolari.
E’ un modello applicabile per tutte quelle frequenze tali da verificare
r≪2πfl e
g≪2πfc. In tal caso le (
21.162) e (
21.163) forniscono
Z0(f) = R0 = √lc reale e γ(f) = j2πf√lc
Di conseguenza, è facile realizzare
Zg = Zc = R0 in modo da ottenere
Hq(f) = 2 e− jd2πf√lc
e quindi il cavo non presenta distorsione di ampiezza, ha una attenuazione trascurabile, e manifesta una distorsione di fase lineare in
f, realizzando quindi le condizioni di canale perfetto.
E’ il caso di collegamenti interni agli apparati, o tra un trasmettitore-ricevitore e la relativa antenna. La ridotta lunghezza del cavo permette di scrivere
e− dγ(f) = e− dα(f) e− jdβ(f) ≃ e− jdβ(f)
in quanto
e− dα(f) ≃ 1.
Qualora si verifichi un disadattamento di impedenze i coefficienti di riflessione
rg(f) e
rc(f) risultano diversi da zero, rendendo
Hq(f) = 2 e− jdβ(f)1 − rg(f) ⋅ rc(f) ⋅ e −j2dβ(f)
periodica con
d e con
f (quest’ultimo in assenza di effetto pelle). In particolare, se il carico viene sconnesso, o l’uscita del cavo posta in corto circuito, l’eq. (
21.164) mostra come rispettivamente risulti
rc(f) = ±1, per cui la prima delle (
21.165) diviene
Zi(f) = Z0(f) 1± e −j2dβ(f)1∓ e −j2dβ(f)
e pertanto per i valori (ricorrenti) di frequenza
f (o di distanza
d) che rendono
e −j2dβ(f) = ±1 (), l’impedenza di ingresso del cavo può risultare infinita o nulla.
Evidentemente la distorsione lineare prodotta in questo caso ha un andamento del tutto dipendente dalle particolari condizioni operative, e dunque la sua equalizzazione deve prevedere componenti in grado di adattarsi alla Hq(f) del caso. D’altra parte, una volta equalizzato il cavo non sono necessari ulteriori aggiustamenti, a parte problemi di deriva termica. Diverso è il caso dal punto di vista di un terminale di rete, per il quale il cavo effettivamente utilizzato può essere diverso da collegamento a collegamento, e pertanto i dispositivi modem a velocità più elevate devono disporre di un componente di equalizzazione adattiva, da regolare ogni volta ad inizio del collegamento.
19.2.3 Tipologie di cavi per le telecomunicazioni
Descriviamo i principali tipi di cavo utilizzati, per i quali forniamo in tabella i valori tipici delle grandezze essenziali, nelle condizioni illustrate nel testo che segue.
19.2.3.1 Coppia simmetrica
In questo caso il cavo è costituito da due conduttori uguali, la distanza tra i quali permette di definire due sottoclassi: linea aerea e coppia ritorta.
Si tratta di conduttori nudi, di bronzo od acciaio rivestito in rame, con diametro
φ da 2 a 4 mm, sostenuti da una palificazione che li mantiene a distanza di 15 - 30 cm. L’uso delle linee aeree è andato estinguendosi con il tempo, ma rimane largamente diffuso nei paesi meno sviluppati.
I valori riportati in tabella sono riferiti a conduttori con φ = 3 mm, a frequenza di 1 KHz; la r già a 100 KHz cresce al valore di 20 Ω/Km, mentre la conduttanza g a 100 KHz e con tempo molto umido, può crescere fino a decine di volte il suo valore nominale ad 1 KHz. I valori riportati mostrano come le condizioni di Heaviside non siano rispettate, in quanto rc ≫ lg, anche se lo scarto è inferiore rispetto al caso delle coppie ritorte.
L’impedenza caratteristica riportata in tabella, di circa 600 Ω, è ottenuta applicando il modello a basse perdite, con le costanti primarie indicate.
E’ costituita da una coppia di conduttori in rame con
φ da 0.4 ad 1.3 mm, rivestiti di materiale isolante, ed avvolti tra loro secondo
eliche con passo grande rispetto al diametro. Un numero variabile di tali coppie (tra qualche decina e qualche centinaio) sono poi raggruppate assieme, e rivestite con guaine protettive isolanti o metalliche; il risultato dell’operazione è interrato o sospeso mediante una fune in acciaio. L’uso delle coppie ritorte, nato allo scopo di realizzare il collegamento tra utente e centrale telefonica, si è esteso al cablaggio di reti locali (
lan) con topologia a stella (
ieee 802.3); in tale contesto i cavi sono indicati come
utp (
unshielded twisted pair).
I valori riportati in tabella sono riferiti a conduttori con
φ = .7 mm a frequenza di 1 KHz; la
r a 100 KHz è circa doppia. La
g dipende sostanzialmente dall’isolante utilizzato, mentre l’aumento di
c è evidentemente legato alla vicinanza dei conduttori. Anche in questo caso risulta
rc ≫ lg, e dunque le condizioni di Heaviside non sono verificate. Nel passato si è fatto largo uso dell’espediente di innalzare artificialmente
l, collocando ad intervalli regolari una induttanza “concentrata” (le cosiddette bobine
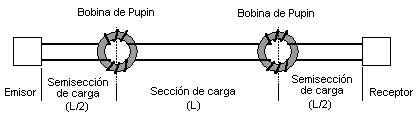
Pupin), realizzando così nella banda del canale telefonico un comportamento approssimativamente perfetto. Ma al crescere della frequenza le bobine
Pupin producono un effetto passa basso, aumentando di molto il valore di attenuazione. In tempi successivi, quando le stesse coppie ritorte sono state utilizzate per la trasmissione di segnali numerici PCM, le bobine Pupin sono state rimosse, ed al loro posto inseriti ripetitori rigenerativi (§
18.3.2). L’impedenza caratteristica di circa 600
Ω riportata nella tabella di pag.
1 è quella valida a frequenze audio, con cavi di diametro
φ = .7 mm. Prevalendo l’aspetto capacitivo, al crescere della frequenza
Z0 si riduce a 100-200
Ω, con fase di -10 gradi. L’attenuazione chilometrica riportata è sempre relativa al caso
φ = .7 mm; per diametri di 1.3 mm si ottengono valori circa dimezzati, mentre con
φ = .4 mm il valore di
A0 risulta maggiore.
La configurazione a spirale dei conduttori ha infine lo scopo di ridurre i fenomeni di diafonia tra circuiti differenti. Infatti se il passo dell’elica è diverso tra le coppie affasciate in unico cavo, le tensioni e correnti indotte da una coppia su di un’altra non interessano sempre lo stesso conduttore, ma entrambi in modo alternato. L’avvolgimento della coppia disturbante produce inoltre una alternanza dei conduttori in vicinanza della coppia disturbata, aggiungendo una ulteriore alternanza del verso del fenomeno di disturbo. Con questi accorgimenti si trovano attenuazioni di diafonia a frequenze vocali dell’ordine di 80-90 dB su 6 Km. All’aumentare della frequenza, e della lunghezza del percorso comune, l’attenuazione di diafonia diminuisce (e quindi l’interferenza aumenta), fino a mostrare valori di 60-70 dB a 750 KHz su 1.6 Km.
In questo caso è presente un conduttore centrale ricoperto di dielettrico, su cui è avvolto il secondo conduttore, intrecciato a formare una sorta di
calza, connesso
a massa ad entrambe le estremità, e racchiuso a sua volta in una guaina isolante. La particolare conformazione del cavo lo rende molto più resistente ai fenomeni di interferenza, svolgendo una funzione di
gabbia di Faraday.
Indicando con
φ il diametro del conduttore interno e con
D quello esterno, la teoria mostra che si determina un minimo di attenuazione se
D ⁄ φ = 3.6; per questo sono stati normalizzati i diametri mostrati nella tabella a pag.
1. Il tipo con
φ ⁄ D = 8.4 ⁄ 38 mm è sottomarino, e presenta la minima attenuazione chilometrica;
A0 aumenta al diminuire della sezione del cavo. Finché
D ⁄ φ = 3.6, l’impedenza caratteristica dipende solo dal dielettrico, con l’espressione generale fornita in tabella, ottenendo i valori di 50 e 75
Ω con dielettrico aria e polietilene rispettivamente. I valori delle costanti primarie riportati in tabella sono ottenuti facendo uso delle relazioni
r = 8.4 ⋅ 10−8√f⎛⎝1D + 1φ⎞⎠ Ωm l = 0.46 log10 Dφ μHm
g = 152 ⋅ 10−12 fεrtanδlog10Dφ Sm c = 24.2 ⋅ εrlog10 Dφ pFm
in cui si è posto f (in Hz nelle formule) pari a 1 MHz, D e d sono espressi in metri, εr è la costante dielettrica, e tanδ è l’angolo di perdita del dielettrico; nel caso del polietilene, risulta εr = 2.3, tanδ = 3 ⋅ 10 − 4.
Esercizio Si desidera effettuare una trasmissione FDM di 120 canali telefonici, ognuno modulato AM-BLU, su di un cavo coassiale, nella banda di frequenze 1÷1.48 MHz. Desiderando una potenza ricevuta per ogni canale di almeno 1 mW, e disponendo di un trasmettitore in grado di erogare 10 W, determinare la massima lunghezza del collegamento, supponendo verificate le condizioni di adattamento agli estremi del cavo, con impedenza caratteristica resistiva, ed attenuazione chilometrica A0 = 5.3 dB/Km ad 1MHz. Di quanto dovrebbe aumentare la potenza trasmessa WdT per raddoppiare la lunghezza?
Soluzione Supponendo tutti i canali contemporaneamente attivi, la potenza trasmessa per ciascuno di essi risulta pari a
-
W(n)dT = 10120 = 83.3 mW, con n = 1, 2, …, 120.
Tra tutti i canali, quello che subisce la massima attenuazione chilometrica è quello con portante più elevata, per il quale
A(120)d (dB/Km) = A0√1.48 = 5.3 ⋅ 1.22 = 6.46 dB/Km.
Per questo canale il guadagno di sistema risulta pari a
G(120)s|dB = 10log10W(120)dTWRMin = 10log1083.31 = 19.2
dB,
essendo WRMin = 1 mW come indicato nel testo. Come noto, Gs corrisponde alla massima attenuazione AdTot che può essere accettata, e pertanto
A(120)dTot|dB = A(120)d(dB ⁄ Km) ⋅ LKm = 19.2
dB,
da cui si ricava per la massima lunghezza
LKm = A(120)dTot|dBA(120)d(dB ⁄ Km) = 19.26.46 = 2.97 Km,
che come vediamo è imposta dal canale più attenuato. Per il primo canale si ha invece A(1)d(dB ⁄ Km) = A0, e dunque
A(1)dTot|dB = A0(dB ⁄ Km) ⋅ LKm = 5.3 ⋅ 2.97 = 15.74 dB.
La differenza tra Gs|dB (uguale per tutti i canali) e A(1)dTot|dB rappresenta il margine di sistema per il primo canale, pari a
M = Gs − Ad = 19.2 − 15.74 = 3.46 dB.
La stessa quantità è anche una misura della distorsione lineare di ampiezza del cavo nella banda del segnale.
Nel caso si voglia superare una lunghezza doppia anche A(120)dTot|dB raddoppia, e per mantenere WRMin = 1 mW deve raddoppiare anche G(120)s|dB. Pertanto la nuova potenza/canale risulta
W’dT(dBm) = WRmin(dBm) + G’s(dB) = 0 + 2Gs(dB)
quindi
W’dT(mW) = 10W’dT(dBm)10 = 102Gs(dB)10 = 102 ⋅ 19.210 = 103.84 = 6918.3 milliWatt,
cioè 6.91 Watt/canale, e quindi 6.91 ⋅ 120 = 830 Watt complessivi !