Potenza assorbita da un bipolo, potenza disponibile e adattamento di impedenza, guadagno disponibile

Prev Capitolo 18: Caratterizzazione circuitale, rumore ed equalizzazione dati Su Capitolo 18: Caratterizzazione circuitale, rumore ed equalizzazione dati Sezione 18.2: Rumore nelle reti due porte Next

18.1 Modello circuitale dei segnali

Fino ad ora un segnale è stato trattato nelle diverse forme di espressione analitica, sequenza simbolica, grandezza aleatoria, forma d’onda nel tempo, e densità spettrale. E’ giunto il tempo di confrontarci con la corrispettiva grandezza elettrica (o elettromagnetica) che lo veicola.

Potenza di segnale e grandezze elettriche

La caratterizzazione energetica dei segnali si è finora svolta a prescindere dalla natura fisica degli stessi, in quanto non è mai stato specificato se si trattasse di tensioni o correnti, né si sono indicate le impedenze in gioco. Trattando ora di grandezze elettriche le potenze di segnale, di tensione o di corrente, saranno misurate in (Volt)² o in (Ampere)² rispettivamente.

Esempio Sia x(t) un segnale di tensione. La sua potenza P_x ha unità di misura [V²], mentre la relativa densità di potenza P_x(f) si esprime in [^V²⁄_Hz].

Eseguiamo quindi una distinzione relativa al ruolo che il circuito ha nei confronti del segnale, tradizionalmente basata sul numero di porte del circuito.

Numero di porte

Le coppie di morsetti a cui applicare o da cui prelevare un segnale vengono denominate porte. In questo senso un generatore che appunto produce il segnale, ed una impedenza di carico che ne assorbe la potenza, costituiscono reti ad una porta. Al contrario, l’oggetto che abbiamo fin qui indicato come filtro, o canale, da un punto di vista circuitale è un sistema fisico dotato di una relazione ingresso-uscita, e per questo indicato come rete due porte.

Modello di rappresentazione

Un circuito può essere rappresentato mediante il suo modello circuitale,

in cui sono evidenziati generatori, resistenze, impedenze, generatori controllati..., oppure il suo schema simbolico, in cui sono mostrate solamente le relazioni funzionali tra i segnali in transito.

Proprietà delle reti due porte

Le proprietà di linearità, permanenza, realizzabilità ideale e fisica, stabilità, già definite al § 1.6 per i sistemi fisici, possono essere verificate o meno nelle reti due porte. D’altra parte, alcune relazioni e grandezze che nella teoria dei circuiti sono definite per segnali puramente sinusoidali, come per la corrente alternata, nella teoria dei segnali devono essere ridefinite in modo da tenere nel giusto conto dell’intera densità spettrale dei segnali con un contenuto informativo.

18.1.1 Bipoli

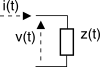
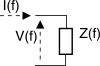
Distinguiamo tra quelli tipo attivo o di tipo passivo.

Passivi

Non contengono generatori, e sono caratterizzati dalle relazioni esistenti tra la tensione ai loro capi e la corrente che vi scorre (entrante). Il legame tra le due grandezze è una convoluzione

v(t) = i(t) * z(t)

in cui si suppone i(t) la causa e v(t) l’effetto. La trasformata di Fourier fornisce V(f) = I(f) ⋅ Z(f) in cui Z(f) prende il nome di impedenza, e può scriversi nei termini di parte reale ed immaginaria:

Z(f) = R(f) + jX(f)

in cui R(f) (resistenza) è una funzione pari di f (e sempre positiva), mentre X(f) (reattanza) è dispari: pertanto, Z(f) = Z^*(−f) e quindi z(t) è reale. Allo stesso tempo è definita l’ammettenza

Y(f) = 1Z(f) = 1R(f) + jX(f) = R(f) − jX(f)|Z(f)|²

e la corrispondente y(t) = F ⁻¹{Y(f)}, permettendo di scrivere i(t) = v(t) * y(t), in cui il ruolo di causa ed effetto per i(t) e v(t) è invertito.

Attivi

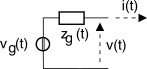
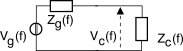
Sono bipoli al cui interno è presente un generatore. Per il teorema di Thévenin, [1013] [1013] Vedi ad es. http://it.wikipedia.org/wiki/Teorema_di_Thévenin qualunque circuito può essere ridotto ad un generatore di tensione con in serie una impedenza (vedi figura), in cui V_g(f) rappresenta la tensione a vuoto, ossia quando I(f) = 0 (considerata uscente nei bipoli attivi).

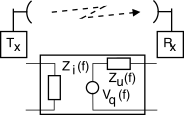
Esempio Una antenna trasmittente (§ 20.1)

è schematizzabile come un bipolo passivo di impedenza pari all’impedenza di ingresso dell’antenna che assorbe la potenza erogata dal trasmettitore. Una antenna ricevente è schematizzabile come un generatore di tensione con in serie la propria impedenza di uscita, e trasferisce allo stadio di ingresso del ricevitore la potenza ricevuta per via elettromagnetica.

18.1.1.1 Potenza assorbita da un bipolo

Se ad un bipolo passivo di impedenza Z(f) è applicato un segnale di tensione con spettro di densità di potenza P_v(f) la potenza dissipata sul bipolo (o assorbita), indicata come W_z per distinguerla da quella di segnale P_v, ha densità

(21.122)
W_z(f) = P_v(f) ⋅ ℜ{Y(f)} = P_v(f)R(f)|Z(f)|² ⎡⎣V²Ω ⋅ Hz⎤⎦ = ⎡⎣WattHz⎤⎦

La dimostrazione di tale relazione è fornita al § 18.5.1. Osserviamo come la dipendenza di Y(f) dalla frequenza svolga una azione filtrante, e la potenza totale assorbita (o dissipata) su Z(f) vale

W_z = ^∞⌠⌡_−∞P_v(f)R(f)|Z(f)|² df [Watt]

18.1.1.2 Connessione tra generatore e carico

La tensione ai capi del carico è valutabile applicando la regola del partitore [1014] [1014] http://it.wikipedia.org/wiki/Partitore_di_tensione:

V_c(f) = V_g(f) Z_c(f)Z_c(f) + Z_g(f)

ossia V_c(f) = V_g(f)H(f) con H(f) = Z_c(f)Z_c(f) + Z_g(f). La densità di potenza di segnale ai capi del carico vale quindi P_{v_c}(f) = P_{v_g}(f)|H(f)|², e la densità di potenza dissipata su Z_c(f) risulta

(21.123)
W_{z_c}(f) = P_{v_c}(f) R_c(f)|Z_c(f)|² = P_{v_g}(f)||Z_c(f)Z_c(f) + Z_g(f)||²R_c(f)|Z_c(f)|² = = P_{v_g}(f) R_c(f)|Z_c(f) + Z_g(f)|²

Osserviamo dunque che la densità di potenza assorbita dal carico dipende da Z_c(f), che compare sia a denominatore che a numeratore con R_c(f). Ci chiediamo allora quale sia il valore di Z_c che realizza il massimo trasferimento di potenza tra generatore e carico, sfruttando così appieno la potenzialità del generatore, indicata come potenza disponibile.

18.1.1.3 Potenza disponibile e massimo trasferimento di potenza

La W_{z_c}(f) espressa da (21.123) risulta massima quando il denominatore viene reso minimo, ed al § 18.5.2 si mostra che ciò avviene qualora risulti R_c(f) = R_g(f) e X_c(f) = − X_g(f), ovvero Z_c(f) = Z^*_g(f), in modo da poter enunciare

(21.124) se Z_c(f) = Z^*_g(f) allora W_{z_c}(f) = max_{Z_c(f)}{W_{z_c}(f)} = P_{v_g}(f)4R_g(f) = W_{d_g}(f)

Il valore W_{d_g}(f) = P_{v_g}(f)4R_g(f) prende il nome di spettro di potenza disponibile del generatore, dipende solo dai suoi parametri P_{v_g}(f) e R_g(f), e rappresenta la massima potenza ceduta ad un carico che è adattato per il massimo trasferimento di potenza [1015] [1015] E’ bene notare esplicitamente che questo massimo è valido solo nel caso in cui non sia possibile modificare la Z_g(f). Altrimenti, per un qualunque valore fissato di Z_c(f), il massimo di W_{z_c}(f) si ottiene quando Z_g(f) → 0..

La potenza disponibile W_{d_g}(f) è pertanto una grandezza caratteristica del generatore; la potenza effettivamente ceduta ad un carico generico Z_c(f) ≠ Z^*_g(f), risulta inferiore a W_{d_g}(f) di una quantità

α(f) = 4R_g(f)R_c(f)|Z_g(f) + Z_c(f)|²

(vedi § 18.5.3) e quindi in generale si ha W_{z_c}(f) = α(f) W_{d_g}(f).

18.1.1.4 Adattamento di impedenza per assenza di distorsione lineare

Abbiamo già osservato come la tensione ai capi del carico abbia valore V_c(f) = V_g(f) ⋅ Z_c(f)Z_c(f) + Z_g(f) = V_g(f) H(f). Ci chiediamo ora quali condizioni debbano sussistere affinché H(f) si comporti come un canale perfetto (pag. 1), ovvero risulti |H(f)| = cost e arg{H(f)} = − 2πfτ: tali condizioni sono anche indicate come assenza di distorsione lineare. Il risultato cercato si ottiene qualora si ponga

Z_c(f) = α Z_g(f) con α reale

infatti in tal caso risulta

H(f) = α Z_g(f)(1 + α) Z_g(f) = α1 + α

ossia H(f) costante. La condizione Z_c(f) = αZ_g(f) prende il nome di adattamento di impedenza, a volte ristretta al caso in cui α = 1.

Z_g(f) reale

Notiamo che massimo trasferimento di potenza ed assenza di distorsione lineare possono sussistere congiuntamente, a patto che Z_g(f) = R_g, ovvero quando sia il generatore che il carico sono caratterizzati da una impedenza reale.

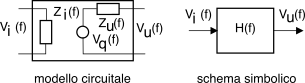
18.1.2 Reti due porte

Come anticipato un circuito accessibile mediante due coppie di morsetti è detto rete due porte, e può essere rappresentata secondo almeno due diversi formalismi: il modello circuitale e lo schema simbolico.

18.1.2.1 Modello circuitale

In figura è mostrato un possibile modello circuitale [1016] [1016]

Sono chiaramente possibili modelli diversi, basati su topologie e relazioni differenti. Esistono infatti circuiti a T, ad L, a scala, a traliccio, a pigreco; le relazioni tra le grandezze di ingresso ed uscita possono essere espresse mediante modelli definiti in termini di impedenze, ammettenze, e parametri ibridi.
Il caso qui trattato è quello di un modello ibrido, con la particolarità di non presentare influenze esplicite dell’uscita sull’ingresso. Qualora il circuito che si descrive presenti una dipendenza, ad esempio di Z_i da Z_c, o Z_u da Z_g, questo deve risultare nell’espressione della grandezza dipendente. Viceversa, qualora il circuito presenti in ingresso un generatore controllato da una grandezza di uscita, il modello non è più applicabile.

per una rete due porte,

caratterizzata in termini di impedenza di ingresso Z_i(f), di uscita Z_u(f), e di un generatore controllato con tensione a vuoto

V_q(f) = H_q(f) V_i(f)

Le condizioni di chiusura sono quelle di un generatore V_g(f) con impedenza Z_g(f) in ingresso, e di una impedenza di carico Z_c(f) in uscita.

La tensione V_i(f) all’ingresso della rete

V_i(f) = V_g(f) H_i(f)

dipende da quella del generatore V_g(f) mediante il rapporto di partizione H_i(f) = Z_i(f)Z_g(f) + Z_i(f), così come la tensione in uscita

V_u(f) = V_q(f) H_u(f)

dipende da quella del generatore controllato V_q(f) mediante il rapporto di partizione H_u(f) = Z_c(f)Z_u(f) + Z_c(f). Combinando queste relazioni, si ottiene che la risposta in frequenza complessiva H(f) risulta:

(21.125)
V_u(f) = V_g(f) H_i(f) H_q(f) H_u(f) = V_g(f) H(f)

La relazione mostra come H(f) dipenda, oltre che dalla risposta in frequenza intrinseca della rete H_q(f), anche dalle condizioni di adattamento che si realizzano in ingresso ed in uscita.

18.1.2.2 Schema simbolico

Lo stesso modello circuitale descritto può essere rappresentato equivalentemente mediante lo schema simbolico

rappresentato a lato, in cui sono evidenziate le tre funzioni di trasferimento sopra ricavate, e che operano sui segnali indicati. Lo schema simbolico ha il vantaggio di trascendere dal modello circuitale soggiacente, e di rendere del tutto evidente come la risposta in frequenza complessiva abbia origine dal prodotto di tre termini, di cui solo uno (H_q(f)) rappresenta la rete due porte in senso stretto.

18.1.2.3 Trasferimento energetico

Applicando ora la (21.122) alla potenza ceduta dal generatore controllato V_q(f) al carico Z_c(f), e tenendo conto della (21.125), si ottiene

W_c(f) = P_{v_u}(f) R_c(f)|Z_c(f)|² = P_{v_g}(f) |H(f)|² R_c(f)|Z_c(f)|²

che dipende anche da Z_c(f). Proseguiamo l’analisi nel tentativo di individuare una relazione di trasferimento energetico che rappresenti caratteristiche della sola rete.

Guadagno di tensione

E’ definito come il rapporto tra tensione di uscita e di ingresso:

G_v(f) = V_u(f)V_i(f) = H_q(f) H_u(f)

Evidentemente, dipende dalle condizioni di chiusura all’uscita della rete.

Guadagno di potenza

E’ il rapporto tra la potenza ceduta al carico e quella assorbita all’ingresso della rete:

G_W(f) = W_c(f)W_i(f) = P_{v_g}(f) |H(f)|² R_c(f)|Z_c(f)|² ⋅ 1 P_{v_g}(f) |Z_g(f) + Z_i(f)|²R_i(f) = = |H(f)|² R_c(f)R_i(f) ⋅ ||Z_g(f) + Z_i(f)Z_c(f)||² = = |H_q(f)|² ⋅ R_c(f)R_i(f) ⋅ ||Z_i(f)Z_u(f) + Z_c(f)||²

ed evidentemente è ancora funzione di Z_c(f) ( [1017] [1017] L’ultimo passaggio tiene conto che (omettendo la dipendenza da f):

|H|² ⋅ ||Z_g + Z_iZ_c||² = ||Z_iZ_i + Z_gH_qZ_cZ_c + Z_u||²||Z_g + Z_iZ_c||² = |H_q|² ⋅ ||Z_iZ_u + Z_c||²

). Notiamo ora che, qualora il carico sia adattato per il massimo trasferimento di potenza (Z_c(f) = Z^*_u(f)), la potenza ceduta a Z_c(f) (e quindi G_W(f)) è massima, e la dipendenza di G_W(f) da Z_c(f) decade, risultando

(21.126)
G_{W_Max}(f) = |H_q(f)|² ⋅ |Z_i(f)|²4R_i(f)R_u(f)

Guadagno disponibile

Il rapporto tra la potenza disponibile di uscita e quella disponibile del generatore posto in ingresso della rete, indipendentemente dal fatto se l’ingresso della rete presenti o meno le condizioni per il massimo trasferimento di potenza, è detto guadagno disponibile e vale

(21.127)
G_d(f) = W_{d_u}(f)W_{d_g}(f) = P_{v_q}(f)4R_u(f) ⋅ 4R_g(f)P_{v_g}(f) = = P_{v_g}(f) |H_i(f)|² |H_q(f)|² ⋅ R_g(f)R_u(f) ⋅ 1 P_{v_g}(f) = = |H_i(f)|² |H_q(f)|² ⋅ R_g(f)R_u(f)

La relazione trovata mostra la dipendenza di G_d(f) dalle condizioni di chiusura in ingresso. Quando l’impedenza di ingresso Z_i(f) è tale da permettere il conseguimento del massimo trasferimento di potenza, ovvero Z_g(f) = Z^*_i(f), la dipendenza decade ed |H_i(f)|² = ||Z_i(f)Z_i(f) + Z^*_i(f)||² = |Z_i(f)|²4R²_i(f); considerando inoltre che R_g(f) = R_i(f), la (21.127) diviene

(21.128)
G_{d_Max}(f) = |H_q(f)|² ⋅ |Z_i(f)|²4R_u(f)R_i(f)

Quest’ultima quantità è chiamata guadagno disponibile della rete due porte ed è quella che appunto dipende solo dai parametri della rete stessa. Confrontando (21.128) con (21.126) notiamo che G_{d_Max}(f) coincide con G_{W_Max}(f). Confrontando (21.128) con (21.127), troviamo che G_d(f) = |H_i(f)|² G_{d_Max}(f) 4R_g(f)R_i(f)|Z_i(f)|². Considerando ora che

|H_i(f)|²1|Z_i(f)|² = ||Z_i(f)Z_i(f) + Z_g(f)||²1|Z_i(f)|² = 1|Z_i(f) + Z_g(f)|²

, otteniamo

G_d(f) = 4R_g(f)R_i(f)|Z_g(f) + Z_i(f)|² ⋅ G_{d_Max}(f)

che ci consente di valutare G_d(f) nelle reali condizioni di chiusura in ingresso, a partire da G_{d_Max}(f) = G_{W_Max}(f) che dipende solo dalla rete.

Collegamento generatore-carico mediante rete due porte

Considerando generatore e porta di ingresso della rete adattati per il massimo trasferimento di potenza, la densità di potenza disponibile in uscita risulta
W_{d_u}(f) = G_{d_Max}(f) W_{d_g}(f)
e dunque l’uscita della rete due porte si comporta come un generatore equivalente, caratterizzato da una nuova W_{d_u}(f) ed una diversa impedenza interna Z_u(f);
se in ingresso non si verifica massimo trasferimento di potenza G_d(f) si riduce di un fattore β(f) = 4R_g(f)R_i(f)|Z_g(f) + Z_i(f)|², e dunque la nuova potenza disponibile in uscita risulta
W_{d_u}(f) = β(f) ⋅ G_{d_Max}(f) W_{d_g}(f) = 4R_g(f)R_i(f)|Z_g(f) + Z_i(f)|² ⋅ G_{d_Max}(f) W_{d_g}(f)
se infine il carico Z_c(f) in uscita alla rete non è adattato, assorbe una potenza inferiore a W_{d_u}(f) e pari a (vedi Appendice 18.5.3)
W_c(f) = α(f) ⋅ W_{d_u}(f) = 4R_u(f)R_c(f)|Z_u(f) + Z_c(f)|² ⋅ W_{d_u}(f)

Reti passive

Se una rete non contiene elementi attivi allora G_{d_Max}(f) ≤ 1 per qualunque f. In questo caso si parla più propriamente di attenuazione disponibile A_d(f) = 1G_d(f) ovvero A_d(f) [dB] = − G_d(f) [dB].

Reti in cascata

Se più reti sono connesse tra loro l’una di seguito all’altra, e si verificano per ciascuna coppia le condizioni di massimo trasferimento di potenza tra lo stadio di uscita di una e quello di ingresso della successiva, il guadagno disponibile complessivo è il prodotto dei singoli guadagni disponibili: G_{d_Tot} = G_d1 ⋅ G_d2 ⋅ … ⋅G_dN.

Esempio In figura è mostrato un generatore con potenza disponibile W_dg collegato ad una serie di tre reti due porte; l’effetto complessivo è quello di un nuovo generatore

di uscita con potenza disponibile W_du pari al prodotto di quella del generatore originario, moltiplicata per i guadagni disponibili delle reti attraversate, tenendo anche eventualmente conto delle attenuazioni supplementari [1018] [1018] L’attenuazione supplementare (pag. 1) può esprimere il peggioramento dovuto al mancato verificarsi delle condizioni di massimo trasferimento tra le impedenze di uscita e di ingresso delle reti affacciate.:

W_du = W_dg ⋅ G_d1 ⋅ G_d2 ⋅ 1A_d ⋅ 1A_s

che può essere egualmente valutato operando in decibel, come

W_du[dBW] = W_dg[dBW] + G_d1[dB] + G_d2[dB] − A_d[dB] − A_s[dB]

in cui ovviamente, qualora W_dg fosse espresso in dBm anziché dBW, lo stesso accadrebbe per W_du.

Collegamento radio

Con riferimento al circuito equivalente per una coppia di antenne di pag. 1, precisiamo che la potenza trasmessa è quella assorbita dall’impedenza di ingresso dell’antenna trasmittente, mentre quella ricevuta è quella ceduta dal generatore equivalente dell’antenna ricevente, all’impedenza di ingresso del ricevitore.