10.2 Codifica di immagine
Un segnale di immagine può essere di natura
vettoriale, come nel caso di un disegno prodotto da un
plotter, e rappresentato mediante un linguaggio descrittivo che codifica le operazioni grafiche necessarie alla sua realizzazione; al contrario, un segnale di immagine è detto di tipo
bitmap, o
raster (griglia, reticolo), quando è il risultato di un campionamento spaziale
, come nel caso di una foto digitale, di un fax, o del risultato di un processo di scansionamento ottico. Mentre le immagini vettoriali sono pienamente
scalabili e ridimensionabili senza perdita di definizione, quelle bitmap sono ottimizzate per essere riprodotte nelle loro dimensioni originali, avendo già operato un processo di distorsione tale da sfruttare al più possibile le caratteristiche di predicibilità e di sensibilità percettiva.
Per quanto riguarda le immagini bitmap, queste sono definite nei termini di una matrice di elementi di immagine o
pixel (
picture elements), che sono l’equivalente bidimensionale dei campioni estratti da un segnale unidimensionale. Per ogni pixel è definito un valore associato alla intensità con la quale deve essere riprodotto: nel caso di immagini a colori
, sono necessari tre valori di intensità, per cui una immagine è in realtà descritta da tre matrici, come approfondiamo di seguito.
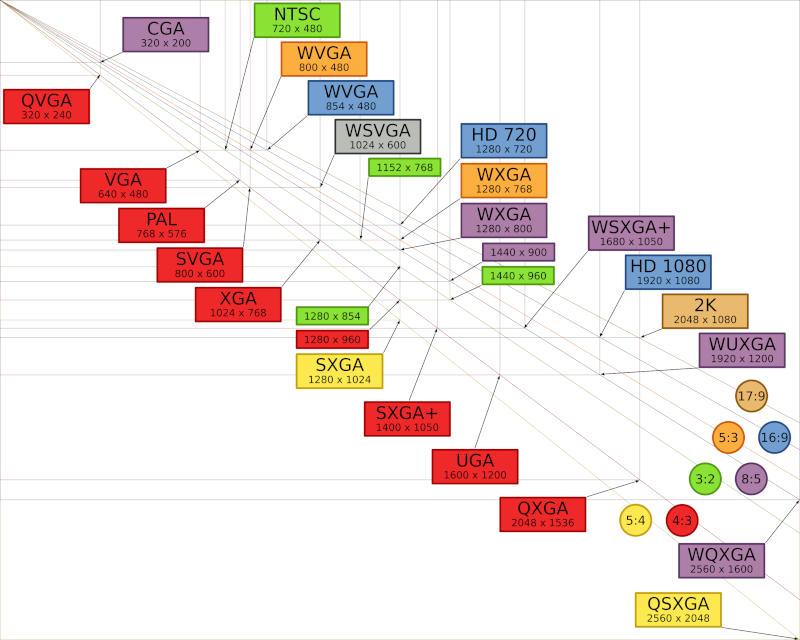
Sebbene le dimensioni della matrice di pixel possano essere qualunque, nel corso del tempo si sono affermati una serie di valori di riferimento, associati ad altrettante sigle, legate al tipo di dispositivo che deve poi riprodurre l’immagine, ma anche a quello da cui l’immagine viene acquisita; la tabella
10.1 riassume tali corrispondenze.
Table 10.1 Griglia dei parametri corrispondenti ai formati video
Ad esempio, la risoluzione
vga (640 x 480) trae origine dai parametri dello standard
ntsc della televisione analogica (§
25.1), i cui quadri sono composti da una serie di 525 linee, di cui solo 480 visibili: volendo mantenere una risoluzione orizzontale pari a quella verticale, con un rapporto d’aspetto di 4:3, ogni linea deve essere campionata su 480/3x4 = 640 punti. Già prima dell’uso broadcast della TV digitale, la raccomandazione BT 601 ha stabilito le regole per la conversione tra standard video differenti, mediante l’uso di una comune frequenza di campionamento del segnale video a 13.5 MHz, individuando così nei 52
μsec () di una linea, un numero di 52 x 10
− 6x 13.5 x 10
6 = 702 campioni per linea, a cui si aggiungono 9 campioni neri in testa ed in coda per ottenere 720 campioni per linea; per un segnale a 525 linee si ottiene quindi la matrice 720 x 480 del formato 4:2:2, che approfondiremo tra breve.
Le matrici più grandi di 1024 x 768 sono spesso descritte in termini di
Megapixel (es 1600 x 1200 = 1,9 Mpixel), spesso usati per confrontare la risoluzione (ma non necessariamente la qualità) dei mezzi di fotografia digitale; inoltre, i
grandi formati traggono origine anche dalla tecnologia delle schede video per computer da un lato, e da quella della televisione ad alta definizione da un altro, come riassunto nella figura
10.26.
Il formato sif (source intermediate format) è ottenuto a partire dal 4:2:2, conservando la metà dei pixel sia in verticale che in orizzontale, e trascurando la metà dei quadri di immagine; il suo uso è orientato alla memorizzazione, e quindi usa una scansione non interallacciata. Il formato cif (common intermediate format) è simile al sif, tranne per aver perso il riferimento al numero di linee analogiche da cui deriva; il suo uso è orientato ai sistemi di videoconferenza, e da questo sono definiti formati a maggior risoluzione, come il 4cif ed il 16cif, equivalenti al 4:2:2 ed all’hdtv. Il formato qcif (quarter cif) è orientato alla videotelefonia, dimezzando ancora sia la risoluzione spaziale che quella temporale. Da questo è a sua volta derivato il formato sub-qcif (o s-qcif) di 128 x 96 pixel, orientato a collegamenti lenti come quelli via modem.
10.2.2 Spazio dei colori
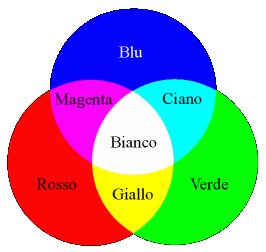
I dispositivi di acquisizione e riproduzione di immagini a colori operano su tre diverse matrici di pixel, che rappresentano i tre colori di base della
sintesi additiva, ossia
rosso,
verde, e
blu, o
rgb (dalle iniziali inglesi
Red,
Green e
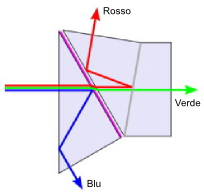
Blue). In figura
10.27 viene mostrato il principio di funzionamento di un
prisma dicroico,
che devia le tre componenti di colore verso tre diversi dispositivi di acquisizione. Variando quindi la proporzione con cui si sommano gli stimoli dei tre colori, si ottiene, oltre al bianco, anche qualunque altro colore. Sebbene dalle figure riportate sembra che il bianco risulti dal contributo in parti uguali delle tre componenti
rgb, in realtà la scala di grigi della immagine
monocromatica corrispondente si ottiene calcolando un segnale
Y di
luminanza secondo la formula
che è quella usata per modulare il segnale video analogico. Come già discusso, in tale ambito la componente di colore viene trasmessa utilizzando due altri segnali,
Cb o
crominanza blu e
Cr o
crominanza rossa, secondo la formula
Disponendo dei segnali
Y,
Cb e
Cr, si possono riottenere i valori
rgb inserendo la (
10.267) nelle (
10.268), e risolvendo il sistema di tre equazioni in tre incognite risultante.
Al §
25.1 abbiamo descritto come nel segnale televisivo analogico la componente di colore sia trasmessa assieme alla luminanza, su di una diversa portante, con modulazione di ampiezza in fase e quadratura. In realtà, per diversi motivi le componenti trasmesse non sono direttamente quelle individuate dalle (
10.268), ma piuttosto componenti denominate
U,
V oppure
I,
Q, e così definite:
PAL: U = 0.493 ⋅ Cb NTSC: I = 0.74 ⋅ Cr − 0.27 ⋅ Cb V = 0.877 ⋅ Cr Q = 0.48 ⋅ Cr + 0.41 ⋅ Cb
Pertanto, in funzione delle diverse modalità di rappresentazione, un segnale video a colori può essere descritto indifferentemente da una delle seguenti quattro terne di segnali:
rgb, ycrcb, yuv, yiq.
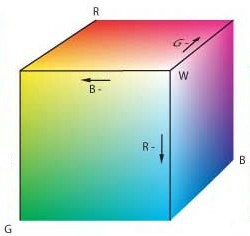
Una descrizione alternativa dello spazio di colore è fornita dai parametri di tinta, saturazione e luminosità, ovvero hue, saturation e lightness, o hsl: si tratta di attributi legati più alla descrizione percettiva che non alle tecnologie della riproduzione dell’immagine. Mentre la tinta descrive una famiglia di colori (es tutti i rossi), la saturazione ne indica il grado di purezza, ossia la presenza congiunta di altre tonalità; la chiarezza, infine, denota la luminosità del colore, rispetto ad un punto bianco. La terna hsl viene a volte usata per descrivere un colore nell’ambito di programmi di computer graphic, mediante i quali è fornito anche l’equivalente rgb.
Dato che l’occhio umano non distingue più di 250 tinte diverse, e di 100 livelli di saturazione, si ritiene che utilizzare 8 bit per ogni componente dello spazio di colore rgb sia più che sufficiente. Con 8x3=24 bit per pixel (bpp) si possono infatti rappresentare 224 − 1 diversi colori, ovvero più di 16 milioni, molti dei quali indistinguibili ad occhio nudo. Modalità più spinte di quella a 24 bpp (detta truecolor) adottano 10, 12, 16 bit/componente, o rappresentazioni in virgola mobile, e sebbene non migliorino la qualità visiva, possono comunque essere usate in contesti professionali, per non perdere precisione nelle operazioni di editing ripetuto. Al contrario, profondità inferiori sono comunemente usate per risparmiare memoria, come nel caso di 15 bpp, che usa 5 bit per componente, o 16 bpp, che usa 6 bit per il verde, offrendo 65.536 colori diversi.
Nel caso si decida di adottare profondità molto ridotte, come 8 bpp, si preferisce ricorrere ad una modalità detta a
colore indicizzato: l’insieme dei colori
presenti nell’immagine viene
quantizzato in un insieme ridotto, i cui valori a 24 bpp sono memorizzati in una tavolozza (la
palette detta anche
colour look-up table o
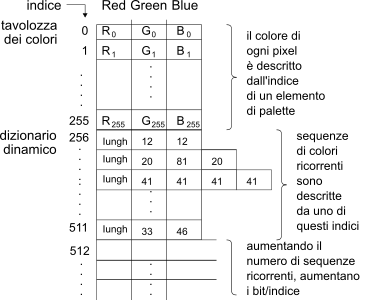
clut), che viene quindi utilizzata come un dizionario. La figura a lato mostra una immagine di esempio, assieme alla palette dei colori che usa. In questo modo, per ogni pixel dell’immagine è ora sufficiente specificare l’indice della palette dove è memorizzata la rappresentazione a 24 bpp del colore più prossimo.
Esempio Consideriamo una immagine in formato vga rappresentata mediante una palette di 256 elementi da 24 bit: ognuno dei 640x480 = 307.200 pixel può quindi assumere uno tra 256 diversi colori, scelti tra 224 = 16 milioni. La dimensione di memoria occupata si ottiene considerando che per ogni pixel occorrono 8 bit per l’indice nella palette, e che la palette stessa ha dimensioni 256x24 = 6144 bit = 768 byte, e quindi in totale 307.968 byte.
Sottocampionamento del colore
Nella tabella riportata a pag.
1 è presente la colonna
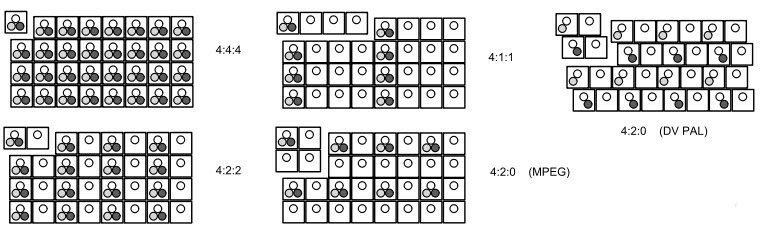
colore, che mostra come la dimensione riservata alle matrici di pixel che codificano le informazioni di crominanza sia ridotta di metà rispetto a quella della luminanza. Questo fatto trae origine da due buoni motivi: il primo è che l’acutezza visiva dell’occhio umano per ciò che riguarda le variazioni cromatiche è ridotta rispetto a quella relativa alle variazioni di luminosità; il secondo è che il segnale di crominanza presente nel segnale video composito occupa una banda circa metà di quella del segnale di luminanza. Pertanto, le componenti di luminanza sono generalmente campionate con una risoluzione spaziale inferiore a quella del segnale di luminanza. Il tipo di sotto-campionamento spaziale adottato per le componenti di crominanza è generalmente caratterizzato da quattro numeri, in accordo allo schema di fig.
10.29:
- 4:4:4 - Non si effettua sottocampionamento, e le tre componenti hanno lo stesso numero di campioni. Applicato principalmente a segnali rgb trattati in studio di produzione.
- 4:2.2 - Questo schema si applica tipicamente alle rappresentazioni ycbcr, memorizzando per ogni 4 campioni di luminanza, 2 campioni della componente cb e 2 della componente cr, ed è utilizzato in ambito professionale e broadcast.
- 4:1:1 - In questo caso ogni quattro campioni di luminanza su una riga, ne viene preso uno per cb ed uno per cr. E’ lo schema usato nello standard dv ntsc.
- 4:2:0 - Ogni 4 campioni di luminanza, ne vengono salvati uno per cb ed uno per cr come per il caso 4:1:1, ma ora la crominanza è campionata su righe alterne. In particolare, la versione utilizzata per l’mpeg-1 campiona assieme entrambi i segnali di crominanza, una riga si ed una no, mentre quella usata con il dv pal li campiona a righe alternate, e prevede una riproduzione in modalità interallacciata.
Il
Graphics Interchange Format è un formato ad 8 bpp definito da
CompuServe nel 1987 e da allora ha continuato ad essere molto popolare. Usa una
palette con cui rappresentare 256 colori scelti tra 16 milioni, e quindi comprime l’immagine mediante l’algoritmo
lzw (§
9.2.3.1), individuando sequenze ricorrenti dei valori di colore. Un singolo file può contenere più immagini (ognuna con la sua palette) in modo da realizzare brevi animazioni. Il numero ridotto di colori rende il formato poco idoneo alla riproduzione di fotografie, ma più che adatto ad immagini più semplici, come ad es. un logo di pagina web. Per rappresentare i colori assenti dalla palette, il codificatore può ricorrere ad una operazione di
dithering, alternando colori che, osservati da lontano, ricreano l’effetto della tonalità mancante.
Il metodo di compressione è illustrato con l’ausilio della figura che segue,
e adotta come anticipato l’algoritmo
lzw, il cui dizionario è inizialmente composto dalla palette, o meglio dai 256 valori ad 8 bit che indicizzano la terna
rgb a 24 bit nella palette. Quando si incontra una sequenza di codici di colore già osservata, viene aggiunta una riga al dizionario, ed il valore dell’indice corrispondente viene usato per rappresentare tutta la sotto-sequenza; eventualmente, il numero di bit usati per indicare le righe del dizionario viene aumentato di uno. Per disegnare le sequenze di pixel rappresentate da indici inclusi nella sezione dinamica della tabella, occorre dunque individuare prima le rispettive terne
rgb nella tavolozza.
Dato che la compressione lzw era stata brevettata, venne sviluppata una codifica alternativa, denominata Portable Network Graphics. Al giorno d’oggi i brevetti relativi al formato gif sono tutti scaduti, ed il formato png è stato standardizzato nella rfc 2083. Come per gif, anche png è di tipo lossless (senza perdite), ossia individua una compressione invertibile, capace di replicare in modo identico l’immagine di partenza, ovviamente senza considerare il processo di quantizzazione che porta alla generazione della palette. Oltre alla modalità di colore indicizzato, png offre anche una modalità truecolor a 24 o 32 bpp, e per questo può correttamente rappresentare anche materiale fotografico, al punto da consigliare l’uso di png (anziché jpeg) nel caso si prevedano successive operazioni di editing dell’immagine.
Per quanto riguarda la compressione, png fa uso dell’algoritmo deflate, preceduto da un passaggio di compressione differenziale, in cui al valore che rappresenta il colore di un pixel viene sottratto il valore predetto a partire dai pixel adiacenti: in tal modo l’algoritmo deflate riesce a conseguire rapporti di compressione più elevati, riuscendo quasi sempre a battere le prestazioni di gif.
10.2.4 Codifica JPEG
Il
Joint Photographic Experts Group è un comitato congiunto
iso/itu che ha definito lo standard internazionale per la compressione di immagini ISO 10918-1, particolarmente adatto alla codifica di immagini fotografiche. Descriviamo di seguito il funzionamento della modalità operativa detta
baseline, o
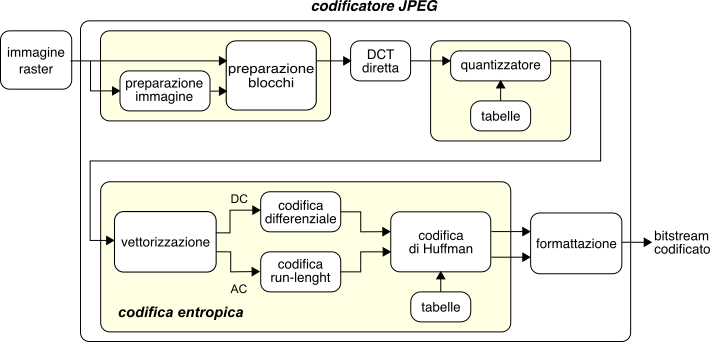
lossy sequential mode, che è quella che offre il migliore grado di compressione, e che prevede cinque stadi di elaborazione, mostrati alla fig.
10.31: preparazione dei blocchi, Discrete Cosine Transform (
dct), quantizzazione, codifica entropica, e formattazione.
Preparazione dell’immagine e dei blocchi
L’immagine raster di partenza è formata da una o più matrici bidimensionali di valori (scala di grigi, oppure a colori indicizzati, o rgb, ycrcb, yuv, ...), eventualmente di dimensioni differenti (come nel caso ycrcb). Sebbene sia possibile elaborare direttamente una rappresentazione rgb, le migliori prestazioni si ottengono nello spazio ycrcb con sotto-campionamento spaziale 4:2:2 o (meglio) 4:2:0, e dunque il primo passo è quello di convertire l’immagine in questa modalità di rappresentazione.
Ogni matrice viene quindi suddivisa in blocchi della dimensione di 8x8 pixel, ognuno dei quali è elaborato in sequenza in modo indipendente dagli altri.
Prima di procedere, la matrice Y (oppure le tre matrici
r,
g e
b) che contiene valori ad 8 bit tutti positivi, viene normalizzata sottraendo ad ogni pixel il valore 128, in modo da ottenere valori tra -128 e 127. Quindi, per ogni blocco di 8x8 pixel, i cui valori indichiamo con
p(x, y), viene calcolata una nuova matrice di 8x8 valori
D(i, j) ottenuti come coefficienti di una
trasformata coseno discreta (
dct) bidimensionale (vedi §
4.5.3):
D(i, j) = 1 4 ci cj ⎲⎳7x = 07⎲⎳y = 0p(x, y) cos(2x + 1)iπ16cos(2y + 1)jπ16
in cui
ci e
cj sono ognuno pari a
1⁄√2 con indice
i o
j pari a zero, oppure
ci = cj = 1 negli altri casi, mentre gli indici
i e
j variano tra zero e sette. Tralasciando di approfondire le relazioni esistenti tra
dct e
dft, consideriamo invece come i coefficienti
D(i, j) così ottenuti permettano la ricostruzione della matrice originaria nei termini di una somma pesata delle superfici rappresentate (per mezzo di una scala di grigi) nel diagramma riportato alla figura
10.32, mediante l’applicazione della
dct inversa
p(x, y) = 1 4 ⎲⎳7i = 07⎲⎳j = 0 ci cj D(i, j) cos(2x + 1)iπ16cos(2y + 1)jπ16
Ma se fosse tutto qui, non avremmo realizzato la funzione di compressione! Questa è infatti realizzata dalle elaborazioni successive, a partire dalla rappresentazione in termini di blocchi
dct, di cui ora approfondiamo il significato. Osserviamo quindi che ognuna delle superfici elementari rappresentate in fig.
10.32 è legata ad una coppia
i, j associata ad un coefficiente
D(i, j) della
dct calcolata, in modo che tale coefficiente esprime il contenuto di frequenze
spaziali descritto da quella particolare funzione della base. Per questo l’elemento
(i, j) = (0, 0) in alto a sinistra, ad andamento costante, è indicato come
coefficiente dc, o componente continua, dato che essendo calcolato come somma di tutti i pixel, riflette un valore che è legato alla intensità media dell’intero blocco. I coefficienti legati alle funzioni della prima riga rappresentano contenuti di frequenza spaziale orizzontale, con un periodo via via minore spostandosi verso il margine destro, mentre quelli della prima colonna, frequenze verticali. I coefficienti localizzati all’interno della matrice esprimono contenuti di frequenze spaziali in entrambe le direzioni, con valori di frequenza tanto più elevati, quanto più ci si sposta verso l’angolo in basso a destra. Pertanto, i coefficienti descritti da indici diversi da
(0, 0) sono indicati come
coefficienti ac.
L’esperienza pratica mostra come quasi sempre i coefficienti D(i, j) presentino nella regione in alto a sinistra valori ben più elevati di quelli riscontrabili in basso a destra, come conseguenza della predominanza dei blocchi posti in corrispondenza ad aree dell’immagine quasi costanti, rispetto a quelli associati alla presenza di contorni netti e particolari dettagliati.
Questo passo della elaborazione
jpeg mira a sfruttare il fenomeno percettivo della ridotta sensibilità dell’occhio umano alle frequenze spaziali più elevate, ovvero la capacità di
filtrare percettivamente le componenti di errore corrispondenti ai dettagli più minuti. Per questo, il processo di quantizzazione è orientato a ridurre, ed eventualmente sopprimere, le componenti di immagine legate alle frequenze spaziali più elevate, introducendo di fatto
una soglia sotto la quale si stabilisce di non trasmettere quelle informazioni che tanto non sarebbero percepibili. A questo scopo, ogni coefficiente
D(i, j) viene diviso per un coefficiente
Q(i, j) dipendente da
(i, j), ed il risultato viene arrotondato:
B(i, j) = round⎛⎝D(i, j)Q(i, j)⎞⎠
Il risultato corrisponde ad un processo di quantizzazione, perché quando in ricezione il processo viene invertito (ri-moltiplicando il coefficiente per la stessa quantità), viene persa la precisione legata all’arrotondamento, e pari alla metà del coefficiente di divisione. La scelta dei
Q(i, j) è fatta in modo tale da utilizzare valori più elevati per gli indici
(i, j) più elevati, in modo da ottenere due risultati: ridurre le componenti ad alta variabilità
spaziale dell’immagine, e poter usare meno bit per codificare questi valori (più piccoli). Inoltre, molti dei coefficienti con
(i, j) elevato, già piccoli di per se, quando divisi per un coefficiente di quantizzazione più elevato, non
sopravvivono all’operazione di arrotondamento, in modo che tipicamente la parte in basso a destra della matrice
B(i, j) sarà tutta pari a zero, facilitando il compito della codifica run-length dello stadio successivo.
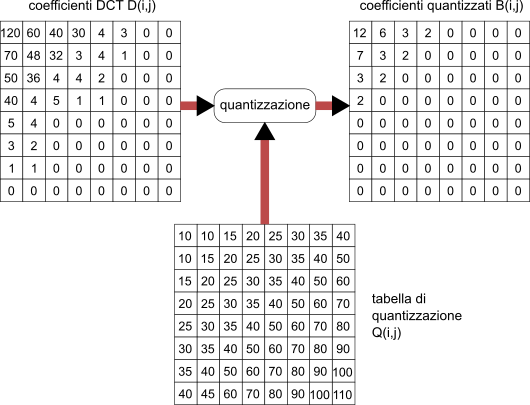
Esempio La figura
10.33 mostra un esempio di matrice di coefficienti DCT, assieme alla tabella di quantizzazione, ed al risultato dell’operazione. Notiamo come il valore dei coefficienti di quantizzazione aumenti allontanandosi dal coefficiente
dc, e come nella matrice dei coefficienti quantizzati siano
sopravvissuti solo i coefficienti relativi alle frequenze spaziali più basse.
Sebbene esistano delle tabelle di quantizzazione predefinite, i valori effettivi possono essere variati in base ad un compromesso tra qualità che si intende conseguire e fattore di compressione; tali valori vengono poi acclusi assieme al bitstream codificato durante la fase di formattazione, in modo che il processo di quantizzazione possa essere invertito nella fase di riproduzione dell’immagine.
Questo passo è un processo senza perdita, nel senso che non aggiunge altre distorsioni oltre a quelle introdotte dal passo di quantizzazione, ma è essenziale ai fini della compressione, e sfrutta le caratteristiche statistiche del risultato delle elaborazioni precedenti. Come posto in evidenza nello schema di fig.
10.31, la codifica entropica adotta due diverse procedure per i coefficienti
dc e
ac, che in entrambi i casi culminano con uno stadio di codifica a lunghezza variabile mediante codici di Huffman.
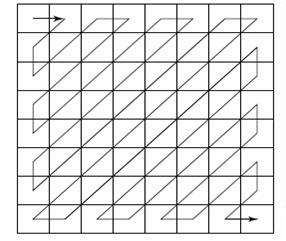
Le matrici 8x8 relative ai blocchi di elaborazione visti fin qui vengono ora trasformate in sequenze
ad una dimensione mediante un processo di scansione a
zig zag dei blocchi, il cui percorso è illustrato alla figura a lato.
La sequenza così ottenuta presenta il coefficiente
dc in testa, a cui fanno seguito i rimanenti 63 coefficienti
ac, ordinati in base al massimo valore di frequenza spaziale che rappresentano. Se applichiamo la scansione zig-zag ai valori riportati nell’esempio di fig.
10.33 otteniamo come risultato la sequenza
12 6 7 3 3 3 2 2 2 2 0 0 0 ……… 0 0
Blocchi adiacenti generalmente possiedono coefficienti dc molto simili tra loro, in virtù dell’omogeneità di ampie zone dell’immagine (pensiamo ad un porzione di cielo). Per questo motivo, anziché codificarli in modo indipendente, i singoli coefficienti dc di blocchi consecutivi vengono sottratti l’uno all’altro, e viene codificata solo la loro differenza. Ad esempio, se una sequenza di coefficienti dc risultasse pari a 12 13 11 11 10 …, il risultato di questo processo di codifica differenziale darebbe luogo alla sequenza 12 1 − 2 0 − 1 … (di fatto, il valore precedente al primo coefficiente si assume pari a zero). Dato che differenze in valore assoluto piccole sono relativamente più frequenti di differenze grandi, si è scelto di adottare per queste una codifica a lunghezza di parola variabile, realizzata
- descrivendo innanzitutto ogni valore di differenza mediante una coppia (sss, valore), in cui sss rappresenta il numero di bit necessario per rappresentare il valore, e quindi
- per ogni coppia (sss, valore) il termine sss è rappresentato mediante una codeword di Huffman, ed il valore con numero variabile di bit.
Per chiarire le idee, mostriamo le corrispondenze citate mediante due tabelle, che poi applichiamo al caso dell’esempio precedente.
| differenza |
N. di bit sss |
valore codificato |
| 0 |
0 |
|
|
| -1, 1 |
1 |
1=1 |
-1=0 |
| -3, -2, 2, 3 |
2 |
2=10 |
-2=01 |
|
|
3=11 |
-3=00 |
| -7…-4, 4…7 |
3 |
4=100 |
-4=011 |
|
|
5=101 |
-5=010 |
|
|
6=110 |
-6=001 |
|
|
7=111 |
-7=000 |
| -15…-8, 8…15 |
4 |
8=1000, |
-8=0111 |
| ⋮ |
|
⋮ |
|
|
| sss |
codeword di Huffman |
| 0 |
010 |
| 1 |
011 |
| 2 |
100 |
| 3 |
00 |
| 4 |
101 |
| 5 |
110 |
| 6 |
1110 |
| 7 |
11110 |
| ⋮ |
⋮ |
| 11 |
111111110 |
|
Tornando dunque al nostro esempio della sequenza differenziale 12 1 − 2 0 − 1 …, in termini di coppie (sss, valore) questa diviene (4, 12), (1, 1), (2, -2), (0, 0), (1, -1),... e quindi, sostituendo ad sss il relativo codice di Huffman preso dalla seconda colonna della seconda tabella, ed ai valori la loro rappresentazione indicata dalla terza colonna della prima tabella, otteniamo la sequenza di bit 101 1100, 011 1, 100 01, 010, 011 0,... in cui si sono mantenute le virgole per chiarezza. In definitiva, abbiamo usato un totale di 23 bit per rappresentare 5 differenze, che ne avrebbero richiesti 45 se codificate con 9 bit.
Viene applicata alla sequenza di coefficienti
ac che è il risultato dello
zig-zag scan. In base all’effetto congiunto delle caratteristiche dei coefficienti della
dct, e del processo di quantizzazione, la sequenza degli
ac in uscita dal vettorizzatore presenta lunghe sequenze di zeri, consentendo di conseguire buoni rapporti di compressione mediante l’uso di una codifica
run-length, realizzata scrivendo gli
ac come una sequenza di coppie
(skip, acn), in cui skip rappresenta il numero di zeri nel run, e acn è il coefficiente ac non nullo che viene dopo la sequenza di zeri. Quindi, il campo acn viene espresso a sua volta nella forma sss, valore, come indicato dalla prima tabella riportata nell’ultimo esempio. Infine, la coppia skip, sss viene rappresentata con una codeword di Huffman individuata in un nuovo codebook appositamente definito.
Esempio Applicando la codifica run-length alla sequenza dei coefficienti
ac individuati nell’esempio di vettorizzazione, ossia alla sequenza
6 7 3 3 3 2 2 2 2 0 0 0 … 0 0, si ottiene una sequenza di coppie
(skip, acn), pari a
(0,6), (0,7), (0,3), (0,3), (0,3), (0,2), (0,2), (0,2), (0,2) (0,0) in cui l’ultima coppia
(0,0) indica la fine del blocco, che in fase di decodifica viene quindi ricostruito riempiendolo di zeri. Anziché usare questa, proseguiamo adottando una diversa sequenza di coppie
(skip, acn), pari a
(0,6), (0,7), (3,3), (0,-1), (0,0): sostituendo ai termini
acn di questa, la coppia
sss, valore, e codificando quindi il termine
valore come indicato nella prima tabella dell’esempio precedente, si ottiene
(0, 3, 110), (0, 3, 111), (3, 2, 11), (0, 1, 0), (0,0). Il
bitstream finale viene quindi realizzato sostituendo alle attuali coppie
skip, sss, le rispettive codeword individuate alla colonna
Run/Size della tabella a pagina 150 e segg. delle specifiche ITU-T T.81
http://www.digicamsoft.com/itu/itu-t81-154.html, ottenendo
(100, 110), (100, 111), (111110111, 11), (00, 0), (1010), e producendo così un totale di 30 bit per rappresentare i 63 coefficienti
ac.
Lo standard
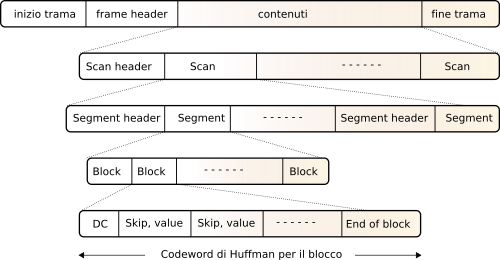
jpeg definisce, oltre alla sequenza di operazioni indicata, anche il formato di trama con il quale deve essere memorizzato il bitstream finale. La struttura risultante è gerarchica, e mostrata alla figura
10.35.
Al livello superiore troviamo un
frame header che contiene le dimensioni complessive dell’immagine, il numero ed il tipo di componenti usate (
clut,
rgb,
ycbcr, etc), ed il formato di campionamento (4:2:2, 4:2:0, etc.). Al secondo livello, troviamo uno o più
Scan, ognuno preceduto da una intestazione in cui viene riportata l’identità del componente (
r,
g,
b, o
y,
cb, cr), il numero di bit usato per rappresentare ogni coefficiente di
dct, e la tabella di quantizzazione usata per quella componente. Ogni Scan è composto da uno o più
segmenti, preceduti da un’ulteriore intestazione, che contiene il codebook di Huffman
usato per rappresentare i valori dei blocchi del segmento, nel caso non siano stati usati quelli standard. Infine, nel segmento trovano posto le sequenze di blocchi dell’immagine, così come risultano dopo lo stadio di codifica entropica.