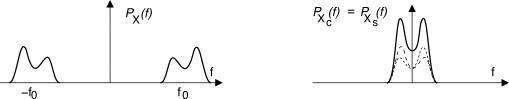Trasformata di Hilbert di un segnale modulato, spettro di processi passa banda

Prev Sezione 11.3: Densità spettrale delle c. analogiche di processi Su Capitolo 11: Segnali modulati Capitolo 12: Modulazione (e ritorno) di segnali analogici Next

11.4 Appendici

11.4.1 Filtro di Hilbert

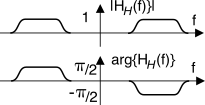
Il filtro di Hilbert è caratterizzato da una risposta in frequenza descritta analiticamente come

(14.25) H_H (f) = − j ⋅ sgn(f)

ed il cui andamento di modulo e fase può essere rappresentato come nella figura a

Filtro di Hilbert

a lato. Ricordando infatti che ± j = e^{± j π 2} e che sgn(f) = ⎧⎨⎩ 1 f > 0 −1 f < 0 , otteniamo un andamento costante del modulo |H_H(f)| = 1, ed un gradino discendente per la fase, ossia

∠H_H(f) = ⎧⎪⎨⎪⎩ − π2 f > 0 π 2 f < 0

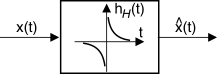
Il passaggio di un segnale x(t) attraverso il filtro di Hilbert produce un secondo segnale ^x(t) detto trasformata di Hilbert del primo, indicata come ^x(t) = H{x(t)}, ed il cui andamento in frequenza ha espressione

^X(f) = F {^x(t)} = H_H(f) X(f) = − j ⋅ sgn(f) ⋅ X(f)

ossia differisce da X(f) per uno sfasamento di ∓ π 2 per frequenze rispettivamente positive o negative. Per la trasformata di Hilbert sussistono le proprietà riportate in nota [597] [597] Per un approfondimento, vedi ad es. https://en.wikipedia.org/wiki/Hilbert_transform, di cui accenniamo brevemente solamente alcuni risultati::

H{x(t) = x₀} = 0: una costante ha trasformata di Hilbert nulla, e la trasformata di Hilbert è definita a meno di una costante. Il valore medio di x(t) non si ripercuote su ^x(t);
H{H{x(t)}} = ^^x(t) = − x(t): infatti una rotazione di fase pari a π radianti per tutte le frequenze è equivalente ad una inversione di segno;
∫^∞_−∞x(t)^x(t)dt = 0: ortogonalità tra un segnale e la sua trasformata di Hilbert;
H{x(t) * h(t)} = ^x(t) * h(t) = x(t) * ^h(t): la trasformata di Hilbert di una convoluzione (cioè dell’uscita di un filtro) è la convoluzione tra un operando trasformato e l’altro no.

Realizzazione del filtro di Hilbert

Sintetizzare un filtro che consegua esattamente la risposta in frequenza descritta dalla (14.25) è un compito pressoché impossibile, a causa della brusca transizione della fase in corrispondenza di f = 0.

In realtà, il filtro di Hilbert si usa principalmente per segnali modulati, che non presentano componenti spettrali a frequenze prossime allo zero. Pertanto, lo stesso scopo può essere svolto da un diverso filtro H_H(f), con andamento più dolce della fase, e che presenti gli stessi valori nominali del filtro di Hilbert solamente per le frequenze comprese nella banda di segnale.

Risposta impulsiva del filtro di Hilbert

Vogliamo dimostrare ora che l’antitrasformata della (14.25) risulta pari a

(14.26) h_H(t) = F ⁻¹{H_H(f)} = 1 πt

in modo da poter esprimere la trasformata di Hilbert nella forma di un integrale di convoluzione

^x(t) = H{x(t)} = 1 π ∫^∞_−∞ x(τ)t − τ dτ = x(t) * 1πt

Riutilizzando infatti un risultato trovato al § 3.8.6 siamo già arrivati a mostrare che

(14.27) F^− 1⎧⎩− j 2πf⎫⎭ = 12 sgn(t)

e dato che H_H(f) = − j ⋅ sgn(f), sembra che ci dovrebbe essere un modo semplice di arrivare a sistemare le cose. La (14.27), una volta eliminato il termine ¹⁄₂, permette di scrivere F {sgn(t)} = − j πf e dunque

(14.28) F { − j ⋅ sgn(t)} = − 1πf

Applicando ora alla (14.28) la proprietà di dualità (vedi pag. 1, dove si asserisce che se G(f) = F {g(t)}, allora F {G(t)} = g(−f)) otteniamo F ⎧⎩− 1πt⎫⎭ = − j ⋅ sgn(−f) = j ⋅ sgn(f), e dunque arriviamo al risultato anticipato

F ⁻¹{H_H(f)} = F ⁻¹{ − j ⋅ sgn(f)} = 1πt

11.4.2 Trasformata di Hilbert di un segnale modulato

Si intende dimostrare che se x_c(t) ed x_s(t) sono limitate in banda ± W con W < f₀, allora risulta

(14.29)
⎧⎨⎩ H{x_c(t)cosω₀t} = x_c(t)sinω₀t H{x_s(t)sinω₀t} = − x_s(t)cosω₀t

e dunque dalla (14.1) si ottiene

x̂(t) = H{x_c(t)cos2πf₀t − x_s(t)sin2πf₀t} = x_c(t)sinω₀t + x_s(t)cosω₀t

e quindi x̂(t) = ℑ{x(t)e^jω₀t} come espresso dall’eq. (14.10). Limitiamoci a dimostrare la prima delle (14.29), ovvero che

(14.30)
H {x_c(t)cos2πf₀t} = x_c(t)sin2πf₀t

Iniziamo con il considerare che F -trasformando l’argomento di (14.30) possiamo evidenziarne le componenti a frequenza positiva e negativa X_c(f − f₀) e X_c(f + f₀)

(14.31)
x_c(t)cos2πf₀t = x_c(t) 2(e^j2πf₀t + e^−j2πf₀t) F ⇒ 12 [X_c(f − f₀) + X_c(f + f₀)]

che, se x_c(t) ha una banda minore di f₀, possono essere facilmente H-trasformate semplicemente aggiungendo lo sfasamento introdotto a frequenze positive e negative dal filtro di Hilbert

1 2 [X_c(f − f₀) + X_c(f + f₀)] H ⇒ 12 [X_c(f − f₀)e^−jπ2 + X_c(f + f₀)e^jπ2]

e quindi F -antitrasformando questa espressione si ottiene la H-trasformata del segnale (14.30)

1 2 [X_c(f − f₀)e^−jπ2 + X_c(f + f₀)e^jπ2] F^− 1 ⇒ x_c(t) 2(e^j2πf₀te^{−jπ 2} + e^−j2πf₀te^{jπ 2})

risultato che, anche se non ancora nella forma anticipata, poteva comunque essere ottenuto anche direttamente a partire dal secondo membro di (14.31), invocando subito la limitazione ad una semibanda di x_c(t)e^±j2πf₀t. Per ottenere la (14.30) è ora sufficiente moltiplicare e dividere per j = e^jπ2, ossia

x_c(t)2(e^j2πf₀te^{−jπ 2} + e^−j2πf₀te^{jπ 2}) ⋅ e^{jπ 2} e^{jπ 2} = x_c(t) 2j(e^j2πf₀t + e^−j2πf₀te^jπ) = = x_c(t)2j(e^j2πf₀t − e^−j2πf₀t) = x_c(t)sin2πf₀t

in quanto e^jπ2 = j, e e^jπ = − 1.

11.4.3 Trasmissione a banda laterale unica

Con riferimento alla figura che segue, consideriamo un segnale a(t) reale e limitato in banda, con A(f) = A^*(−f) (grafico [a]). In virtù delle proprietà di simmetria coniugata per segnali reali la conoscenza del solo contenuto a frequenze positive

f > 0, ovvero di A⁺(f) = A(f) rect_W⎛⎝f − W 2⎞⎠, è sufficiente a definire a(t) in modo completo. Se consideriamo ora il segnale modulato x(t) = a(t)cosω₀t, anch’esso reale, otteniamo che X(f) [b], oltre ad essere a simmetria coniugata rispetto all’origine, ha simmetria coniugata anche rispetto ad f₀: X⁺(f₀ + α) = {X⁺(f₀ − α)}^*.

Questo risultato mostra come sia teoricamente possibile (con una fotocopiatrice ed un paio di forbici!) produrre un segnale Y(f) eliminando da X(f) tutta la banda |f| < f₀ [d], e quindi da quel che resta, ri-ottenere il segnale X(f) a partire da un Y(f). La ricostruzione di X(f) avviene infatti (frecce tratteggiate) spostando le copie duplicate di Y⁺(f) e Y⁻(f) come indicato dalle frecce.

Una volta verificata la correttezza ipotetica di questo procedimento che ci consente di ricevere per intero X(f) trasmettendone solo metà (cioè Y(f)), osserviamo che anche Y(f) è a simmetria coniugata rispetto a zero (ossia Y(f) = Y^*(−f)), e quindi la sua antitrasformata y(t) è reale, e dunque può essere realmente trasmesso.

A parte il “dettaglio” di come ricostruire “veramente” X(f) a partire da Y(f), ci chiediamo: esiste una formula per ottenere y(t) in modo diretto a partire da a(t)? La risposta è positiva, e si trova al § 12.1.2.

11.4.4 Processo passa banda

Svolgiamo ora l’approfondimento dei passaggi che portano ai risultati discussi al § 11.3, ovvero l’espressione della densità di potenza P_{x_c}(f) e P_{x_s}(f) in funzione di P_x(f) eq. (14.24), svolgendo i calcoli in modo da tenere in conto anche il caso dei processi aleatori: pertanto, occorrerà prima ottenere un risultato relativo alle rispettive funzioni di autocorrelazione R_{x_c}(τ) e R_{x_s}(τ), e quindi effettuare la trasformata di Fourier come prescritto dal teorema di Wiener.

Osserviamo innanzitutto che quando un processo aleatorio presenta una P_x(f) limitata in banda attorno ad f₀, la relativa funzione di autocorrelazione R_x(τ) = F ⁻¹{ P_x(f)} può essere espressa nei termini delle componenti analogiche di bassa frequenza della funzione di autocorrelazione stessa:

R_x(τ) = R_c(τ) cosω₀τ − R_s(τ) sinω₀τ

D’altra parte, una qualunque realizzazione di un processo x(t) limitato in banda attorno ad f₀ ammette la rappresentazione x(t) = x_c(t)cosω₀t − x_s(t)sinω₀t, ma data la natura aleatoria di x(t), gli stessi x_c(t) ed x_s(t) sono realizzazioni di processi, in generale statisticamente dipendenti, in quanto la loro combinazione deve produrre un x(t) che appartiene al processo originario. Si pensi ad esempio al segnale x(t) = x_c(t)cosω₀t, in cui x_c(t) è un processo stazionario ed ergodico: come già osservato al § 7.5.3, x(t) è solamente ciclostazionario [598] [598] Come illustrato al § 6.3.7, il processo risultante diviene ergodico qualora al coseno sia aggiunta una fase aleatoria uniformemente distribuita..

Come prima cosa, proviamo a calcolare la funzione di autocorrelazione dell’inviluppo complesso di una generica realizzazione, che per l’ergodicità corrisponde al relativo momento misto:

(14.32) R_x(τ) = E{x^*(τ)x(t + τ)} = = E{[x_c(τ) − jx_s(τ)][x_c(t + τ) + jx_s(t + τ)]} = = E{x_c(τ)x_c(t + τ) + x_s(τ)x_s(t + τ) + + j[x_c(τ)x_s(t + τ) − x_s(τ)x_c(t + τ)]} = = R_{x_c}(τ) + R_{x_s}(τ) + j[R_{x_cx_s}(τ) − R_{x_sx_c}(τ)]

Queste quattro quantità sono calcolate al § 11.4.5, e nel caso in cui x_c(t) e x_s(t) siano stazionari ed ergodici, il risultato finale fornisce le espressioni

(14.33)
⎧⎨⎩ R_{x_c}(τ) = R_{x_s}(τ) = R_x(τ)cosω₀τ + ^R_x(τ)sinω₀τ R_{x_cx_s}(τ) = − R_{x_sx_c}(τ) = ^R_x(τ)cosω₀τ − R_x(τ)sinω₀τ

in cui ^R_x(τ) = H{R_x(τ)} è la trasformata di Hilbert di R_x(τ). Osserviamo quindi come, sostituendo (14.33) in (14.32), risulti

(14.34) R_x(τ) = 2[R_{x_c}(τ) + jR_{x_cx_s}(τ)]

e pertanto otteniamo

(14.35)
P_x(f) = F {R_x(τ)} = 2 [P_{x_c}(f) + jP_{x_cx_s}(f)]

in cui P_{x_c}(f) = P_{x_s}(f) sono reali pari in quanto x_c(t) ed x_s(t) sono reali. Prima di giungere alle conclusioni espresse al § 11.4.4.1 ed anticipate al § 11.3, prendiamoci il lusso di sviluppare una serie di considerazioni basate sui risultati fin qui ottenuti:

la (14.35) sembra indicare che P_x(f) possa assumere valori complessi, perdendo il senso fisico di potenza, ma non è così. Osserviamo infatti che R_{x_cx_s}(τ) è un segnale reale dispari [599] [599] Infatti (eq. (14.33)) R_{x_cx_s}(τ) = ^R_x(τ)cosω₀τ − R_x(τ)sinω₀τ, in cui R_x(τ) = F ⁻¹{ P_x(f)} è pari e sinω₀t è dispari, mentre ^R_x(τ) è dispari (non è stato dimostrato, ma vale per le trasformate di Hilbert di segnali pari) e cosω₀τ è pari. Inoltre, essendo x_c(t) ed x_s(t) reali, R_{x_cx_s}(τ) è reale.: pertanto P_{x_cx_s}(f) = F {R_{x_cx_s}(τ)} è completamente immaginario, e dunque P_x(f) è reale;
se risulta R_{x_cx_s}(τ) = 0 per ogni τ, allora la potenza mutua P_{x_cx_s}(f) si annulla, e la (14.35) fornisce P_x(f) = 2 P_{x_c}(f) reale pari; la presenza di P_{x_cx_s}(f) ≠ 0 può invece rendere P_x(f) asimmetrico, permettendo di ottenere ancora P_x(f) = 4 P⁺_x(f + f₀) come espresso dalla (14.22);
invertendo i due punti precedenti osserviamo che, se P_x(f) ha simmetria pari rispetto ad f₀, allora P_x(f) è pari, e quindi deve risultare R_{x_cx_s}(τ) = 0, ovvero le c.a. di b.f. x_c(t) ed x_s(t) risultano mutuamente incorrelate; se inoltre queste sono congiuntamente gaussiane, allora risultano anche statisticamente indipendenti;
se x_c(t) e x_s(t) sono a media nulla, la potenza P_{x_c} (uguale a P_{x_s} in virtù della prima delle (14.33)) si calcola come R_{x_c}(0) = R_{x_s}(0). Dato che R_{x_cx_s}(τ) = − R_{x_sx_c}(τ) è dispari (punto 1), deve risultare che R_{x_cx_s}(0) = 0; in questo caso la (14.34) fornisce R_x(0) = 2R_{x_c}(0) = 2R_{x_s}(0), e dunque si ottiene
P_x = σ²_x = R_x(0) = 2R_{x_c}(0) = 2R_{x_s}(0) = 2σ²_{x_c} = 2σ²_{x_s} = 2 P_{x_c} = 2 P_{x_s}
In definitiva, le componenti analogiche di bassa frequenza hanno entrambe potenza pari a metà di quella dell’inviluppo complesso;
l’eq. (14.22) asserisce che P_x(f) = 4 P_x⁺(f + f₀), ed in modo simile si può trovare che P_x(f) = 4 P_x⁻(f − f₀), e quindi P_x⁺ = P_x⁻ = 14 P_x. Dato poi che P_x = P_x⁺ + P_x⁻ in quanto x⁺(t) e x⁻(t) sono ortogonali perché definiti su bande disgiunte, in base al punto 4 si ottiene
P_x = P_x⁺ + P_x⁻ = 14[ P_x + P_x] = 1 2 P_x = P_{x_c} = P_{x_s}
e dunque x_c(t) e x_s(t) hanno (ciascuno) potenza pari a quella di x(t), ovvero P_{x_c} = P_{x_s} = P_x;
se consideriamo ^x(t) l’uscita del filtro di Hilbert per il quale risulta |H_H(f)|² = 1, si ottiene che P_x̂(f) = |H_H(f)|² P_x(f) = P_x(f), e dunque antitrasformando R_^x(τ) = R_x(τ);
è possibile mostrare che, esprimendo l’autocorrelazione di x(t) in termini delle sue c.a. di b.f. R_x(τ) = R_c(τ)cosω₀τ − R_s(τ)sinω₀τ, risulta
⎧⎨⎩ R_c(τ) = R_{x_c}(τ) R_s(τ) = − R_{x_cx_s}(τ)
la prima delle (14.33) ci dice che P_{x_c}(f) = P_{x_s}(f) in quanto R_{x_c}(τ) = R_{x_s}(τ), e che risulta
R_{x_c}(τ) = R_{x_s}(τ) = R_x(τ)cosω₀τ + ^R_x(τ)sinω₀τ
applicando ora la formula di Eulero per seno e coseno si ottiene
R_{x_c}(τ) = R_{x_s}(τ) = = R_x(τ) e^jω₀τ + e^−jω₀τ 2 + ^R_x(τ) e^jω₀τ − e^−jω₀τ 2j = 1 2 [R_x(τ) − j^R_x(τ)] e^jω₀τ + 1 2 [R_x(τ) + j^R_x(τ)] e^−jω₀τ = R⁻_x(τ) e^jω₀τ + R⁺_x(τ) e^−jω₀τ
infatti i termini tra parentesi quadre corrispondono alla definizione di componenti a frequenze positive e negative ottenute tramite trasformata di Hilbert, per come espressa dalla (14.17).

11.4.4.1 Conclusioni

Al punto 8) del precedente elenco abbiamo mostrato che

R_{x_c}(τ) = R_{x_s}(τ) = R⁻_x(τ) e^jω₀τ + R⁺_x(τ) e^−jω₀τ

e quindi

P_{x_c}(f) = P_{x_s}(f) = P⁻_x(f − f₀) + P⁺_x(f + f₀)

dunque lo spettro di densità di potenza delle componenti analogiche di un processo si ottiene traslando nell’origine e sovrapponendo (vedi fig. 11.31) le componenti a frequenze positive e negative dello spettro di densità di potenza P_x(f) del segnale modulato. Dunque P_{x_c}(f) e P_{x_s}(f) sono entrambe pari, come deve essere per x_c(t) ed x_s(t) reali.

Figure 11.31 Processo passa banda e densità di potenza delle c.a. di b.f.

11.4.4.2 Processo gaussiano bianco limitato in banda

Se x(t) è un processo gaussiano stazionario ergodico, bianco ed a media nulla, con densità spettrale P_x(f) = N₀ 2 limitata in banda ± W attorno ad f₀, allora (vedi fig. 11.32)

le relative c.a. di b.f. x_c(t) e x_s(t) sono processi congiuntamente gaussiani, stazionari, ergodici, statisticamente indipendenti ed a media nulla, con potenza P_{x_c} = P_{x_s} = P_x = 2N₀W, pari alle varianze σ²_x = σ²_{x_c} = σ²_{x_s}. Le rispettive densità di potenza valgono
(14.36)
P_{x_c}(f) = P_{x_s}(f) = P⁺_x(f + f₀) + P⁻_x(f − f₀) = N₀rect_2W(f)
il suo inviluppo complesso x(t) relativo ad f₀ ha potenza (e densità di potenza) doppie
(14.37)
P_x = 2 P_{x_c} = 4N₀W; P_x(f) = 2N₀rect_2W(f)

Infatti la simmetria pari di P_x(f) attorno ad f₀ rende x_c(t) e x_s(t) incorrelate, come mostrato al punto 3) di pag. 1: pertanto P_{x_cx_s}(f) = F {R_{x_cx_s}(τ)} = 0 (punto 2) e dunque la (14.35) si semplifica nella (14.37).

Figure 11.32 Densità di potenza delle c.a. di b.f. per un processo gaussiano bianco e limitato e limitato in banda

11.4.5 Autocorrelazione di processi passa-banda

Svolgiamo qui il calcolo relativo al valore di R_{x_c}(τ), R_{x_s}(τ), R_{x_cx_s}(τ) e R_{x_sx_c}(τ). Ricordando che (pag. 1) x_c(t) = x(t)cosω₀t + ^x(t)sinω₀t, iniziamo a svolgere i calcoli per R_{x_c}(τ):

R_{x_c}(τ) = E{x_c(τ)x_c(t + τ)} = = E{[x(t)cosω₀t + ^x(t)sinω₀t] ⋅ ⋅ [x(t + τ)cosω₀(t + τ) + ^x(t + τ)sinω₀(t + τ)]} = = E{x(t)x(t + τ)} ⋅ cosω₀t ⋅ cosω₀(t + τ) + + E{x(t)^x(t + τ)} ⋅ cosω₀t ⋅ sinω₀(t + τ) + + E{^x(t)x(t + τ)} ⋅ sinω₀t ⋅ cosω₀(t + τ) + + E{^x(t)^x(t + τ)} ⋅ sinω₀t ⋅ sinω₀(t + τ)

Valutiamo quindi singolarmente i quattro valori attesi, procedendo con il calcolo di medie temporali in virtù dell’ergodicità, e indicando con x(t) la media temporale di x(t), ossia x(t) = lim_{T → ∞} 1T ∫^T ⁄ 2_{− T ⁄ 2}x(t)dt:

E{x(t)x(t + τ)} = x(t)x(t + τ) = R_x(τ) E{x(t)^x(t + τ)} = x(t)^x(t + τ) = R_x^x(τ) = x(−τ) * ^x(τ) = = x(−τ) * x(τ) * 1 πτ = R_x(τ) * 1 πτ = ^R_x(τ) E{^x(t)x(t + τ)} = ^x(t)x(t + τ) = R_^xx(τ) = ^x(−τ) * x(τ) = = x(−τ) * ⎛⎝− 1 πτ⎞⎠ * x(τ) = x(−τ) * x(τ) * ⎛⎝− 1 πτ⎞⎠ = = R_x(τ) * ⎛⎝− 1 πτ⎞⎠ = − ^R_x(τ) E{^x(t)^x(t + τ)} = ^x(t)^x(t + τ) = R_^x^x(τ) = ^x(−τ) * ^x(τ) = = x(−τ) * ⎛⎝− 1 πτ⎞⎠ * x(τ) * 1 πτ = = x(−τ) * x(τ) * ⎛⎝− 1 πτ⎞⎠ * 1 πτ = − ^^R_x(τ) = R_x(τ)

Sostituendo le relazioni ora trovate nella espressione di R_{x_c}(τ), si ottiene

R_{x_c}(τ) = R_x(τ) ⋅ cosω₀t ⋅cosω₀(t + τ) + ^R_x(τ) ⋅ cosω₀t ⋅sinω₀(t + τ) + − ^R_x(τ) ⋅ sinω₀t ⋅cosω₀(t + τ) + R_x(τ) ⋅ sinω₀t ⋅sinω₀(t + τ) = = 1 2 R_x(τ)[cosω₀(−τ) + cosω₀(2t + τ)] + + 12 ^R_x(τ)[sinω₀(τ) + sinω₀(2t + τ)] + − 12 ^R_x(τ)[sinω₀(−τ) + sinω₀(2t + τ)] + + 12 R_x(τ)[cosω₀(−τ) − cosω₀(2t + τ)] = = R_x(τ) ⋅ cosω₀τ + ^R_x(τ) ⋅ sinω₀τ

che costituisce il risultato anticipato alla (14.33). Per l’espansione dei termini trigonometrici, si è fatto uso delle relazioni

cosα ⋅ cosβ = 1 2 [cos(α − β) + cos(α + β)] sinα ⋅ sinβ = 1 2 [cos(α − β) − cos(α + β)] sinα ⋅ cosβ = 1 2 [sin(α − β) + sin(α + β)]

I calcoli relativi al valore di R_{x_s}(τ) sono del tutto simili, ed il loro svolgimento porta al risultato R_{x_c}(τ) = R_{x_s}(τ).

Per quanto riguarda R_{x_cx_s}(τ) applichiamo la relazione x_s(t) = ^x(t)cosω₀t − x(t)sinω₀t per ottenere

R_{x_cx_s}(τ) = E{x_c(τ)x_s(t + τ)} = = E{[x(t)cosω₀t + ^x(t)sinω₀t] ⋅ ⋅ [^x(t + τ)cosω₀(t + τ) − x(t + τ)sinω₀(t + τ)] = = E{x(t)^x(t + τ)} ⋅ cosω₀t ⋅ cosω₀(t + τ) + − E{x(t)x(t + τ)} ⋅ cosω₀t ⋅ sinω₀(t + τ) + + E{^x(t)^x(t + τ)} ⋅ sinω₀t ⋅ cosω₀(t + τ) + − E{^x(t)x(t + τ)} ⋅ sinω₀t ⋅ sinω₀(t + τ)

I valori attesi che vediamo comparire sono già stati ricavati e quindi possiamo scrivere direttamente lo sviluppo dei calcoli, in cui si applicano nuovamente le identità trigonometriche note:

R_{x_cx_s}(τ) = ^R_x(τ) ⋅ cosω₀t ⋅ cosω₀(t + τ) − R_x(τ) ⋅ cosω₀t ⋅ sinω₀(t + τ) + + R_x(τ) ⋅ sinω₀t ⋅ cosω₀(t + τ) + ^R_x(τ) ⋅ sinω₀t ⋅ sinω₀(t + τ) = = 1 2 ^R_x(τ)[cosω₀(−τ) + cosω₀(2t + τ)] + − 12 R_x(τ)[sinω₀(τ) + sinω₀(2t + τ)] + + 12 R_x(τ)[sinω₀(−τ) + sinω₀(2t + τ)] + + 12 ^R_x(τ)[cosω₀(−τ) − cosω₀(2t + τ)] = = − R_x(τ) ⋅ sinω₀τ + ^R_x(τ) ⋅ cosω₀τ

ottenendo così il risultato preannunciato alla (14.33).

I calcoli relativi al valore di R_{x_sx_c}(τ) sono del tutto simili, ed il loro svolgimento porta al risultato R_{x_sx_c}(τ) = − R_{x_cx_s}(τ).

Prev Sezione 11.3: Densità spettrale delle c. analogiche di processi Su Capitolo 11: Segnali modulati Capitolo 12: Modulazione (e ritorno) di segnali analogici Next