Processi stazionari ed ergodici

Prev Sezione 6.2: Variabili aleatorie Su Capitolo 6: Probabilità processi e statistica Sezione 6.4: Trasformazione di v.a. e cambio di variabili Next

6.3 Processi stazionari ed ergodici

Dopo aver descritto come caratterizzare statisticamente i valori di v.a. singole o vettoriali, occupiamoci del caso in cui si voglia descrivere da un punto di vista probabilistico un intero segnale, la cui reale identità non sia nota a priori [280] [280] Chiaramente, la maggioranza dei segnali trasmessi da apparati di tlc sono di questo tipo..

Figure 6.10 Un processo non ergodico

Un segnale siffatto viene detto membro (o realizzazione) di un processo aleatorio, e può essere indicato come x(t, θ), mediante una descrizione formale che prevede una coppia di insiemi: il primo di questi è l’insieme T degli istanti temporali (tipicamente entro un intervallo) su cui sono definiti i membri del processo, mentre il secondo è relativo ad una variabile aleatoria Θ, i cui valori θ identificano ognuno una particolare realizzazione del processo. Pertanto, una specifica realizzazione θ_i della v.a. Θ indicizza il processo, i cui membri x(t, θ_i), con t ∈ T, sono noti solo dopo la conoscenza di θ_i ∈ Θ ( [281] [281] Per fissare le idee, conduciamo parallelamente al testo un esempio “reale” in cui il processo aleatorio è costituito da.... la selezione musicale svolta da un dj. L’insieme T sarà allora costituito dall’orario di apertura delle discoteche (dalle 22 all’alba ?), mentre in θ faremo ricadere tutte le caratteristiche di variabilità (umore del dj, i dischi che ha in valigia, la discoteca in cui ci troviamo, il giorno della settimana...).). Il processo aleatorio è quindi definito come l’insieme dei segnali {x(t, θ)}, con t ∈ T e θ ∈ Θ.

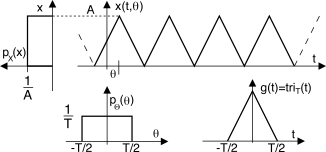
Se viceversa fissiamo un particolare istante temporale t_j, il valore x(t_j, θ) è una variabile aleatoria, la cui realizzazione dipende da quella di θ ∈ Θ; pertanto, è definita la densità p_X(x(t_j)) (indipendente da θ), che possiamo disegnare in corrispondenza dell’istante t_j in cui è prelevato il campione [282] [282] Nell’esempio, x(t₀, θ) è il valore di pressione sonora rilevabile ad un determinato istante (es. le 23.30) al variare di θ (qualunque dj, discoteca, giorno...).; a tale riguardo, si faccia riferimento alla figura 6.10, che mostra le densità di probabilità definite e riferite a membri di un processo.

6.3.1 Momento come media di insieme

Consiste nel valore atteso di una potenza n-esima dei valori del segnale, eseguito rispetto alla variabilità dovuta a Θ, ed è pertanto calcolata come

m⁽ⁿ⁾_X(t_j) = E_Θ{xⁿ(t_j, θ)} = ^∞⌠⌡_−∞xⁿ(t_j, θ)p_Θ(θ)dθ = ^∞⌠⌡_−∞xⁿp_X(x(t_j))dx

in cui l’ultima eguaglianza indica come la variabilità statistica di xⁿ sia completamente descritta dalla d.d.p. p_X(x(t_j)) di x(t_j, θ) al variare di θ ∈ Θ, mostrata in basso in fig. 6.10. Notiamo che secondo questo approccio, la media di insieme dipende dall’istante t_j in cui è prelevato un valore [283] [283] Ad esempio, se in tutte le serate il volume aumenta progressivamente nel tempo, la p_X(x(t_j)) si allargherà per t_j crescenti..

6.3.2 Media temporale

In alternativa, possiamo fissare una particolare realizzazione θ_i di Θ, e quindi concentrare l’attenzione su di un singolo membro x(t, θ_i), che è ora un segnale certo [284] [284] x(t, θ_i) rappresenta, nel nostro esempio, l’intera selezione musicale (detta serata) proposta da un ben preciso dj, in un preciso locale, un giorno ben preciso.: per esso possono quindi essere calcolate le medie temporali, indicate con una linea sopra alla quantità di cui si calcola la media (.):

xⁿ(t, θ_i) = lim_{T → ∞} 1 T ^T ⁄ 2⌠⌡_{− T ⁄ 2}xⁿ(t, θ_i)dt

In particolare, troviamo il valore medio (pag. 1)

x(t, θ_i) = lim_{T → ∞} 1 T ^T ⁄ 2⌠⌡_{− T ⁄ 2}x(t, θ_i)dt

e la potenza [285] [285] m⁽²⁾_X(θ_i) in questo caso rappresenta la potenza media con cui è suonata la musica nella particolare serata θ_i. (eq. (1.1)) (o media quadratica)

x²(t, θ_i) = lim_{T → ∞} 1 T ^T ⁄ 2⌠⌡_{− T ⁄ 2}x²(t, θ_i)dt

Notiamo che una generica media temporale:

non dipende dal tempo;
è una variabile aleatoria, in quanto dipende dalla realizzazione di Θ.

6.3.3 Media temporale calcolata come media di insieme

L’estrazione da x(t, θ_i) di un valore ad un istante casuale t ∈ T definisce una ulteriore variabile aleatoria, descritta dalla densità di probabilità (condizionata) p_X(x ⁄ θ_i), che disegniamo a fianco dei singoli membri mostrati in fig. 6.10. Qualora la p_X(x ⁄ θ_i) sia nota, le medie temporali di ordine n possono essere calcolate (per quel membro) come i rispettivi momenti:

xⁿ(t, θ_i) = lim_{T → ∞} 1 T ^T ⁄ 2⌠⌡_{− T ⁄ 2}xⁿ(t, θ_i)dt = ^∞⌠⌡_−∞xⁿp_X(x ⁄ θ_i)dx = E_{X ⁄ Θ = θ_i}{xⁿ} = m⁽ⁿ⁾_X(θ_i)

Ciò equivale infatti ad effettuare una media ponderata, in cui ogni possibile valore di x è pesato per la sua probabilità p_X(x ⁄ θ_i)dx (vedi l’esempio a pag. 1).

6.3.4 Processo stazionario

Qualora p_X(x(t_j)) non dipenda da t_j, ma risulti p_X(x(t_j)) = p^T_X(x) per qualsiasi t_j ∈ T, il processo {x(t, θ)} è detto stazionario [286] [286] La “serata in discoteca” stazionaria si verifica pertanto se non mutano nel tempo il genere di musica, il volume dell’amplificazione... o meglio se eventuali variazioni in alcune particolari discoteche-realizzazioni sono compensate da variazioni opposte in altrettanti differenti membri del processo. in senso stretto. In tal caso tutte le medie di insieme non dipendono più dal tempo, ossia m⁽ⁿ⁾_X(t) = m⁽ⁿ⁾_X per ∀t ∈ T, e le p_X(x(t_j)) in basso in fig. 6.10 sono tutte uguali.

Se invece sono solamente le prime due medie di insieme m_X(t) e m⁽²⁾_X(t) a non dipendere da t, il processo {x(t, θ)} è detto stazionario in media ed in media quadratica, od anche stazionario in senso lato [287] [287] In questo caso la p_X(x(t)) non è nota, oppure non è stazionaria, ma le maggiori applicazioni della proprietà di stazionarietà dipendono solo da m_X(t) e m⁽²⁾_X(t), che possono essere misurati (o per meglio dire stimati, vedi § 6.6.3.1), e risultare stazionari anche se p_X(x(t)) non lo è.. Nel caso di un processo gaussiano (§ 6.5.3), la stazionarietà in senso lato implica quella in senso stretto [288] [288] Infatti la d.d.p. gaussiana è completamente definita qualora siano noti i valori di media e (co)varianza, vedi §§ 6.2.4 e 6.5. .

Supponiamo ora di suddividere il membro x(t, θ_i) in più intervalli temporali, e di calcolare per ciascuno di essi le medie temporali, limitatamente al relativo intervallo. Nel caso in cui queste risultino uguali tra loro, e di conseguenza uguali alla media temporale m⁽ⁿ⁾_X(θ_i), il membro è (individualmente) stazionario [289] [289] Questo accade se la selezione musicale di una particolare serata si mantiene costante (es. solo raggamuffin) oppure variata ma in modo omogeneo (es. senza tre “lenti” di fila).. Ovviamente, se tutti i membri sono individualmente stazionari, lo è anche il processo a cui appartengono.

6.3.5 Processo stazionario ed ergodico

Questa importante sottoclasse di processi stazionari identifica la circostanza che ogni membro del processo è statisticamente rappresentativo di tutti gli altri. Ciò si verifica quando la densità di probabilità (a destra in fig. 6.10) dei valori estratti da un singolo membro p_X(x ⁄ θ_i) è sempre la stessa, indipendentemente dal particolare θ_i, ottenendo in definitiva p_X(x ⁄ θ_i) = p^Θ_X(x) indipendentemente dalla realizzazione e, per la stazionarietà, anche p_X(x ⁄ t_j) = p^T_X(x), e dunque p^Θ_X(x) = p^T_X(x) = p_X(x). In questo caso le medie temporali m⁽ⁿ⁾_X(θ_i), calcolabili come momenti sulla singola realizzazione come illustrato al § 6.3.3, sono identiche per tutti i membri [290] [290] Volendo pertanto giungere alla definizione di una serata ergodica in discoteca, dovremmo eliminare quei casi che, anche se individualmente stazionari, sono decisamente “fuori standard” (tutto metal, solo liscio...). θ_i, ed identiche anche alle medie di insieme m⁽ⁿ⁾_X(t_j) calcolate per un qualunque istante. Enunciamo pertanto la definizione:

Un processo stazionario è ergodico se la media temporale calcolata su di una qualunque realizzazione del processo, coincide con la media di insieme relativa ad una variabile aleatoria estratta ad un istante qualsiasi (per la stazionarietà) dall’insieme dei suoi membri.

Esempio: la potenza di segnale Mostriamo come il calcolo della potenza di un membro di un processo ergodico sia equivalente a quello del momento di 2^o ordine del processo:

P_X(θ) = x²(θ) = lim_{T → ∞} 1 T ^T ⁄ 2⌠⌡_{− T ⁄ 2}x²(t, θ) dt = ^∞⌠⌡_−∞x² p_X(x ⁄ θ) dx = = ^∞⌠⌡_−∞x² p_X(x) dx = m⁽²⁾_X = E{x²} = P_X

Questo risultato mostra come sia possibile calcolare la potenza di una realizzazione di un processo, senza conoscere la forma d’onda dei suoi membri.

Esempio: il valore medio A pag. 1 è stato definito come x = lim_{T → ∞} 1 T ∫^T ⁄ 2_{− T ⁄ 2}x(t)dt, ovvero come una media temporale del primo ordine. Qualora x(t) sia membro di un processo ergodico, tale valore può esser calcolato anche come valore atteso di x(t), ovvero momento di primo ordine m_x della v.a. x estratta dal processo:

x(θ) = lim_{T → ∞} 1 T ^T ⁄ 2⌠⌡_{− T ⁄ 2}x(t, θ) dt = ^∞⌠⌡_−∞x p_X(x ⁄ θ) dx = = ^∞⌠⌡_−∞x p_X(x) dx = E{x} = m_X

Potenza, varianza, media quadratica e valore efficace

In particolare osserviamo che in base alla (10.119) possiamo scrivere

(10.125) P_X = m⁽²⁾_X = σ²_x + (m_x)²

e per i segnali a media nulla (m_x = 0) si ottiene P_X = σ²_x; in tal caso il valore efficace (pag. 1) √ P_X coincide con la deviazione standard σ_x. La radice della potenza è inoltre spesso indicata come valore RMS (root mean square), definito come x_RMS = √x²(t) , ovvero la radice della media quadratica (nel tempo). Se il segnale è a media nulla, x_RMS coincide quindi con il valore efficace; se x(t) è membro di un processo ergodico a media nulla, x_RMS coincide con la deviazione standard.

6.3.6 Riassumendo

Se un processo è ergodico, è anche stazionario, ma non il viceversa. Esempio: se x(t, θ) = C_θ pari ad una costante (aleatoria), allora è senz’altro stazionario, ma p_X(x ⁄ θ) = δ(x − C_θ), e quindi non ergodico.
Se un processo è ergodico è possibile:
- calcolare le medie di insieme in forma di medie temporali a partire da una singola realizzazione oppure
- ottenere le medie temporali di una qualunque realizzazione a partire dalle medie di insieme, disponendo della statistica p_X(x), e anche
- stimare la d.d.p. a partire dall’istogramma dei valori estratti da un qualunque membro.
Se l’eguaglianza tra medie di insieme e temporali sussiste solo fino ad un determinato ordine e non oltre, il processo non è ergodico in senso stretto. Per ciò che concerne le telecomunicazioni, è spesso sufficiente la proprietà di ergodicità in senso lato, ovvero limitata al 2^o ordine, che garantisce x(t) = E{x} = m_x; x²(t) = E{x²} = m⁽²⁾_x.

6.3.7 Processo ad aleatorietà parametrica

A volte può convenire pensare un segnale certo come rappresentante di una intera classe di segnali che definiscono un processo ergodico, in modo da poter calcolare le medie temporali che lo riguardano mediante delle medie di insieme. In tal caso si rientra nella categoria di processi parametrici {x(t, θ)} in cui la v.a. θ compare in modo esplicito nella espressione analitica dei segnali membri. Ad esempio, il segnale periodico

(10.126) x(t, θ) = ^∞⎲⎳_{n = −∞}A ⋅ g_T(t − θ − nT)

rappresentato alla figura di lato, ha come parametro aleatorio un ritardo θ, che ne rende imprecisata la fase iniziale. Se θ è (come in figura) una v.a. a distribuzione uniforme tra − ^T⁄₂ e ^T⁄₂ (ovvero p_Θ(θ) = 1 T rect_T(θ)), allora il processo (10.126) risulta stazionario ed ergodico. Infatti scegliendo ad esempio una g(t) = tri_T(t) la d.d.p. per una v.a. estratta dal processo ad un istante qualunque diviene pari a [291] [291] La (10.127) non è frutto di un calcolo, bensì di un ragionamento: l’impulso g_T(t) triangolare non “passa più tempo” su di un valore o su di un altro, ma passa lo stesso tempo su un qualunque valore tra 0 ed A. Pertanto i diversi membri del processo, ognuno relativo ad un diverso θ, qualora valutati ad un medesimo istante t, assumono uno qualsiasi dei valori tra 0 ed A con d.d.p. uniforme.

(10.127) p_X(x) = 1 A rect_A (x − A 2 )

uguale cioè alla d.d.p. ottenibile estraendo una v.a. da un membro qualunque.

Esercizio Possiamo verificare la coincidenza tra medie temporali e di insieme, osservando che il valor medio m_X = E{x} di un qualunque membro di (10.126) è pari alla media temporale A2, la varianza è pari a quella della d.d.p. uniforme σ²_X = A² 12 (§ 6.2.3), e la potenza vale [292] [292] Verifichiamo per esercizio che il valore (10.128) corrisponda a quello calcolato come media temporale. Calcoliamo innanzitutto l’energia E_g di g(t) :

E_g = 2^{− ^T⁄₂}⌠⌡₀[g(t)]²dt = 2^{− ^T⁄₂}⌠⌡₀ ⎡ ⎣1 − 2tT ⎤⎦²dt = 2^{− ^T⁄₂}⌠⌡₀ ⎡ ⎣1 + 4t² T² − 4t T ⎤ ⎦²dt = = 2 ⎛ ⎝T2 + 4T² t³ 3 | |^{^T⁄₂}₀ − 4 T t² 2 | |^{^T⁄₂}₀⎞⎠ = T + 8T² T³ 3 ⋅ 8 − 8 T T² 2 ⋅ 4 = T + T3 − T = T3

da cui la potenza di x(t) si ottiene come P_X = A²^E_g⁄_T = A² 3 .

(10.128)
P_X = σ²_X + m²_X = A² 12 + A² 4 = 4A² 12 = A² 3

Se la p_Θ(θ) fosse stata diversa, il processo avrebbe perso stazionarietà e quindi ergodicità. Infatti, ponendo ad esempio p_Θ(θ) = 2 T rect_{T 2}(θ) e volendo ottenere una media di insieme considerando i possibili membri del processo nell’intervallo temporale − ^T⁄₄ < t < ^T⁄₄, tutte le realizzazioni avrebbero valori maggiori del valor medio A2.

Processo armonico

Si tratta di un processo ad aleatorietà parametrica, i cui membri

Figure 6.12 Densità di prob. per un processo armonico

hanno espressione

x(t, θ) = Acos(2πf₀t + θ)

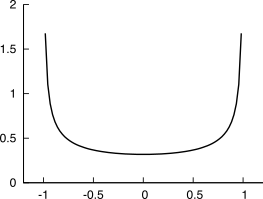
dove θ è una v.a. uniforme con d.d.p. p_Θ(θ) = 12π rect_2π(θ). In tal caso il processo è stazionario ed ergodico, ed a pag. 1 si dimostra che un valore estratto a caso da un membro qualsiasi è una v.a. con d.d.p.

(10.129) p_X(x) = 1 π√A² − x²

mostrata in figura 6.12, la cui sagoma è detta a vasca da bagno (bathtube).

Segnale dati

Anticipiamo l’espressione (21.1) a cui aggiungiamo un elemento di indeterminazione per quanto riguarda la relazione temporale tra l’origine dei tempi e gli istanti caratteristici, scrivendo

(10.130) x(t, θ) = ^∞⎲⎳_{n = −∞}a_ng(t − nT + θ)

con θ v.a. a distribuzione uniforme tra ± T2, in modo da rendere il processo ergodico [293] [293] In assenza del parametro θ, e considerando la sequenza aleatoria degli a_n stazionaria ed ergodica, x(t, θ = 0) costituisce un processo ciclostazionario in senso stretto (vedi https://en.wikipedia.org/wiki/Cyclostationary_process), ossia per il quale le medie di insieme di qualsiasi ordine sono periodiche di periodo T. La presenza della v.a. uniforme θ rende x(t, θ) un processo stazionario, ed anche ergodico.. Mentre il calcolo della sua densità di potenza sarà affrontato al § 7.2.5, qui ci limitiamo ad osservare che, considerando i valori a_n come determinazioni di v.a. indipendenti ed identicamente distribuite, la densità di probabilità di x(t) può euristicamente essere desunta dalla analisi del corrispettivo diagramma ad occhio (§ 15.1.2.3). Ad esempio, nel caso di g(t) rettangolare e a_n a due livelli equiprobabili (vedi fig. 15.7 a pag. 1) la p_X(x) sarà costituita da due impulsi di area ¹⁄₂, mentre nei casi di limitazione in banda e/o adozione di un impulso con caratteristica a coseno rialzato, la stessa assumerà un andamento continuo [294] [294] In una futura edizione, potrei calcolare le ddp corrispondenti ai diagrammi ad occhio di fig. 15.23.

Prev Sezione 6.2: Variabili aleatorie Su Capitolo 6: Probabilità processi e statistica Sezione 6.4: Trasformazione di v.a. e cambio di variabili Next