Sezione 14.1: Il rumore additivo nei segnali modulati Su Capitolo 14: Prestazioni delle trasmissioni modulate Sezione 14.3: Prestazioni della modulazione di frequenza 

14.2 Prestazioni delle trasmissioni AM

Esprimiamo innanzitutto il segnale modulato nei termini delle sue componenti analogiche
xAM(t) = xc(t) cosω0t − xs(t) sinω0t
a cui sommare il rumore filtrato ν(t) (eq. (14.90)).
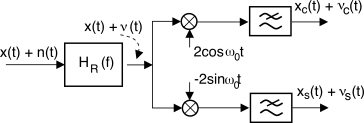
figure f95.5.png
All’uscita da un demodulatore coerente in fase e quadratura (§ 12.2.3.1) si osserva quindi un segnale d(t) espresso dalle relative c.a di b.f.
⎧⎨⎩ dc(t) = xc(t) + νc(t)   ds(t) = xs(t) + νs(t)
mentre tra la potenza del segnale ricevuto x(t) e quella delle sue c.a. di b.f. sussiste [685]   [685]  Infatti i segnali xc(t)cosω0t e xs(t)sinω0t risultano ortogonali, e le potenze si sommano. Volendo sviluppare i calcoli, possiamo valutare Px come
Px  = E{(xAM(t))2} = E{(xc(t)cosω0t − xs(t)sinω0t)2} =       = E{(xc(t)cosω0t)2} + E{(xs(t)sinω0t)2} − 2E{xc(t)xs(t)cosω0tsinω0t}
Possiamo ora aggiungere ad entrambe le portanti una fase aleatoria uniforme in modo da renderle anch’esse processi, indipendenti da xc(t) ed xs(t). Al § 7.5.3 si è mostrato che il prodotto di processi indipendenti ed a media nulla ha potenza pari al prodotto delle potenze, e dunque i primi due termini sono rispettivamente pari a 12 Pxc e 12 Pxv. Per quanto riguarda il terzo termine, esso rappresenta il valore atteso del prodotto di processi indipendenti ed a media nulla, e dunque è nullo. Infine, sviluppando i calcoli a partire dalle medie temporali anziché di insieme si perviene al medesimo risultato.
la relazione
(14.92) Px = 12 Pxc + 12 Pxs

14.2.1 Potenza di segnale e di rumore dopo demodulazione ed SNR

Nel caso di modulazione am il segnale modulante viene ricavato a partire dalla sola componente in fase dc(t) = xc(t) + νc(t), i cui termini identifichiamo come componenti di segnale e di rumore, ottenendo così l’SNR dopo demodulazione
(14.93) SNRd = PxcPνc
Il valore della (14.93) per il caso di modulazione bld-ps, blu-ps e bld-pi (cap. 12) è calcolato ai §§ seguenti a partire dall’espressione
xBLD(t) = xc(t) cosω0t = (ap + m(t)) cosω0t
a parità di SNR0, ossia considerando fissi W (di m(t)), N0 (del rumore) e la Px ricevuta, ed i risultati riportati in tab. [686]   [686] La tabella estende quella al § 12.1.4, rispetto alla quale si considera il termine ka ora inglobato in m(t). 14.1 assieme alle grandezze che concorrono al calcolo.

xc(t)
Px
Pxc
BN
Pνc
SNR
BLD-PS m(t)
12 Pm
Pm = 2 Px
2W
2WN0
PxWN0 = SNR0
BLU-PS 1√2m(t)
12 Pm
12 Pm = Px
W
WN0
SNR0
BLD-PI √η(ap + m(t))
12 Pm
ηPm = 2ηPx
2W
2WN0
η ⋅ SNR0
Table 14.1 Potenza di segnale e di rumore dopo demodulazione am
La banda di rumore (§ 14.1.2) indicata in tabella è la minima possibile, pari a quella del segnale modulato BRF, direttamente legata (nella modulazione am) a quella (± W) del segnale modulante. Pertanto i risultati che otteniamo sono i migliori possibili, dato che se BN > BRF, l’SNR risulterà peggiore.

14.2.1.1 Modulazione BLD-PS

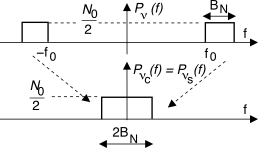
La prima riga di tab. 14.1 riassume come per xAM(t) = m(t)cosω0t si ottenga Px = 12 Pm ovvero Pm = 2 Px, e dato che Pxc = Pm, a numeratore della (14.93) possiamo scrivere Pxc = Pm = 2 Px. Per quanto riguarda il denominatore, nel caso bld la banda di x(t) è pari a 2W ovvero al doppio di quella di m(t), e quindi con una densità Pνc(f) = N0 (vedi fig. 14.4) la potenza di rumore vale Pνc = 2WN0, e dunque
SNRBLD = PxcPνc = 2 Px2WN0 =  PxWN0 = SNR0
ovvero le prestazioni dopo demodulazione sono esattamente pari all’SNR0 di riferimento definito al § 14.1.4: dunque la modulazione bld-ps non altera il rapporto SNR0 di banda base, ovvero è come se il processo di modulazione fosse trasparente.

14.2.1.2 Modulazione BLU-PS

In questo caso si ha
xAM(t) = 1√2 m(t) cosω0t − 1√2 m̂(t) sinω0t
(vedi § 12.1.4 e 12.4.5) da cui si può ottenere [687]   [687] Riprendendo l’approccio adottato alla nota 685, consideriamo le portanti in fase e quadratura come realizzazioni di un processo armonico con potenza 1⁄2, moltiplicate per un processo statisticamente indipendente m(t)⁄√2 con potenza Pm⁄2. La potenza di ciascuna c.a. di b.f. è il prodotto di queste due, e dunque partendo dalla (14.92)
Px  = 12  Pxc + 12  Pxs = 12 ⋅ 2 ⋅ Pxc = 1 ⋅ 12 ⋅  Pm = 12 ⋅  Pm
Px = 12 Pm come per il caso bld-ps, e dato che ora risulta Pxc = E{(1√2m(t))2} = 12 Pm, al numeratore di (14.93) possiamo scrivere Pxc = Px, la metà del caso precedente.
figure f95.6.png
Per quanto riguarda invece la componente di rumore, alla figura a lato si mostra come anche la densità di potenza Pν(f) del rumore che attraversa HR(f) occupa una banda a sua volta dimezzata, e quindi dopo demodulazione la densità di potenza Pνc(f) occupa una banda ± BN come nel caso am-bld, ma possiede una valore N0⁄2 uguale a quello della Pν(f) in ingresso, e non doppio come al § 14.1.3.
Pertanto la potenza Pνc del rumore demodulato sul ramo in fase (con un filtro HR(f) ideale ed a banda minima BN = W) è pari a 2W ⋅ N0⁄2 = WN0,  permettendo di scrivere
SNRBLU = PxcPνc = PxWN0 = SNR0
e cioè si ottengono prestazioni identiche a quelle del caso am-bld, ma utilizzando solo metà della banda altrimenti necessaria.

14.2.1.3 Modulazione BLD-PI

In questo caso il segnale ricevuto ha espressione
xPI(t) = √η(ap + m(t))cosω0t
dove η = Pma2p + Pm è pari all’efficienza della bld-pi introdotta al § 12.1.1.4, in modo da poter scrivere che la potenza del segnale ricevuto vale [688]   [688] Infatti, considerando nuovamente la portante in fase come un processo armonico indipendente da m(t) possiamo scrivere Px = η(a2p + Pm) ⋅ 1⁄2 = 1⁄2 ⋅  Pm dato che E{(ap + m(t))2} = a2p + Pm, in quanto E{ap ⋅ m(t)} = 0 qualora m(t) sia a media nulla. Px = 12 Pm, uguale ai due casi precedenti.
Per valutare l’SNRd, a numeratore della (14.93) non consideriamo l’intera potenza Pxc di xc(t) = √η(ap + m(t)), ma solo quella della sua componente utile u(t) = √ηm(t), che ha potenza Pu = ηPm = 2ηPx, mentre la potenza ηa2p si riferisce invece alla portante non modulata, e non trasporta informazione. Dato che per quanto riguarda il rumore demodulato siamo nella stessa condizione del caso am-bld ovvero Pνc = 2WN0, possiamo scrivere
SNRPI = PuPνc = 2ηPx2WN0 = η PxWN0 = η ⋅ SNR0
e dunque constatiamo che la presenza della portante comporta una riduzione di prestazioni in misura esattamente pari all’efficienza η = Pma2p + Pm.
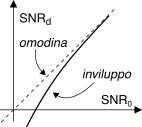
L’analisi esposta si riferisce però ad una demodulazione iq coerente, mentre per il caso bld-pi si usa il demodulatore di inviluppo (§ 12.2.5), che fornisce come risultato il modulo dell’inviluppo complesso ovvero
d(t) = |x(t) + ν(t)| = √[√η(ap + m(t)) + νc(t)]2 + ν2s(t)
figure f95.7.png
Finché |ν(t)| è piccolo e trascurabile rispetto ad ap, ci si ritrova approssimativamente nel caso precedente; al contrario per bassi valori di SNR0 la potenza utile Pu diviene una frazione di Px ancora più piccola di quanto non sia Pu = ηPm = 2ηPx, dando luogo ad un SNR peggiore del caso di demodulazione in fase e quadratura, come illustrato in figura.
 Sezione 14.1: Il rumore additivo nei segnali modulati Su Capitolo 14: Prestazioni delle trasmissioni modulate Sezione 14.3: Prestazioni della modulazione di frequenza