Consideriamo un segnale modulato x(t) ed affetto da un rumore additivo gaussiano bianco a media nulla n(t) (§ 8.4.2) con densità di potenza la cui occupazione spettrale è considerata costante a tutte le frequenze di interesse.

Prima ancora di essere demodulato il segnale ricevuto viene fatto passare attraverso un filtro di ricezione passa-banda H_R(f) centrato sulle frequenze del segnale, in modo da limitare la banda del rumore ricevuto e conseguentemente ridurre la potenza del rumore in ingresso al demodulatore. La risposta in frequenza H_R(f) del filtro ha modulo costante nella banda del segnale, e tende a zero al di fuori di essa, in modo che il segnale utile x(t) transita inalterato, mentre il rumore n(t) diviene limitato in banda, producendo l’uscita ν(t).

La qualità di ricezione (in funzione della frequenza) dipende dalla densità di potenza P_x(f) del segnale modulato e da quella P_ν(f) del rumore filtrato, in base al rapporto in cui P_x(f) dipende dal tipo di modulazione (cap. 12), mentre per quanto riguarda il rumore, dopo il filtraggio P_ν(f) risulta pari a D’altra parte, ha senso valutare l’SNR complessivo, ovvero il rapporto tra la potenza di segnale e quella di rumore totali: la prima risulta allora pari a mentre per quella di rumore dalla (14.89) si ottiene valutando cioè la potenza di rumore che attraversa il filtro di ricezione H_R(f).

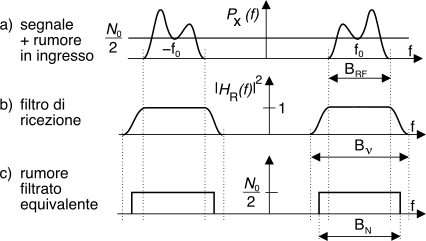
Definiamo questo concetto con l’aiuto della fig. 14.3, dove in alto è rappresentata la densità spettrale del segnale modulato, che occupa una banda [684]   [684] Il pedice _RF sta per radio frequency ed indica l’occupazione di banda a frequenze positive di un segnale modulato. B_RF. Nel caso fosse possibile adottare come filtro di ricezione un passa banda ideale (§ 13.1.2.1) si otterrebbe P_ν = N₀B_RF; invece H_R(f) presenta una regione di transizione (vedi fig. 14.3-b)) che ne accresce la banda ad un valore B_ν > B_RF. La potenza totale del rumore uscente da H_R(f) risulta pertanto pari a Il termine B_RF ≤ B_N ≤ B_υ rappresenta la cosiddetta banda di rumore definita come ossia come la banda di un filtro ideale equivalente che lascia passare la stessa potenza di rumore, come rappresentato in fig. 14.3-c).

Il rumore ν(t) in uscita dal filtro di ricezione H_R(f) è un processo ergodico bianco a media nulla di tipo passa-banda, e può quindi essere descritto nei termini delle sue componenti analogiche di bassa frequenza: Allo scopo di valutare la densità di potenza P_νc, νs(f) delle c.a. di b.f. di ν(t), facciamo riferimento alla figura 14.4 che a sinistra mostra la densità di potenza P_n(f) = N₀2 del rumore n(t) in ingresso ad un filtro di ricezione H_R(f) ideale e con risposta in frequenza unitaria |H_R(f₀)|² = 1; pertanto risulta e quindi dato che P⁺_ν(f) = P⁻_ν(−f) la (14.36) di pag. 1 fornisce Come discusso al § 11.4.4.2, ν_c(t) e ν_s(t) sono due processi congiuntamente gaussiani, ergodici, a media nulla ed incorrelati e pertanto statisticamente indipendenti in quanto gaussiani. Abbiamo inoltre verificato come presentino anche uguale varianza (e potenza), a sua volta uguale alla potenza del rumore filtrato P_ν, ovvero Il lato destro di fig. 14.4 rappresenta come nelle condizioni descritte la posizione di ν(t) nel piano dell’inviluppo complesso sia una v.a. bidimensionale a componenti gaussiane indipendenti e con identica d.d.p.; osserviamo inoltre che nel caso in cui la banda di ν(t) sia stretta rispetto a f₀, l’inviluppo complesso ν(t) = ν_c(t) + jν_s(t) evolve lentamente rispetto alla velocità di rotazione di ν(t)e ^jω₀t.

La quantità individua il parametro di sistema (o di riferimento) rispetto al quale confrontare l’SNR ottenuto per i tipi di modulazione discussi al cap. 12. La (14.91) è definita a partire dai valori delle condizioni operative, ovvero la potenza ricevuta P_x, il livello di rumore ^N₀⁄₂, e la massima frequenza W del segnale modulante; viceversa non dipende dai parametri di trasmissione, come l’indice di modulazione. In pratica SNR₀ corrisponde all’SNR in assenza di modulazione, ovvero ciò che si otterrebbe ricevendo direttamente il segnale di banda base con potenza P_x in presenza di rumore additivo P_N(f) = ^N₀⁄₂ attraverso un filtro passa basso con banda 2W.