14.4 Detezione di sinusoide nel rumore
Concludiamo questo capitolo con un argomento diverso dai precedenti: anziché calcolare l’
SNR dopo democulazione, affrontiamo il problema di decidere se nelle vicinanze di una determinata frequenza
f0 sia presente o meno un segnale
a banda stretta, ad esempio per effettuare una operazione di sintonizzazione automatica. A questo scopo torniamo ad occuparci della demodulazione
incoerente in fase e quadratura introdotta al §
12.2.4, ora applicata al problema di rilevare la presenza (o meno) di una sinusoide
s(t) immersa nel rumore entro una banda
BN, affrontato mediante il formalismo della
verifica di ipotesi (§
6.6.1) basata sul confronto tra il valore di una variabile di osservazione
ρ, che rappresenta il modulo dell’inviluppo complesso ricevuto, ed una soglia di decisione
λ, da posizionare a seconda del criterio adottato. Lo scopo è quello di arrivare ad una espressione per la d.d.p. di
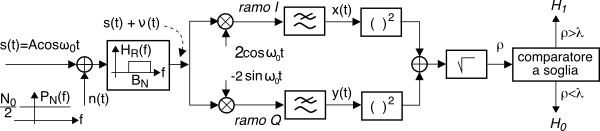
ρ a partire dalle uscite del demodulatore in fase e quadratura, secondo lo schema di fig.
14.14. Al §
16.6 verrà adottato uno schema simile, applicato al caso della trasmissione numerica.
14.4.1 Descrizione statistica del modulo dell’inviluppo complesso
Negli sviluppi che seguono scegliamo di indicare le uscite in fase e quadratura del demodulatore
iq rispettivamente come
x(t) e
y(t). Se in ingresso è presente il solo rumore
n(t),
x(t) e
y(t) corrispondono alle c.a. di b.f.
νc(t) e
νs(t) della sua versione filtrata; se invece in ingresso è presente anche
s(t) = Acosω0t, nell’uscita
x(t) del ramo in fase troviamo anche la
componente in fase di
s(t), pari ad
A, che diventa dunque il valor medio della v.a. estratta da
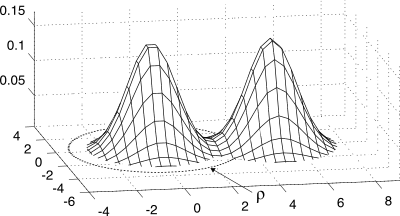
x(t). La fig.
14.15-a) rappresenta la d.d.p. delle v.a.
x ed
y estratte dai processi
x(t) e
y(t), mostrando anche le
curve di livello (vedi §
6.5) della gaussiana bidimensionale risultante.
Consideriamo ora che la sinusoide
s(t), quando presente, può in realtà avere una fase
φ qualsiasi, e dunque come discusso al §
13.1.2.3 il piano
(x, y) ruota dello stesso angolo
φ, causando la traslazione della d.d.p. bidimensionale della stessa quantità, come illustrato in fig.
14.15-b). Dunque la differenza tra quando
s(t) è presente o meno consiste nello
scostamento dall’origine del valor atteso della gaussiana, in qualsiasi direzione, e per questo in ingresso al comparatore di fig.
14.14 viene posta la grandezza
ρ = √x2 + y2, che è a sua volta una v.a., ed il cui valore viene rapportato alla soglia
λ.
Allo scopo di valutare la d.d.p. della v.a.
ρ ovvero del modulo dell’inviluppo complesso demodulato
z = x + jy e dunque poter individuare
λ secondo il criterio di massima verosimiglianza (§
6.6.2.1), applichiamo i risultati ottenuti al §
6.4.2 sulle trasformazioni di v.a. , in modo da passare dalla rappresentazione cartesiana
z = x + jy a quella polare
z = ρe jφ , come rappresentato in fig.
14.15-c). Definiamo dunque la trasformazione in oggetto, assieme alle rispettive funzioni inverse, come
e mostriamo che, nei due casi di segnale assente o presente, la v.a.
ρ assume rispettivamente la d.d.p. di
Rayleigh oppure quella di
Rice.
Variabile aleatoria di Rayleigh
In
assenza di segnale,
x ed
y sono due v.a. gaussiane
indipendenti
, a media nulla e uguale varianza
σ2, la cui d.d.p. congiunta si ottiene come prodotto delle d.d.p. marginali, e vale
La
pP, Φ(ρ, φ) viene quindi calcolata come prescritto dalla
(10.135) di pag.
1, valutando le espressioni per
pX, Y(x(ρ, φ), y(ρ, φ)) e
|J(x, y ⁄ ρ, φ)|, e ottenendo così
pP, Φ(ρ, φ) = ρ2πσ2 exp⎛⎝ − ρ22σ2⎞⎠ con ⎧⎨⎩ 0 < ρ < ∞ − π < φ < π
Le d.d.p. marginali
pP(ρ) e
pΦ(φ) si ottengono quindi saturando la d.d.p. congiunta rispetto all’altra variabile, in modo da ottenere
L’espressione di
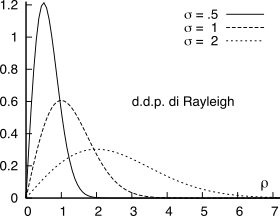
pP(ρ) in (
14.100) prende nome di d.d.p. di
Rayleigh, graficata in fig.
14.16, mentre il valor medio e la varianza della v.a.
ρ valgono rispettivamente
E’ inoltre possibile mostrare che per la v.a. di
Rayleigh vale la proprietà
Il valore
(14.102) può rappresentare la probabilità di
mancare un bersaglio per una distanza superiore a
λ, considerando gli errori di puntamento orizzontale e verticale entrambi gaussiani, indipendenti, a media nulla ed uguale varianza.
Variabile aleatoria di Rice
Consideriamo ora il caso in cui il tono
s(t) sia presente, e senza perdita di generalità assumiamo che abbia fase
φ = 0 in modo che la trasformazione (
14.98) possa ancora essere applicata considerando, al posto di
x, una v.a.
x’, sempre gaussiana con varianza
σ2, ma ora con media pari ad
A, ovvero la componente in fase di
s(t). In questo caso il prodotto tra le d.d.p. marginali si scrive come
e l’operazione di cambio di variabile porta alla d.d.p.
pP(ρ) detta di
Rice, che ha espressione
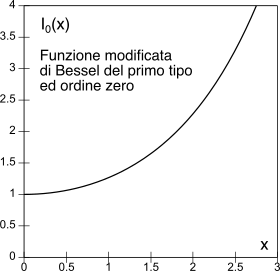
dove
I0(z) = 12π ∫2π0 ezcosφdφ è la funzione
modificata di Bessel
del primo tipo ed ordine zero, la cui espressione non ne permette il calcolo in forma chiusa, ma che può essere approssimata come
I0(z) ~ ez24 per
z≪1, e come
I0(z) ~ ez√2πz per
z≫1.
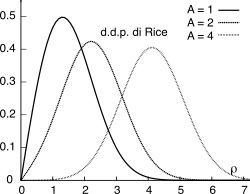
Nella parte sinistra di fig.
14.17 è mostrato l’andamento di
pP(ρ) con
σ = 1 e tre diversi valori di
A, in modo da poterlo confrontare con quello della seconda curva per la d.d.p. di Rayleigh alla fig.
14.16, ottenuta per lo stesso valore di
σ. Notiamo infine che per
A = 0 si torna al caso di Rayleigh, mentre per valori crescenti di
A l’andamento della d.d.p. di Rice approssima sempre più quello di una gaussiana. Nella parte a destra di fig.
14.17 sono invece raffigurate le gaussiane bidimensionali che danno luogo alle distribuzioni di Rayleigh e di Rice.
14.4.2 Detezione incoerente di sinusoide nel rumore
Come fatto osservare nella discussione di fig.
14.15, se il segnale
s(t) si presenta con una fase
φ ≠ 0 ovvero
s(t) = Acos(ω0t + φ), il piano dell’inviluppo complesso ruota dello stesso angolo, ed è per questo motivo che abbiamo scelto il
modulo ρ dell’inviluppo complesso come grandezza su cui operare la decisione, di cui abbiamo trovato la d.d.p. per i casi di segnale assente e presente.
Compromesso tra banda di ricerca e probabilità di detezione
Prima di procedere osserviamo che qualora la frequenza di
s(t) fosse pari a
f = f0 + Δf, l’inviluppo complesso
z = x + jy ruoterebbe con velocità angolare
2πΔf, ma il suo modulo
ρ resterebbe costante e pari ad
A, dando luogo anche in questo caso alla d.d.p. di Rice. Ciò consente l’adozione dello schema di fig.
14.14 per la ricerca di una sinusoide che cade entro
tutta la
BN del filtro di ingresso; d’altra parte, all’aumentare di
BN aumenta anche la potenza
σ2 del rumore, causando come vedremo tra breve un peggioramento delle prestazioni del decisore.
Analizziamo i risultati fin qui ottenuti nell’ottica della decisione di ipotesi statistica (§
6.6.1), allo scopo di definire il criterio con cui scegliere la soglia di decisione
λ da utilizzare nello schema di fig.
14.14.
Il caso di segnale assente (in cui la v.a. di osservazione
ρ ha d.d.p. di Rayleigh) viene quindi indicato come
ipotesi H0, mentre quello in cui
s(t) è presente
ipotesi H1 (e
ρ ha d.d.p. di Rice). In entrambi i casi la dinamica dei valori di
ρ è direttamente legata (attraverso le
(14.100) e
(14.104)) alla potenza di rumore in ingresso
σ2 = N0BN, pari a quella delle c.a. di b.f.
νc(t) e
νs(t), mentre per quanto riguarda il valor medio di
ρ, nell’ipotesi
H0 si ha
mρ = σ√π2 (eq.
(14.100)), e per
H1 risulta
mρ → A quando
A ≫ σ.
Decisione di massima verosimiglianza
In figura
14.18 oltre alle d.d.p. condizionate alle ipotesi
p(ρ ⁄ H0) e
p(ρ ⁄ H1) e calcolate per
σ = 1 ed
A = 4, viene mostrato anche il valore
λML per cui esse si intersecano ovvero
p(ρ ⁄ H0)|ρ = λML = p(ρ ⁄ H1)|ρ = λML, e la regola di decisione
p(ρ ⁄ H1)p(ρ ⁄ H0) H1 ≷ H0 1 che ne consegue corrisponde al criterio di massima verosimiglianza (§
6.6.2.1), attuato nella forma
ρλML H1 ≷ H0 1 ovvero
ρ H1 ≷ H0 λML.
A seguito della decisione si possono verificare i due tipi di evento di errore
- falso allarme con probabilità Pr(e ⁄ H0) = ∫∞λ p(ρ ⁄ H0) dρ = Pfa
- perdita con probabilità Pr(e ⁄ H1) = ∫λ0 p(ρ ⁄ H1) dρ = Pp
rispettivamente pari alle aree colorate in celeste e giallo di fig.
14.18. Osserviamo quindi che la scelta
λ = λML risulta
ottima qualora non sussistano
costi per i due tipi errori
Pfa e
Pp (vedi sotto), e le probabilità
a priori di
H0 ed
H1 siano uguali. Infatti in tal caso la probabilità di errore complessiva
risulta
minima, dato che spostando
λ a destra o sinistra rispetto a
λML, una delle due aree aumenta più di quanto non diminuisca l’altra.
Calcolo della soglia Tutto bello, ma volendo ottenere il valore di
λML, come si fa? La condizione che per
ρ = λML risulti
p(ρ ⁄ H0) = p(ρ ⁄ H1) comporta l’uguaglianza tra le d.d.p. di Rayleigh
(14.100) e di Rice
(14.104), ovvero
ρσ2 exp⎛⎝− ρ22σ2⎞⎠ = ρσ2 exp⎛⎝− ρ2 + A22σ2⎞⎠ I0⎛⎝ρAσ2⎞⎠
da cui con alcuni passaggi si ottiene
exp⎛⎝A22σ2⎞⎠ = I0⎛⎝ρAσ2⎞⎠
Una volta noti i valori di
A e
σ il primo membro è un numero, e dunque per via numerica si trova il valore di
λML = ρ che rende il secondo membro pari al primo.
Qualora si conoscano i valori di
Pr(H0) e
Pr(H1) e questi siano diversi da
1⁄2, ponendo
λ = λML la
(14.105) non è più minimizzata. In tal caso la soglia ottima viene invece stabilita secondo il criterio di
massima probabilità a posteriori o
map, vedi §
17.1.2, ovvero scegliendo l’ipotesi
Hi la cui probabilità
a posteriori p(Hi ⁄ ρ) è massima. Applicando il teorema di Bayes (§
6.1.4) si ottiene
p(Hi ⁄ ρ) = p(ρ ⁄ Hi)Pr(Hi)p(ρ) e dunque la regola di decisione diviene
che nel caso di ipotesi equiprobabili
Pr(H0) = Pr(H1) degenera nel criterio di
ml.
Allarghiamo ora il campo di applicazione della decisione statistica a situazioni in cui può essere associato un differente
costo ai due tipi di errore, così come si può associare un
guadagno all’evento di decisione corretta (o
detezione)
la cui probabilità
Pd = ∫∞λp(ρ ⁄ H1)dρ è misurata dall’area
verde in fig.
14.18. Ad esempio, nell’ambito del
telerilevamento si tenta di massimizzare la probabilità di detezione a spese di quella di falso allarme, mentre in
campo medico si tende a preferire un falso allarme, piuttosto che trascurare l’importanza di un sintomo o referto. In questi casi nella
14.106 compare un altro termine che tiene conto dei costi associati alla decisione, in modo da preferire uno dei due tipi di errore rispetto all’altro.
Criterio di Neyman-Pearson
In alcuni casi la probabilità a priori Pr(H1) che il segnale sia presente non è nota in quanto l’evento è di natura sporadica, e noi lì, in attesa che si verifichi. Un possibile approccio è allora quello di fissare la Pfa massima tollerata, e quindi tentare di massimizzare la prob. di detezione Pd, come avviene adottando il criterio di Neyman-Pearson, sulla cui descrizione non ci addentriamo.
Torniamo ad investigare sulla applicazione del criterio di massima verosimiglianza, la cui soglia di decisione λML può essere fissata una volta nota l’ampiezza A della sinusoide e la deviazione standard σ del rumore; a volte però tali grandezze non sono note, se non a grandi linee!
In particolare, qualora sia noto solamente che
A⁄σ≫1 e dunque in presenza di una ampiezza
A ≳ 10σ ben maggiore della dinamica del rumore, notiamo che all’aumentare di
Aσ le curve di fig.
14.18 si allontanano ma non cambiano larghezza, ed il valore di
λML si avvicina (da destra) ad
A2. Ponendo quindi
λ = A2 e sostituendo le espressioni di Rayleigh (
14.100) e di Rice (
14.104) per le d.d.p. condizionate in quella (
14.105) della
Pe, otteniamo
Per ciò che riguarda il primo termine, applicando il risultato (
14.102) si trova il valore
∞⌠⌡A2 ρσ2 exp⎛⎝− ρ22σ2⎞⎠ dρ = exp⎛⎝− A28σ2⎞⎠
Per il secondo termine, osserviamo che il suo valore è ben più piccolo del primo (si veda la figura
14.18 tracciata per
A = 4, o le considerazioni riportate al §
14.5.1), e quindi può essere trascurato, fornendo in definitiva
per
Aσ ≫ 1. Ricordando ora che
A22 rappresenta la potenza della sinusoide, e che
σ2 è la potenza del rumore, il risultato trovato ha una immediata interpretazione in termini di
SNR = A2 ⁄ 2σ2: