Prestazioni della modulazione di frequenza

Prev Sezione 14.2: Prestazioni delle trasmissioni AM Su Capitolo 14: Prestazioni delle trasmissioni modulate Sezione 14.4: Detezione di sinusoide nel rumore Next

14.3 Prestazioni della modulazione di frequenza

Occupiamoci ora della valutazione dell’SNR dopo demodulazione per il caso di una trasmissione fm (§ 12.3), analizzando come esso dipenda dalle condizioni di ricezione (potenza ricevuta P_x, densità di potenza del rumore ^N₀⁄₂ e banda del ricevitore B_N) e dai parametri di trasmissione (indice di modulazione β e banda del segnale modulante W). Anticipiamo che la natura non lineare della modulazione fm porterà a sviluppi del tutto diversi dal caso dell’am, infatti troveremo che se la potenza del rumore in ingresso al ricevitore non è eccessiva

quando la potenza del segnale ricevuto P_x aumenta, quella del segnale demodulato resta costante, mentre invece diminuisce quella del rumore dopo demodulazione;
l’SNR dopo demodulazione migliora all’aumentare della banda occupata.

Per arrivare a questi risultati non banali, valutiamo innanzitutto ciò che accade nella ricezione di una portante non modulata, e quindi analizziamo come lo scenario si modifica in presenza di segnale. Infine, illustriamo i motivi che determinano il rapido degrado di prestazioni nel caso di rumore elevato.

14.3.1 Rumore dopo demodulazione FM

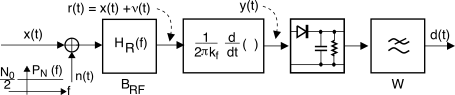
L’analisi viene svolta considerando un demodulatore a discriminatore (§ 12.3.2.2)

Demodulatore FM a discriminatore

alla cui uscita r(t) del filtro di ricezione è presente una portante non modulata x(t) di ampiezza [689] [689] Con questa posizione, la potenza della portante risulta (√2 P_x)²2 = 2 P_x2 = P_x. A = √2P_x, oltre che un rumore gaussiano bianco limitato in banda ν(t), ovvero

r(t) = A cosω₀t + ν_c(t) cosω₀t − ν_s(t) sinω₀t

La banda del filtro H_R(f) (e dunque di ν(t)) deve essere sufficiente a far passare le frequenze che sarebbero presenti se la portate fosse modulata, e che nel caso fm può essere stimata applicando la regola di Carson (eq. 14.56), ossia B_RF = B_C ≃ 2W(β + 1).

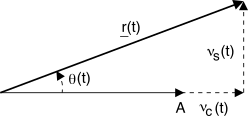
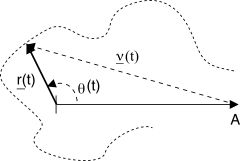
In presenza di una portante non modulata, le componenti analogiche di bassa frequenza dell’inviluppo complesso r(t) del segnale ricevuto

(14.94) r(t) = r_c(t) + jr_s(t) sono espresse come ⎧⎨⎩ r_c(t) = A + ν_c(t) r_s(t) = ν_s(t)

di cui a fianco è rappresentata la costruzione vettoriale: r_c(t) è la somma tra l’ampiezza A della portate ed una v.a. ν_c(t) gaussiana a media nulla e deviazione standard σ = √N₀B_N ≥ √N₀B_RF , mentre r_s(t) consiste in un’altra v.a. ν_s(t) della stessa natura di ν_c(t) ma ad essa incorrelata [690] [690] Si veda il § 14.4.1 per una analisi più approfondita degli aspetti statistici della questione, che portano a definire ρ = |r(t)| una v.a. di Rice..

Ricordando ora che nel caso fm il segnale informativo è legato alla derivata della fase θ(t) di r(t), esprimiamo r(t) mettendo θ(t) in evidenza

r(t) = ℜ{r(t)e^jω₀t} = ℜ{|r(t)|e^jθ(t)e^jω₀t} = |r(t)|cos(ω₀t + θ(t))

in cui possiamo considerare il termine |r(t)| rimosso dal limitatore (vedi § 12.3.2.2) che usualmente è anteposto al discriminatore. Il segnale y(t) in uscita dal derivatore è quindi descritto (a parte il segno) come

y(t) = 12πk_f ddt r(t) ⇒ 12πk_f ddt cos(ω₀t + θ(t)) = = ⎛⎜⎝f₀k_f + 12πk_f ddtθ(t)⎞⎟⎠ sin(ω₀t + θ(t))

e viene a sua volta elaborato da parte del demodulatore di inviluppo come fosse un segnale bld-pi (§ 12.1.1.2), fornendo in definitiva un segnale demodulato dovuto al solo rumore

(14.95) d(t) = 12πk_f ddt θ(t) = ν_d(t)

14.3.2 Caso di basso rumore

Con riferimento all’ultima figura, osserviamo che qualora P_x = A²2 ≫ σ²_{ν_c} = σ²_{ν_s} = N₀B_N i valori di ν_c(t) e ν_s(t) risultano piccoli rispetto ad A, e l’inviluppo complesso ricevuto r(t) rimane prossimo a quello della portante non modulata, dato che in questo caso ν(t) ha modulo abbastanza più piccolo di A. L’angolo θ(t) che compare nella (14.95) può dunque essere approssimato come

θ(t) = arctan ν_s(t)A + ν_c(t) ≃ arctan ν_s(t)A ≃ ν_s(t)A

la cui densità spettrale di potenza vale

(14.96) P_θ(f) = 1A² P_{ν_s}(f) = N₀A²

in quanto P_{ν_s}(f) = N₀ come discusso al § 14.1.3. Ricordiamo ora (vedi § 3.6) che l’operazione di derivata svolta dal discriminatore equivale a moltiplicare lo spettro di ampiezza del segnale in ingresso per j2πf, ovvero moltiplicare la sua densità di potenza per (2πf)²: applichiamo questo risultato per ottenere la densità di potenza di ν_d(t) (14.95) a partire dalla (14.96), in modo che la densità di potenza del rumore demodulato ν_d(t) risulti

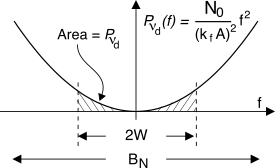
P_{ν_d}(f) = 1(2πk_f)² (2πf)² P_θ(f) = ⎛⎝fk_f⎞⎠² N₀A² = N₀(k_fA)² f²

e quindi la relativa potenza totale P_{ν_d} = σ²_{ν_d} si calcola come

(14.97) P_{ν_d} = ^∞⌠⌡_−∞P_{ν_d}(f)df = 2 ^W⌠⌡₀N₀(k_fA)² f²df = = 2 N₀(k_fA)² ⋅ f³3 ||^W₀ = 23 N₀(k_fA)² W³

in cui W è la banda del segnale modulante (se ci fosse), ed il rumore è limitato in tale banda in virtù del filtro passa basso posto a valle del discriminatore [691] [691] Si noti che le potenze σ²_{ν_c} e σ²_{ν_s} delle c.a. di b.f. del rumore in ingresso al discriminatore sono invece relative alla banda B_N, ≥ di quella B_RF del segnale modulato..

Notiamo subito la veridicità della prima affermazione fatta ad inizio sezione: la potenza complessiva del rumore dopo demodulazione fm diminuisce all’aumentare della potenza del segnale ricevuto P_x = A²2. Una seconda osservazione molto importante è che, per effetto della derivata, la densità di potenza del rumore demodulato ha un andamento parabolico.

Segnale presente

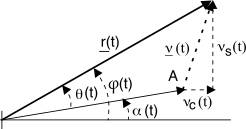
Continuando nell’ipotesi di basso rumore ovvero P_x = A²2 ≫ σ²_{ν_c} = σ²_{ν_s} = N₀B_N, possiamo osservare che (vedi fig. a lato) la presenza di una fase

modulante α(t) nel segnale

x_FM(t) = Acos(2πf₀t + α(t))

comporta che la fase φ(t) dell’inviluppo complesso del segnale ricevuto r(t) è costituita dalla somma tra α(t) e l’angolo θ(t) dovuto al rumore sovrapposto alla portante di ampiezza A, cioè φ(t) = α(t) + θ(t). Pertanto l’uscita (14.95) del discriminatore diviene

d(t) = 12πk_f ddt α(t) + 12πk_f ddt θ(t) = s_d(t) + ν_d(t)

ed il rapporto tra le potenze dei due termini definisce l’SNR dopo demodulazione come SNR_d = P_{s_d}P_{ν_d}, dove quindi P_{s_d} è la potenza di segnale utile demodulato s_d(t) = 12πk_f ddtα(t), e P_{ν_d} è la potenza del rumore demodulato calcolata alla (14.97).

Ricordando (§ 11.2.2) che α(t) = 2πk_f ∫^t_−∞m(τ)dτ, per la potenza di s_d(t) si ottiene [692] [692] Dato che gli operatori di derivata ed integrale si annullano, ovvero P_{s_d} = Pot⎧⎩12πk_f ddtα(t)⎫⎭ = Pot⎧⎩12πk_f ddt2πk_f ∫^t_−∞m(τ)dτ⎫⎭ = Pot{m(t)} = P_m. In definitiva, abbiamo semplicemente demodulato! P_{s_d} = P_m = ∫^W_− WP_m(f)df, e quindi

SNR_d = P_{s_d}P_{ν_d} = P_m23 N₀(k_fA)²W³ = 3 P_mk²_fW²N₀W A²2 = 3 σ²_{f_d}W² P_xN₀W = 3 β² SNR₀

avendo sostituito P_mk²_f con σ²_{f_d} (vedi sotto), A²2 con la potenza della portante ricevuta P_x, σ_{f_d}W con l’indice di modulazione β (§ 12.3.3.4), e P_xN₀W con l’SNR di sistema SNR₀ (§ 14.1.4). Il risultato ottenuto conferma la seconda affermazione di inizio sezione: si ha un miglioramento rispetto all’SNR₀ (e dunque rispetto all’am) tanto maggiore quanto maggiore è la banda occupata dal segnale modulato B_RF ≃ 2W(β + 1) (eq. (14.56) a pag. 1), ovvero quanto più è grande l’indice di modulazione β.

Discussione dei passaggi

Per mostrare che P_mk²_f = σ²_{f_d}, indichiamo con f_d(t) = f_i(t) − f₀ la deviazione della frequenza istantanea f_i(t) (§ 12.3) rispetto a quella della portante f₀. Ricordiamo quindi che f_i(t) = 12π ddt ψ(t) in cui ψ(t) è la fase istantanea ψ(t) = 2πf₀t + α(t), e dato che per l’fm α(t) = 2πk_f ∫^t_−∞m(τ)dτ si ottiene

f_d(t) = 12π ddt⎛⎜⎝2πf₀t + 2πk_f^t⌠⌡_−∞m(τ)dτ⎞⎟⎠ − f₀ = f₀ + k_fm(t) − f₀ = k_fm(t)

Pertanto si ha σ²_{f_d} = k²_fσ²_m = k²_fP_m se m(t) è a media nulla: praticamente, σ_{f_d} rappresenta la deviazione standard della frequenza istantanea, e per questo è una grandezza proporzionale alla larghezza di banda del segnale modulato [693] [693] Infatti, il rapporto σ_{f_d}W definito al § 12.3.3.4 come indice di modulazione β_p, rappresenta appunto una misura del rapporto tra l’occupazione di banda efficace del segnale modulato, e la massima frequenza W presente nel segnale modulante.. D’altra parte, questo risultato è un aspetto della conversione am-fm che avviene per alto indice di modulazione, come descritto al § 12.3.3.3.

Discussione del risultato

Notiamo innanzitutto che se β < 1√3 ≃ 0, 58 il valore di SNR = 3β²SNR₀ non aumenta affatto, anzi le prestazioni peggiorano. Ma con bassi indici di modulazione abbiamo già visto (§ 12.3.3.1) che l’fm ha un comportamento che può avvicinarsi a quello lineare dell’am, e dunque ci possiamo non-sorprendere. D’altra parte, SNR può migliorare (e di molto) con β > 1√3: se ad esempio β = 5 si ottiene 3β² = 75 volte meglio, ovvero 17,75 dB di miglioramento! In compenso, la regola di Carson ci dice che la banda occupata aumenta di circa 2(β + 1) = 12 volte quella di banda base... dunque il miglioramento di SNR [694] [694] Miglioramento che può essere sfruttato quando ad esempio il collegamento è di tipo punto-punto, come nel caso di un ponte radio con antenne direttive od una comunicazione satellitare, in modo da contenere la potenza irradiata entro il cono di emissione e non invadere lo spettro radio riservato ad altre trasmissioni. avviene a spese dell’occupazione di banda, e pertanto costituisce una manifestazione del compromesso banda-potenza, vedi pagg. 1 e 1.

Verrebbe ora quasi il desiderio di aumentare indefinitamente β (nei limiti della banda disponibile) per migliorare a piacere l’SNR. Peccato non sia possibile, dato che ad un certo punto l’analisi effettuata perde validità: infatti, aumentando β anche la banda di rumore del ricevitore deve crescere, essendo aumentata la banda del segnale modulato. Pertanto le condizioni P_x = A²2 ≫ σ²_{ν_c} = σ²_{ν_s} = N₀B_N non sono più verificate, con le conseguenze illustrate di seguito.

14.3.3 Caso di elevato rumore

Qualora il valore efficace del rumore in ingresso al discriminatore sia confrontabile con quello del segnale utile ricevuto si verifica un effetto soglia,

ed all’aumentare del rumore l’SNR degrada molto rapidamente. Per indagarne le cause facciamo riferimento allo schema a lato, che mostra l’inviluppo complesso della portante non modulata A, del rumore in ingresso ν(t), e del segnale ricevuto r(t), notando che se i valori efficaci dei primi due sono comparabili, può verificarsi il caso che r(t) ruoti attorno all’origine. Quando ciò si verifica, a valle del derivatore che è presente nel discriminatore si determina un click, ovvero un segnale impulsivo di area pari a 2π, come illustrato alla figura 14.13-a. Questo fatto è facilmente verificabile, ascoltando una radio fm broadcast, che in condizioni di cattiva ricezione manifesta la comparsa di un rumore, appunto, impulsivo.

Figure 14.13 a) - Rumore impulsivo dopo demodulazione fm; b) - effetto soglia

All’aumentare della potenza di rumore, aumenta la frequenza con la quale r(t) “aggira” l’origine, e pertanto aumenta la frequenza dei click, che tendono a produrre un crepitìo indistinto. Si è trovato che questo effetto si manifesta a partire da un SNR₀ di sistema inferiore [695] [695] L’effetto soglia interviene prima per i valori di β più elevati, vedi fig. 14.13-b. a 10-25 dB, e per valori SNR₀ minori di tale valore l’effetto aumenta molto rapidamente, cosicché si parla di effetto soglia. Le curve di 14.13-b riportano un tipico andamento dell’SNR dopo demodulazione, con l’indice β che svolge il ruolo di parametro, e possiamo osservare come con un SNR₀ inferiore alla soglia le prestazioni degradino rapidamente. Si è trovato che demodulando con un PLL, anziché con un discriminatore, il valore di soglia si riduce di circa 3 dB.

Nella pratica comune il segnale di rumore può essere costituito da una interferenza dovuta ad una emittente adiacente (ossia con una portante prossima a quella della emittente sintonizzata) che sovramodula, ovvero adotta un indice di modulazione troppo elevato, ed invade la banda delle emittenti contigue.

Esercizio

Sia dato un trasmettitore FM con potenza trasmessa 1 Watt e segnale modulante m(t) con banda ± W = ±10 MHz. Un collegamento con attenuazione disponibile A_d = 100 dB lo interfaccia ad un ricevitore con temperatura di sistema T_ei = 2900 ^oK. Desiderando un SNR = 40 dB, calcolare:

1) Il fattore di rumore del ricevitore in dB;

2) Il minimo valore dell’indice di modulazione e la banda occupata a radiofrequenza B_RF;

3) Se il valore di β trovato in 2) non sia troppo piccolo, e quale sia il suo massimo valore;

4) Il nuovo valore β’, volendo dotare il collegamento di un margine pari a 25 dB.

Soluzione

1) Questa domanda va affrontata dopo lo studio del § 18.2, dove è mostrato che T_{e_i} = T₀(F − 1) + T_g = T₀F se T_g = T₀; assumiamo quest’ipotesi per vera e dunque F = T_{e_i}T₀ = 10; pertanto F_dB = 10 dB. Per proseguire l’esercizio con le nozioni fin qui acquisite, esplicitiamo che
P_n(f) = N₀2 = 12kT_ei = 12 ⋅ 1.38 ⋅10^− 23 ⋅ 2900 ≃ 2 ⋅ 10^− 20 Watt/Hz.

2) Qui è utilizzata la relazione W_R = W_TG_d dal § 19.1, in modo da scrivere
SNR = 3β²SNR₀ = 3β²W_RN₀W = 3β²W_TG_dN₀W;
il valore numerico di SNR risulta 10^SNR_dB10 = 10⁴, mentre quello di A_d è 10^A_d(dB)10 = 10¹⁰ e quindi G_d = 1 ⁄ A_d = 10^− 10. Sostituendo i valori, ed invertendo la relazione, si ottiene
β_min = √SNR ⋅ N₀W3 ⋅ W_TG_d = √10⁴ ⋅ 4 ⋅10^− 20 ⋅ 10⁷3 ⋅ 10^− 10 = 3.65
Applicando la regola di Carson per la banda:
B_RF ≃ 2W ⋅ (β + 1) = 2 ⋅ 10⁷ ⋅4.65 = 9.3 ⋅ 10⁷ = 93 MHz.

3) La validità dei risultati 2) dipende dal verificarsi delle condizioni di basso rumore, ovvero deve risultare
W_R ≫ σ²_{ν_c} = σ²_{ν_s} = N₀B_N = N₀B_RF = 4 ⋅ 10^− 20 ⋅ 9.3 ⋅10⁷ = 3.72 ⋅ 10^− 12 Watt,
ma poiché W_R = W_TA_d = 110¹⁰ = 10^− 10, si ha W_Rσ²_{ν_c} = 10^− 103.72 ⋅ 10^− 12 = 26, che soddisfa abbastanza bene l’esigenza di basso rumore. Per trovare β_Max partiamo dal vincolo che debba risultare
W_R ≥ 10 ⋅ σ²_{ν_c} = 10 ⋅ N₀ ⋅ B_RF = 10 ⋅ N₀ ⋅2W ⋅ (β_Max + 1)
da cui otteniamo
β_Max = W_R10 ⋅ N₀ ⋅2W − 1 = 10^− 108 ⋅ 10^− 12 − 1 = 12.5 − 1 = 11.5
al quale corrisponde una banda
B_RF = 2W ⋅ (β_Max + 1) = 2 ⋅ 10⁷ ⋅12.5 = 250 MHZ,
ed un guadagno di SNR = 10lg₁₀3β²_Max ≃ 26 dB, mentre con β_min nominale si sarebbe ottenuto 10lg₁₀(3 ⋅ 3.65²) = 16 dB.

4) Il concetto di margine è introdotto al § 19.1; un margine di 25 dB equivale a far fronte ad una attenuazione supplementare A_d’ = 10^2.5 = 316 volte. Proviamo ad ottenere lo stesso SNR con un nuovo valore
β’: SNR = 10⁴ = 3β’² W_TG_dG_d’N₀W = 3β²W_TG_dN₀W β’²β²G_d’ ;
dunque deve risultare β’²β² G_d’ = 1 e quindi
β’² = β²√1G_d’ = 3.65√316 = 3.65 ⋅ 17.7 = 64.88
.... non ce la facciamo. Infatti, al più (con β = β_Max = 11.5) si ha un margine di 10 dB.

14.3.4 Enfasi e de-enfasi

Abbiamo osservato che in presenza di rumore bianco in ingresso, il rumore dopo demodulazione ha un andamento parabolico. Questo comporta che, se il messaggio modulante m(t) avesse una densità spettrale P_m(f) a sua volta bianca, l’SNR(f) alle frequenze più elevate sarebbe molto peggiore del suo valore per frequenze inferiori. Nella pratica, si possono verificare (ad esempio) i seguenti problemi:

Nelle trasmissioni fdm-fm (vedi § 11.1.1.2), in cui più canali vengono modulati am-blu, multiplati in frequenza, e ri-modulati congiuntamente in fm a basso indice, i canali agli estremi della banda fdm sono più rumorosi;
nell’fm broadcast (vedi § 25.2), il segnale modulante è molto più ricco di energia alle basse frequenze, dunque il problema del rumore elevato in alta frequenza è aggravato dal “basso segnale”.

Il rimedio a tutto ciò consiste nel modificare m(t) mediante un circuito detto di enfasi, in quanto il suo ruolo è quello di enfatizzare le frequenze più elevate. In tal modo anche m(t) presenta uno spettro parabolico e l’SNR sarà lo stesso a tutte le frequenze! L’alterazione introdotta su m(t) viene quindi rimossa mediante una rete di de-enfasi posta in ricezione (praticamente un integratore, ovvero un passa-basso) tale da ripristinare l’originale sagoma spettrale del segnale, rendendo la densità di potenza del rumore costante in frequenza.

Con un po’ di riflessione, ci si accorge che l’uso di una coppia enfasi-deenfasi equivale ad effettuare una trasmissione a modulazione di fase (vedi pag. 1). In realtà, la rete di enfasi non è un derivatore perfetto (altrimenti annullerebbe le componenti del segnale a frequenza prossima allo zero), ed esalta le frequenze solo se queste sono maggiori di un valore minimo. Pertanto, si realizza un metodo di modulazione “misto”, fm in bassa frequenza e pm a frequenze (di messaggio) più elevate.

Prev Sezione 14.2: Prestazioni delle trasmissioni AM Su Capitolo 14: Prestazioni delle trasmissioni modulate Sezione 14.4: Detezione di sinusoide nel rumore Next