Gli aspetti accennati sono immediatamente applicabili a segnali di natura analogica, definiti per tutti gli istanti di tempo, e che assumono valori nell’ambito dei numeri reali (o, come vedremo al cap. 11, complessi), come ad esempio nel caso di un segnale audio (vocale o musicale); d’altra parte, un segnale può viceversa essere definito solo per istanti di tempo discreti ovvero numerabili, ed assumere valori anch’essi discreti, come ad esempio per i documenti conservati su di un computer. In tal caso il segnale viene detto sequenza numerica, e la sua trasmissione coinvolge ulteriori elementi.

Corrisponde all’andamento nel tempo di una grandezza fisica s(t), di natura elettromagnetica come nei campi dell’elettronica o dei circuiti, ovvero risultato della trasduzione elettrica di grandezze di altra natura, come nel caso di un segnale audio che consiste in un’onda trasversale di pressione-velocità convertita in una tensione da un microfono, o nel caso di una misura di posizione, velocità od accelerazione ottenuta mediante tecniche di geo-localizzazione come nel telerilevamento, oppure ancora acquisita mediante sensori utilizzati ad es. nel contesto dei sistemi di controllo automatico.

Un fondamentale strumento per lo studio di un segnale s(t) è la sua analisi spettrale, condotta per mezzo di una particolare trasformazione lineare, che individua un corrispondente segnale (in generale complesso) S(f) funzione di una diversa variabile indipendente f nota come frequenza. Questo nuovo segnale è un sorta di radiografia, una analisi che individua lo spettro di frequenze di cui è costituito s(t); la differenza tra la minima e massima delle frequenze presenti è detta banda del segnale, uno dei principali parametri che lo caratterizzano dal punto di vista dell’impegno delle risorse necessarie a trasmetterlo.

L’attraversamento di un canale da parte di un segnale analogico, che come discusso al § 1.1 avviene grazie ad un mezzo trasmissivo, viene studiato mediante l’ausilio di alcuni strumenti fondamentali qui brevemente descritti, e ripresi al § 1.6.

Qualora il canale (o filtro) attraverso cui convogliare il segnale s(t) non permetta l’attraversamento alle frequenze in esso presenti, come ad esempio nel caso di un collegamento radio, occorre trasformare il segnale mediante una tecnica chiamata modulazione, in modo che il risultato giaccia in una banda di frequenze compatibile con la risposta in frequenza del canale. Il segnale modulato occupa ora una banda concentrata attorno ad un frequenza più elevata detta portante, ed il suo andamento nel dominio del tempo è descritto da un segnale noto come inviluppo complesso.

Nel caso di collegamenti a distanza il mezzo trasmissivo attenua il segnale in transito, che viene ricevuto con una ampiezza molto inferiore a quella di trasmissione. Pertanto è fondamentale verificare che la potenza ricevuta non sia inferiore alla soglia di sensibilità del ricevitore, ovvero il minimo segnale necessario a garantire la qualità di ricezione richiesta. D’altra parte, attenuazioni e distorsioni di entità non trascurabile possono verificarsi anche in assenza di collegamenti a distanza, qualora si verifichi un disadattamento di impedenza tra stadi della catena trasmissiva.

Quando il contenuto informativo è costituito da una sequenza numerica s_n i suoi elementi possono essere messi in relazione biunivoca con un più generale alfabeto simbolico A a cardinalità finita, come ad esempio nel caso di un testo scritto, in cui A è il vero e proprio alfabeto della lingua in cui è scritto il testo. In questo caso sorgente e destinazione della trasmissione sono anch’esse indicate come numeriche, mentre gli elementi della sequenza s_n sono indicati come simboli, emessi dalla sorgente ad intervalli temporali regolari distanziati da un tempo di T_s secondi detto periodo di simbolo, il cui inverso f_s = ¹⁄_Ts è indicato come frequenza di simbolo [15]   [15] Una sequenza prodotta da una sorgente numerica si presta facilmente ad essere trasformata in un’altra, con un diverso alfabeto ed una differente frequenza di simbolo. Per fissare le idee, consideriamo i simboli di una sequenza numerica s_n ad L valori (ovvero A = 1, 2, ⋯, L): questi possono essere presi a gruppi di M, producendo nuovi simboli q_k a velocità M volte inferiore, ma con L^M valori distinti. Se si dispone di un alfabeto di uscita ℬ ad H valori (ovvero ℬ = 1, 2, ….H), i gruppi di M simboli L-ari originari possono essere rappresentati con gruppi di N simboli H-ari purché L^M ≤ H^N. Esempio: per codificare in binario (H = 2) simboli con L = 26 valori, occorrono almeno N = 5 bit/simbolo, ottenendo così 2⁵ = 32 > L = 26. E’ un ragionamento confuso? Si e no. Basta fare degli esempi.. 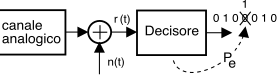Ciò che permette la trasmissione tra sorgente e destinazione dell’informazione contenuta nel messaggio prende ora il nome di canale numerico , pensabile come una entità a sé stante, che la figura seguente mostra essere comunque costituito al suo interno dal canale analogico già discusso, e basato a sua volta su di un mezzo trasmissivo.

Denota il dispositivo che provvede a generare un segnale analogico s(t) in grado di trasportare l’informazione espressa dalla sequenza numerica s_n, e la cui etimologia deriva dalla contrazione di modulatore e demodulatore, mentre il termine codificatore di linea è riferito alla trasmissione su di una linea di trasmissione come ad esempio un collegamento in cavo. In particolare, una trasmissione unidirezionale [16]   [16]  Nelle trasmissioni unidirezionali, sorgente e destinazione non si scambiano i ruoli. La trasmissione stessa viene anche indicata con il termine di half-duplex. necessita di solo metà delle funzioni del modem per entrambi i lati del collegamento, mentre nel caso di collegamento full duplex (in cui gli estremi del canale possono essere contemporaneamente sorgente e destinazione) il modem opera allo stesso tempo nelle due direzioni.

Quando il decisore presente nel modem produce un simbolo diverso da quello trasmesso si verifica un errore, e la frazione del numero di eventi di errore rispetto al totale rappresenta la probabilità di errore, il cui valore costituisce il parametro che caratterizza la qualità del collegamento numerico. Evidentemente il valore della probabilità di errore è strettamente legato in modo inverso a quello del rapporto segnale-rumore snr che si riscontra per il canale analogico sottostante.

Consiste nell’invio di più simboli di quanti non ne produca la sorgente, e quindi di fatto aumentando il loro numero per unità di tempo, che da f_s passa ad f’_s > f_s. La scelta dei simboli aggiunti viene fatta in modo che essi dipendano in modo deterministico da quelli già presenti, rendendo così la sequenza trasmessa ridondante, allo scopo di ridurre il valore della probabilità di errore. Infatti la dipendenza (nota) tra i simboli trasmessi permette al ricevitore di "accorgersi" che si è verificato un errore, dato che tale dipendenza non è più rispettata, e quindi il ricevitore può attuare delle contromisure, come quella di inviare una richiesta di ritrasmissione, oppure se la ridondanza introdotta è sufficientemente elevata, tentare di correggere errori isolati [17]   [17] Si parla in questo caso di codifica FEC, ovvero di Forward Error Correction.. Dopo aver (eventualmente) svolto le possibili contromisure, i simboli aggiunti vengono rimossi al lato ricevente da parte di un blocco di decodifica di canale.

Ha uno scopo per così dire “inverso” a quello della codifica di canale: la codifica di sorgente infatti rimuove la dipendenza (ora in senso statistico) tra i simboli presenti nella sequenza prodotta dalla sorgente, determinando la riduzione del numero di simboli da trasmettere per unità di tempo [18]   [18] Pensiamo per similitudine ad un imballaggio, il cui contenuto è prima disposto in modo da occupare il minimo volume (codifica di sorgente), ed a cui viene poi aggiunto del materiale antiurto (codifica di canale)., che passa così da f_s ad f’_s < f_s. Un tipico esempio è rappresentato dagli algoritmi di compressione per i documenti su computer, come ad es. i file zippati: in tal caso il fattore di compressione ottenibile dipende dalla natura del file, ed è tanto maggiore quanto più questo presenti caratteristiche di ripetitività, ovvero di predicibilità del suo contenuto. Pertanto l’uscita di un codificatore di sorgente è una sequenza di simboli tendenzialmente indipendenti tra loro, avendo limitato la predicibilità di un simbolo a partire dai circostanti.

Poniamoci il problema di utilizzare un canale numerico per effettuare una trasmissione analogica: il vantaggio di una tale “contorsione” è da ricercarsi nel migliore comportamento della trasmissione numerica rispetto ai disturbi, nonché alla sua generalità [19]   [19] Nei collegamenti numerici non occorre specializzare il metodo di trasmissione al mezzo a disposizione, anzi quest’ultimo è totalmente "mascherato" dal fornitore del collegamento numerico stesso, e dal modem che viene utilizzato.. Per riuscire nello scopo occorre che il segnale s(t) prodotto dalla sorgente analogica venga prima campionato prelevandone i valori s^•_n in corrispondenza degli istanti t = nT_c, ossia con una velocità di f_c = ¹⁄_Tc campioni/secondo, e quindi quantizzato approssimando i valori s^•_n mediante un insieme finito di L valori, producendo una sequenza numerica s_n di simboli appartenenti ad un alfabeto finito. Questa coppia di operazioni è indicata come conversione analogico-digitale o a/d, e la sequenza s_n può essere rappresentata da una sequenza binaria facendo corrispondere M = ⌈log₂L⌉ bit [20]   [20] La notazione M = ⌈log₂L⌉ individua l’intero superiore del valore racchiuso tra le semiparentesi ⌈⌉. Ad esempio se L = 21 allora log₂21 = 4, 3923.. e dunque M = ⌈4, 3923⌉ = 5, ovvero occorrono 5 bit/campione. ad ognuno dei simboli L − ari. Dopo le operazioni di co-decodifica e trasmissione, un dispositivo di conversione digitale-analogica (dac) posto al lato ricevente provvede a ricostruire il segnale s(t) originario. [21]   [21] L’utilizzo di dispositivi di conversione digitale-analogico è molto comune nella realtà odierna, un esempio tra tutti è quello dei CD audio, vedi https://it.wikipedia.org/wiki/CD_Audio

L’approssimazione dei campioni s^•_n mediante un insieme finito di valori introduce una distorsione, dato che il dac opera su valori approssimati e non su quelli reali. L’effetto risultante è come se presso la destinazione fosse presente un disturbo additivo e_q(t), detto rumore di quantizzazione, che si somma al segnale originario. L’entità di tale disturbo è inversamente legata alla risoluzione del quantizzatore, ovvero alla capacità di differenziare tra valori di ingresso molto vicini tra loro. In definitiva, la distorsione risulta tanto minore quanto maggiore è la velocità del flusso informativo prodotto dal quantizzatore, espresso in bit/secondo.

Se ne parla al cap. 9, e deriva da una serie di teoremi enunciati negli anni ’50 da Claude Shannon, le cui conseguenze possono essere riassunte come