6.1 Teoria delle probabilità
Tratta delle caratteristiche
regolari di fenomeni
irregolari o
casuali. Una prima
definizione di probabilità è quella fornita dalla teoria
frequentista, che la associa al limite a cui tende il rapporto tra numero di casi favorevoli rispetto al numero di casi totali: se ripetendo
N volte un esperimento la circostanza
A si verifica per
nA volte la sua frequenza relativa vale
nA ⁄ N, da cui si deriva la probabilità di
A come
PrA = limN → ∞nA N
In termini più astratti, l’insieme di tutte le circostanze possibili può essere pensato come un insieme algebrico, i cui elementi (o punti) sono appunto le diverse circostanze. I punti possono essere raggruppati in sottoinsiemi (eventualmente vuoti o di un solo punto) per i quali valgono le proprietà di unione, intersezione, complemento, inclusione...
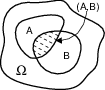
I fenomeni fisici sono posti in relazione con i punti degli insiemi suddetti mediante il concetto di
spazio campione Ω, che è l’unione di tutti i possibili risultati di un
fenomeno aleatorio, mentre i sottoinsiemi dello spazio campione sono detti
eventi. L’intero spazio è l
’evento certo, mentre l’insieme vuoto corrisponde all’evento impossibile
φ (od evento
nullo). Una
unione ∪ di eventi corrisponde all’evento che si verifica ogni qualvolta se ne verifichi
un suo componente, mentre
l’intersezione ∩ è verificata se
tutti i componenti lo sono. Ad esempio, il lancio di un dado genera uno spazio con 6 punti (eventi) disgiunti. Uno spazio campione può avere un numero di punti finito, infinito numerabile, o infinito.
6.1.1 Assiomi delle probabilità
Costituiscono le basi da cui derivano i teoremi successivi, affermando che
- 0 ≤ Pr(A) ≤ 1: la probabilità di un evento è compresa tra 0 ed 1;
- Pr(Ω) = 1: la probabilità dell’evento certo è 1;
- Se Pr(Ai ∩ Aj) = φ allora Pr( ∪ Ai) = ∑ Pr(Ai): la probabilità dell’unione di eventi disgiunti è la somma delle singole probabilità.
6.1.2 Teoremi di base
- Pr(ϕ) = 0: la probabilità dell’evento impossibile è nulla;
- Pr(A∩B) + Pr(A∩B) = Pr(A), e Pr(B) + Pr(B) = 1: un evento ed il suo complemento riempiono lo spazio (detto anche teorema delle probabilità totali);
- Pr(A∪B) = Pr(A) + Pr(B) − Pr(A∩B): la probabilità dell’evento intersezione si conta una volta sola. Esempio alla nota;
- Se B ⊆ A allora Pr(B) ≤ Pr(A): quando l’evento B è contenuto in A il verificarsi del primo implica il secondo.
6.1.3 Probabilità congiunta, condizionata e marginale
Può avvenire che il verificarsi di un evento
influenzi il verificarsi o meno di un altro. Si dice allora che lo condiziona, ovvero che l’evento influenzato è
condizionato. La probabilità che avvenga
A, noto che
B (evento
condizionante) si sia verificato, si scrive
Pr(A ⁄ B), e si legge probabilità (condizionata) di
A dato B, definita come
in cui
Pr(A, B) = Pr(A∩B) è la probabilità
congiunta che
A e
B si verifichino entrambi, ed a patto che
Pr(B) ≠ 0 (altrimenti anche
Pr(A ⁄ B) è zero!). Viceversa, le probabilità dei singoli eventi
Pr(A) e
Pr(B) sono indicate come probabilità
marginali.
Esercizio Valutare la probabilità condizionata Pr(A ⁄ B) che lanciando un dado si ottenga un numero pari (evento A = (pari)), condizionatamente all’evento B che il numero sia >2. Soluzione alla nota .
Invertendo la definizione
(10.111) la probabilità
congiunta può essere ottenuta anche come
Pr(A, B) = Pr(A ⁄ B)Pr(B); inoltre, gli eventi condizionante e condizionato si possono invertire di ruolo, permettendo di scrivere anche:
Pr(A, B) = Pr(B ⁄ A)Pr(A). Eguagliando le due ultime espressioni per la probabilità congiunta si ottiene la via per calcolare una probabilità
condizionata a partire dall’altra, qualora si conoscano entrambe le
marginali:
6.1.4 Probabilità a priori e a posteriori, teorema di Bayes
A volte un determinato evento
A non può essere osservato direttamente, ma se
A è in qualche modo legato ad un secondo evento
B, che invece possiamo osservare, la probabilità condizionata
Pr(A ⁄ B) prende il nome di probabilità
a posteriori,
poiché indica un valore di probabilità valutato
dopo la conoscenza di
B. Viceversa, in tale contesto la probabilità marginale
Pr(A) viene ora indicata come
a priori, ovvero
presunta senza aver potuto osservare nulla.
In generale si conosce solamente
Pr(A) e
Pr(B ⁄ A), mentre per calcolare
Pr(A ⁄ B) occorre conosce
Pr(B), vedi
(10.112).
Quest’ultima quantità si determina
saturando la probabilità congiunta
Pr(A, B) rispetto a tutti i possibili eventi marginali
Ai:
Pr(B) = ⎲⎳iPr(B, Ai) = ⎲⎳iPr(B ⁄ Ai)Pr(Ai)
a patto che risulti
Pr(Ai, Aj) = 0 e
∪Ai = Ω, ovvero che gli eventi
Ai siano disgiunti e che il loro insieme
{Ai} costituisca una partizione dello spazio degli eventi
Ω, come rappresentato in figura.
L’ultima relazione ci permette di enunciare il
teorema di Bayes, che mostra come ottenere le probabilità
a posteriori a partire da quelle
a priori e da quelle condizionate
in senso opposto:
Pr(Ai ⁄ Bj) = Pr(Bj ⁄ Ai)Pr(Ai) ⎲⎳kPr(Bj ⁄ Ak)Pr(Ak)
Al §
17.1.1 è mostrata l’applicazione di queste considerazioni ad un problema di decisione statistica tipico delle telecomunicazioni, relativo alla ricezione binaria. Di seguito, invece, è illustrato un esempio più diretto di applicazione del teorema di Bayes.
Un sistema di comunicazione radio è affetto da attenuazioni supplementari causate da pioggia. Indicando con FS l’evento che il sistema vada fuori servizio, e conoscendo le probabilità condizionate Pr(FS ⁄ piove) = 0.5, Pr(FS ⁄ non piove) = 0.05 e la probabilità marginale Pr(pioggia) = 0.03, determinare:
- La probabilità di fuori servizio Pr(FS), indipendentemente dal verificarsi o meno dell’evento piovoso;
- La probabilità che stia piovendo, sapendo che il sistema è fuori servizio.
Risposte alla nota ).
6.1.5 Indipendenza statistica
Si verifica quando
Pr(A ⁄ B) = Pr(A)
in quanto il verificarsi di
B non influenza
A. Come conseguenza, per due eventi statisticamente indipendenti
avviene che
- Quale è la probabilità che, lanciando 3 volte un dado, esca 3 volte 1 ? Risultato ().
- Un’urna contiene 2 biglie bianche e 3 nere. Qual è la probabilità che su 2 estrazioni consecutive senza reinserimento, escano le 2 biglie bianche ? Risultato ().
- Qual è la probabilità che 2 carte, estratte a caso da un mazzo da bridge da 52, siano K e Q ? Risultato ().