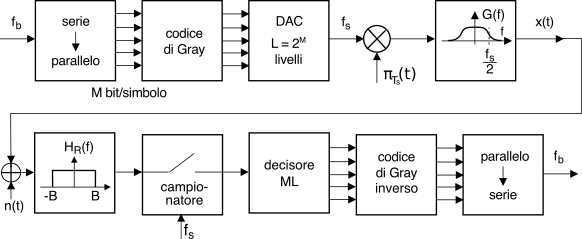
15.4 Probabilità di errore per trasmissioni di banda base
Fin qui abbiamo trascurato di prendere in considerazione gli effetti del rumore additivo, a cui si è accennato al §
15.1.1, e che provoca la ricezione di un segnale
x(t) = r(t) + n(t). Al segnale utile
r(t) risulta dunque sovrapposto un diverso segnale
n(t) indicato come disturbo o rumore (
noise ),
membro di un processo ergodico (vedi §
6.3), con densità di probabilità del primo ordine
gaussiana (vedi §
6.2.4) a media nulla, e spettro di densità di potenza
bianco, ossia costante in frequenza.
Nel caso in cui siano presenti più cause di disturbo, anche localizzate in punti diversi del collegamento, si fa in modo (vedi §
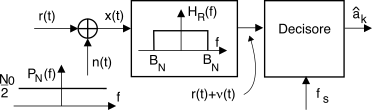
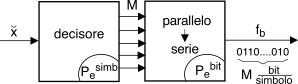
8.4) di ricondurle tutte ad un’unica fonte di rumore (equivalente) in ingresso al decisore. Come appare dalla figura a pag.
1, l’effetto del rumore è quello di causare degli
errori nelle decisioni sui livelli, e quindi sui simboli e sui bit ricevuti.
Sviluppiamo dunque una analisi per valutare la
probabilità di questi errori, in funzione delle grandezze che vi contribuiscono, in modo a poter successivamente affrontare problematiche di progetto, vedi §
19.1.
15.4.1 Banda di ricezione e dinamica del rumore
Come anticipato il disturbo
n(t) è la realizzazione di un processo ergodico gaussiano a valor medio nullo e con spettro di densità di potenza
bianco o costante
PN(f) = N0 ⁄ 2
spesso indicato come
Additive White Gaussian Noise o AWGN
.
Allo scopo di limitare la potenza del rumore alla minima possibile il ricevitore vero e proprio è preceduto da un filtro passa-basso ideale con risposta in frequenza
HR(f) limitata in una banda
± BN (detta
banda di rumore, vedi §
14.1.2), in modo da lasciar passare
per intero le componenti frequenziali del segnale
r(t) e limitare la banda del rumore
ν(t) in uscita da
HR(f) al minimo. Il rumore
filtrato ν(t) è anch’esso un processo gaussiano ergodico (vedi nota
383 a pag.
1) a media nulla, la cui potenza
vale
Pν = ∞⌠⌡ −∞PN(f)|HR(f)|2df = BN⌠⌡ − BNN02 df = N0BN
In virtù della ergodicità di
ν(t) il valore di
Pν
eguaglia quello del momento di secondo ordine
m(2)ν = E{(ν)2} di una v.a.
ν ottenuta campionando una sua qualsiasi realizzazione; dato inoltre che
n(t) e dunque
ν sono a media nulla, si ha
m(2)ν = σ2ν e quindi
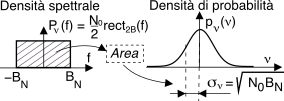
Pν individua anche
la dinamica dei valori della v.a. di rumore sovrapposta ai valori di segnale, come esemplificato in figura.
15.4.2 Dinamica del segnale e decisione a massima verosimiglianza
Proseguiamo l’analisi descrivendo il segnale ricevuto nella forma
con
g(t) che è un impulso di Nyquist
(21.3); si assume inoltre una perfetta sincronizzazione temporale (§
15.7) in modo da poter considerare l’ISI assente. Gli elementi della sequenza
{a[k]} sono v.a. discrete, i.i.d. con d.d.p. uniforme, che assumono uno tra
L possibili valori
ai equispaziati in un intervallo con dinamica
Δ = aL − a1, in modo da poter scrivere
ai = a1 + ΔL − 1 ⋅ (i − 1) con
i = 1, 2, .., L.
Agli istanti
t = kTs = k ⁄ fs multipli del periodo di simbolo
Ts il decisore acquisisce il valore di segnale più rumore
x(kTs) = (r(t) + ν(t))|t = kTs ed anziché ritrovare il valore
a[k] = ai(k) del simbolo trasmesso, osserva la realizzazione di una v.a. gaussiana
x̆ = x(kTs) con valor medio
ai(k) e varianza
σ2ν = N0BN, essendo
ν(t) a media nulla. Per stabilire quale valore
ai sia stato (più probabilmente) associato al simbolo
k − esimo il ricevitore effettua quindi una decisione
di massima verosimiglianza (o
ml, vedi §
6.6.2.1) confrontando tra loro le densità di probabilità
condizionate alle diverse ipotesi che sia stato trasmesso uno tra i simboli
ai:
e scegliendo per l’
^ai tale che
PX ⁄ ^ai(x̆) è la più grande, ossia
^ai = argmaxai{PX ⁄ ai(x̆)}
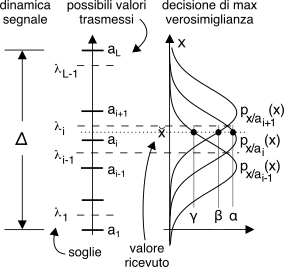
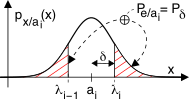
Il criterio di massima verosimiglianza equivale pertanto (vedi figura) a definire
L − 1 soglie di decisione
λi,
i = 1, 2, .., L − 1 poste
a metà tra i valori
ai ed
ai + 1, e decidere per il valore
ai se il segnale ricevuto
x̆ cade all’interno dell’intervallo compreso tra
λi − 1 e
λi (), dato che (con riferimento alla notazione in figura) ciò corrisponde ad imporre
α = PX ⁄ ai(x̆) > β = PX ⁄ ai + 1(x̆) > γ = PX ⁄ ai − 1(x̆)
15.4.3 Probabilità dell’errore gaussiano
A seguito dell’applicazione del criterio di massima verosimiglianza il decisore commette errore quando, a fronte della trasmissione di un simbolo
ai, il campione di rumore filtrato
ν(kTs) assume un valore abbastanza elevato da far oltrepassare a
x̆ una soglia di decisione, ovvero qualora
|ν(kTs)| > δ in cui
δ è la metà dell’intervallo tra due soglie e cioè
δ = |λi − ai| = Δ2(L − 1). La probabilità di questo errore si dice
condizionata alla trasmissione di
ai e vale
che chiameremo
Pδ,
e che rappresenta (vedi figura) la somma delle aree tratteggiate.
Lo stesso valore
Pδ è valido per tutti gli indici
i compresi tra
2 ed
L − 1, mentre per
a1 ed
aL la probabilità di errore è dimezzata, in quanto in tali casi esiste solamente una delle due soglie il cui superamento determina una decisione errata, e dunque scriviamo
Pe ⁄ a1 = Pe ⁄ aL = 12 Pδ. Applicando ora alla
(21.9) il cambiamento di variabile descritto al §
6.2.4, si ottiene
Pδ = erfc⎧⎩λi − ai√2σν⎫⎭, ed esprimendo l’intervallo
λi − ai in funzione della dinamica di segnale
Δ troviamo
Per arrivare all’espressione della probabilità di errore
incondizionata, ovvero indipendente dall’identità del simbolo trasmesso, occorre eseguire una operazione di
valore atteso (§
6.2.2) rispetto a tutti gli indici
i, con
i = 1, 2, ..., L, cioè pesare le diverse probabilità di errore condizionate
Pe ⁄ a1 con le rispettive probabilità
Pi = Pr{ai} degli eventi condizionanti
ai. Avendo assunto l’ipotesi di valori
ai equiprobabili risulta
Pi = 1L e quindi
in cui si è tenuto conto del diverso valore della probabilità condizionata per i livelli intermedi e per i due agli estremi.
15.4.4 Parametri di sistema e di trasmissione
Il risultato ottenuto, benché già idoneo a valutare la
Pe con i dati con cui è stata impostata l’analisi, deve attraversare qualche ulteriore passaggio per poter esprimere
Pe in funzione dei parametri di sistema potenza
di segnale PR, densità di potenza di
rumore Pν(f) = N0⁄2 e
velocità binaria fb, nonché dei parametri
di trasmissione L e
γ, in modo da poter affrontare gli aspetti di
bilancio di collegamento (cap.
19). Approfondiamo a tale scopo alcune relazioni per giungere alla definizione di un nuovo parametro riassuntivo.
Legame tra potenza del segnale
PR e dinamica
Δ
Al §
15.8.1 si ottiene che, sotto le ipotesi (che manterremo valide anche nel seguito) in cui
- si adotti un impulso di Nyquist a coseno rialzato con roll-off γ;
- i valori dei simboli a[k] siano statisticamente indipendenti, equiprobabili, a media nulla e distribuiti uniformemente su L livelli con dinamica aL − a1 = Δ;
la relazione tra
PR e
Δ risulta
Essendo il termine
L + 1L − 1⎛⎝1 − γ4⎞⎠ decrescente per
L ≥ 2 e
γ ≥ 0, la potenza ricevuta assume il valore massimo
PR = Δ24 nel caso di trasmissione binaria a banda minima, ossia per
L = 2 e
γ = 0. Per essere utilizzata nella
(21.10), la
(21.12) deve prima essere invertita in modo da esprimere
△ in funzione di
PR
Facciamo ora entrare in gioco anche la conoscenza di
fb, introducendo un nuova grandezza:
Dato che la potenza rappresenta l’energia sviluppata per unità di tempo, e che in un secondo
entrano fb bit, possiamo pensare
PR suddivisa tra i bit presenti, in modo da definire una quantità detta
energia per bit
che riassume in sé i parametri di sistema
potenza di segnale e
velocità binaria, mentre non dipende dai
parametri di trasmissione L e
γ, e consente di sostituire
PR = Ebfb nella
(21.13).
Dipendenza di
Pν da
L e
γ
Ora nella
(21.10) l’unico termine rimasto incognito sembra essere
σν, pari a
Pν per via del valor medio nullo del rumore. D’altra parte la potenza di rumore
Pν = N0BN dipende anche da
L e
γ attraverso la
(21.5) ovvero
BN = fb(1 + γ)2log2L, ma vorremmo mantenere separati i contributi dei parametri
di sistema da quelli
di trasmissione. Allora, anziché tentare di esprimere la
(21.10) in funzione di
SNR = PRPν , introduciamo un diverso
rapporto di qualità. Definizione di Eb/No
e suo contributo all’SNR
Esprimendo le potenze
Pν e
PR in funzione di
Tb = 1 ⁄ fb, e considerando sempre un segnale dati a coseno rialzato, le eq.
(21.5) e
(21.14) permettono di scrivere
in modo da ottenere
Quindi, mentre
SNR dipende anche da
L e da
γ, il rapporto
EbN0 coinvolge solo i parametri di sistema
PR,
fb ed
N0: sarà questa la variabile
indipendente rispetto alla quale valutare la
Pe.
15.4.5 Probabilità di errore per simbolo
Non resta ora che inserire la (
21.13) nella espressione di
Pδ (eq.
21.10), ricordare che
σ2ν = Pν, e tenere conto della (
21.16), in modo da ottenere la probabilità di decidere per un simbolo
aj diverso da quello trasmesso
:
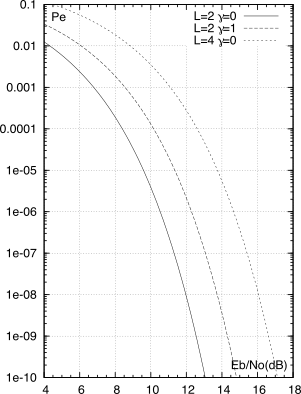
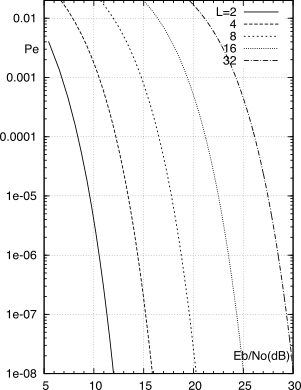
la cui dipendenza da
EbN0 (espresso in dB, vedi §
8.1) è graficata alla Fig
15.31 per tre condizioni operative.
In particolare notiamo che per
L = 2 e
γ = 0 la
(21.17) diviene
mentre, a parità di
Eb⁄N0, scelte progettuali diverse da
L = 2 e
γ = 0 determinano immancabilmente un peggioramento della
Pe: tali scelte possono essere comunque adottate per soddisfare esigenze di risparmio di banda (aumentando
L), e per ridurre i termini di interferenza intersimbolica (aumentando
γ).
Due domande riassuntive:
- perché Pe peggiora se aumento i livelli? Risposta ().
- perché Pe peggiora se aumento γ? Risposta ().
15.4.6 Relazione con il filtro adattato
Qualche lettore può chiedersi come mai si sia utilizzato come filtro di ricezione un semplice passa basso, anziché operare come descritto al §
7.6. Tale opzione viene esplorata al §
15.5, ma possiamo notare fin da subito l’equivalenza tra i risultati
(21.18) e
(10.176). Infatti l’energia di un singolo impulso
Eg equivale all’energia per bit
Eb, ed un segnale dati a media nulla e simboli binari corrisponde ad una segnalazione antipodale. Quanto all’adozione di un impulso di Nyquist a coseno rialzato con
γ = 0, ovvero a
banda minima (§
15.2.2.3), ciò corrisponde ad aver posto
G(f) = Ts rectfs(f), ovvero proprio il passa basso ideale qui adottato in ricezione, che si rivela essere anche
adattato nel caso appunto di trasmissione binaria a banda minima. Viceversa, il passa basso ideale non è più adattato qualora si scelga
g(t) con
γ > 0, e questo è il motivo della dipendenza della
(21.17) dal parametro
γ.
15.4.7 Compromesso banda - potenza
Osservando le fig.
15.31 e
15.39 notiamo che al crescere di
L, e dunque occupando una banda minore, si può ottenere la stessa
Pe solo a patto di aumentare
Eb⁄N0, ovvero (a parità di
fb) aumentando la potenza trasmessa: questo è un aspetto di un risultato più generale della
teoria dell’informazione. Si può infatti dimostrare (vedi pag.
1) che
è possibile trasmettere senza errori (ricorrendo a tecniche di codifica di canale ottimali) purché la velocità di trasmissione
fb non ecceda la
capacità di canale, definita come
in cui
B è la banda del canale,
PR la potenza ricevuta, e
N0B la potenza del rumore. Un secondo canale con minor
banda passante B dispone di una minore capacità, in quanto anche se in tal caso l’argomento di
log2(.) aumenta, il logaritmo cresce più lentamente di quanto non decresca
B che compare a fattore nella
(21.19); pertanto per mantenere la stessa capacità è necessario trasmettere con una maggiore potenza di segnale
PR. Per questo motivo qualora sussistano limitazioni di potenza ma non di banda, come ad esempio nelle
comunicazioni satellitari, conviene occupare la maggior banda possibile, mantenendo
L = 2, in modo da risparmiare potenza. L’argomento viene approfondito a pag.
1.
Coerentemente con queste osservazioni, un ulteriore aumento di banda occupata si può ottenere con l’aggiunta di bit di ridondanza, come avviene applicando le tecniche di
codifica di canale introdotte al §
15.6 ed approfondite cap.
17, dato che a questo corrisponde un
aumento della velocità di trasmissione complessiva. Mostreremo in tale sede come ciò consenta di
ridurre la probabilità di errore, e dunque migliorare la
fedeltà del flusso binario, anche a parità di potenza ricevuta.
15.4.8 Diagramma ad occhio in presenza di rumore
Si tratta dello stesso tipo di grafico già descritto a pag.
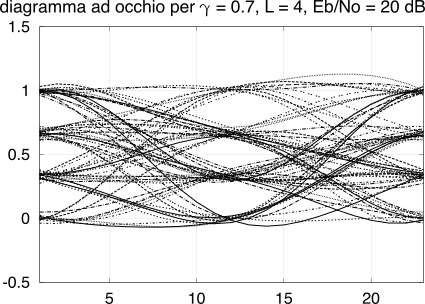
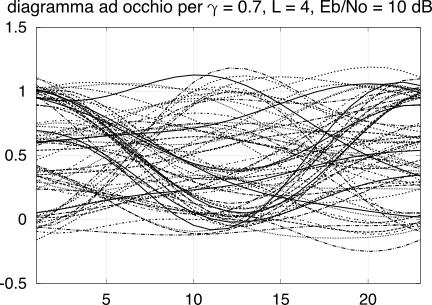
1, e che ora ci aiuta a valutare in modo visivo la qualità di una trasmissione numerica. In fig.
15.32 sono riportati i grafici per un segnale dati a 4 livelli, in presenza di due diversi valori per la potenza di rumore: notiamo che al peggiorare del rapporto
EbN0 da 20 a 10 dB la zona priva di traiettorie (
l’occhio) riduce la sua estensione verticale (
tende a chiudersi). Con un tale approccio la qualità di un segnale numerico può essere valutata in modo approssimato, qualora si disponga di un oscilloscopio, esaminando il
grado di apertura dell’occhio.
15.4.9 Valutazione della probabilità di errore per bit
La probabilità di errore
Psimbe (21.17) si riferisce all’evento di decidere per la ricezione del
simbolo ai quando invece ne è stato trasmesso un altro, mentre ora intendiamo valutare la probabilità che sia errato
un qualunque bit presente nel flusso a velocità
fb,
ricostruito dopo la
serializzazione (vedi figura a lato) della codifica binaria associata al simbolo
ai emesso dal decisore.
Precisiamo subito che quando la decisione per ai è errata significa che in realtà è stato trasmesso ai − 1 o ai + 1 e non un altro simbolo qualsiasi, dato che la probabilità che il rumore provochi il salto di due o più livelli è molto inferiore a quella di un salto singolo. Questa circostanza ha permesso di ideare il procedimento (che ora illustriamo) di associare ad ogni simbolo (o livello) una particolare codifica binaria, capace di garantire la presenza di un solo bit errato per ogni simbolo errato.
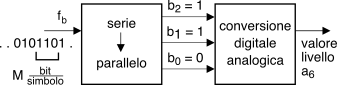
Per illustrare il problema di cui questo codice è soluzione, riprendiamo in esame la fig.
15.9-a) dove si mostra un segnale dati multilivello con
L = 4 per il quale i valori
ai sono associati a coppie di bit
b1b0 che sono la semplice
codifica binaria dell’indice
i corrispondente, ovvero
i = b121 + b020: ciò significa che i valori
ai possono essere prodotti da un semplice convertitore D/A (pag.
1)
alimentato da una parola di
M bit
bM − 1…b1b0 per una trasmissione ad
L = 2M livelli, come mostrato a lato per
M = 3.
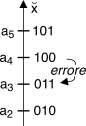
Prendiamo quindi in esame la situazione (per
M = 3) mostrata a lato, e consideriamo ad esempio di trasmettere il livello
a4 a cui è associata la codifica
100, e che il decisore a causa del rumore commetta l’errore di ritenere di aver ricevuto il livello
a3, associato alla sequenza
011: in tal caso avremmo sbagliato tutti e tre i bit!
Per evitare di osservare un numero di bit errati che dipende dal simbolo trasmesso e dal segno del rumore, la conversione D/A viene fatta precedere
da una
riscrittura della parola di
M bit attuata consultando una tabella dove è memorizzato il
codice di Gray.
Possiamo immaginare l’operazione come quella di un accesso a una
memoria associativa, in cui la parola originaria costituisce
la chiave con cui individuare la parola
codificata da utilizzare al suo posto, come rappresentato nella tabella a lato per
M = 3. Notiamo che la colonna di sinistra ha la proprietà di codificare righe adiacenti mediante configurazioni binarie che differiscono tra loro
in una sola posizione, ovvero per un solo bit. Per analizzare la conseguenza di ciò, osserviamo che ora al posto della parola
110 di ingresso (quarta riga) si usa il codice
100 a cui il DAC fa carrispondere il livello
a4, lo stesso dell’esempio precedente.
In ricezione si attua la trasformazione inversa che utilizza la tabella
al contrario, individuando nella seconda colonna la riga in cui compare la
codifica binaria associata al livello ricevuto, e sostituendo ad essa la parola nella prima colonna. In assenza di errori si riottiene la parola binaria originale; se invece si verifica un errore, ovvero ad es. come prima al posto di
a4 si decide per
a3 (
011), il
decodificatore di Gray al lato ricevente individua tale
chiave alla
5a riga della seconda colonna, a cui fa corrispondere la sequenza
010 che trova alla prima colonna, e che infatti differisce dall’originale (
110) per un solo bit (il primo).
In presenza di un errore sul simbolo il procedimento illustrato produce
sempre un solo bit errato. Ciò comporta che con
M bit a simbolo la probabilità di osservare un bit errato si riduce di
M volte rispetto a quella di errore sul simbolo, ossia risulta
Pbite = Psimbe ⁄ M, dato che
Esempio Con L = 256 livelli ovvero M = 8 bit/simbolo la Pe sul bit si riduce di log2L = 8 volte.
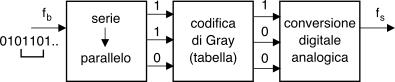
Riassumendo La figura
15.38 mostra l’intera sequenza di operazioni necessarie a generare un segnale dati multilivello, con codifica di Gray ed impulso a coseno rialzato, e quindi riceverlo recuperando la sequenza trasmessa. Ricordiamo che mentre al flusso binario di ingresso compete una velocità di
fb bit/secondo, la sequenza multilivello possiede invece un ritmo di
fs = fbM = fblog2L simboli/secondo, ed il segnale dati risultante
x(t) occupa una banda a frequenze positive
B = fs(1 + γ)2 = fb(1 + γ)2log2L, vedi eq.
(21.5).
15.4.9.2 Probabilità di errore per bit
Alla luce dell’evidente vantaggio di ottenere un solo bit errato per ogni simbolo errato il codice di Gray discusso al § precedente viene adottato in modo
sistematico, e la
(21.20) può essere letta “l’evento di errore
sul bit si verifica quando il simbolo a cui appartiene è errato,
e il bit è quello errato, ovvero
Pr{bit errato} = Pr{simbolo errato} ⋅ Pr{bit errato/simbolo errato} = Psimbe ⋅ 1log2L” . L’espressione
(21.17) della
Pe per bit nel caso si adotti una codifica di Gray diviene quindi
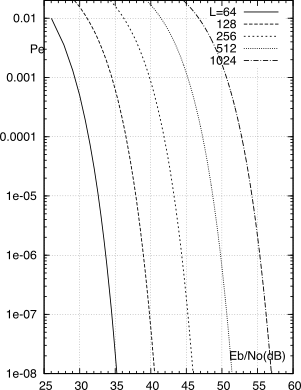
Le curve in fig.
15.39 mostrano il valore di
Pbite così determinato, per
γ = 0, in funzione di
EbN0 espresso in dB, per diversi valori di
L.
Valori di
γ ≠ 0 equivalgono ad un peggioramento per
EbN0|dB pari a
10 log10 (1 + γ)⎛⎝1 − γ4⎞⎠, o detto in altri termini, conseguono la stessa
Pbite del caso
γ = 0, a patto di incrementare
EbN0|dB della stessa quantità.
Dimensionamento di una trasmissione numerica
Una tipica metodologia operativa di progetto può basarsi sull’imporre un determinato valore di Pbite, una volta nota la banda disponibile B e la velocità fb richiesta. In tal caso
- in base a B e fb si può determinare il valore di L mediante la (21.5), nell’ipotesi di adottare γ = 0;
- in base alle curve di fig. 15.39 ed al valore di L individuato, si determinano i valori di Eb⁄N0 (in dB) necessari per ottenere la Pbite;
- noto il livello di rumore N0, si determina Eb;
- note le esigenze di precisione nella temporizzazione, si impone un valore del roll-off γ, e conseguentemente si aumenta il valore di Eb;
- si determina la minima potenza che è necessario ricevere, come WRmin = Eb ⋅ fb.
Esempio Un canale analogico con banda a frequenze positive B = 500 KHz è utilizzato per realizzare la trasmissione numerica di un flusso binario a velocità fb = 10 Mbps adottando una codifica di linea multilivello con codice di Gray ed impulso a banda minima. Al punto di ricezione è presente un rumore gaussiano bianco a media nulla e densità di potenza Pn(f) = 10 − 12 WHz, la cui potenza è limitata dal ricevitore mediante un filtro passa basso con la medesima banda del canale. Desiderando una Pe ≤ 10 − 5, determinare la potenza di segnale che è necessario ricevere.
Svolgimento Per prima cosa determiniamo il numero di livelli: sapendo che
B = fb2 1log2L si ottiene
log2L = fb2B = 0.5 ⋅ 10715 ⋅ 105 = 10, e dunque
L = 210 = 1024 livelli. Dalle curve
Pe(Eb⁄N0) otteniamo quindi che per avere
Pe = 10 − 5 con
1024 livelli occorre un
Eb ⁄ N0|dB ≥ 54 dB, ossia
Eb ⁄ N0 ≥ 105.4. Osservando infine che
N0 = 2 Pn(f) si ottiene la potenza del segnale come
Px = Eb ⋅ fb = EbN0 ⋅ N0 ⋅ fb = 105.4 ⋅ 2 ⋅10 − 12 ⋅ 10 ⋅106 = 2 ⋅ 100.4 = 5.2 Watt.
A pag.
1 viene proposto un diverso esercizio che comprende anche alcuni concetti introdotti alla sezione
15.6.