9.4 Misure di informazione per una coppia di v.a.
Descrivono da un punto di vista informativo i messaggi prodotti da una coppia di sorgenti, ovvero componenti di una v.a. bidimensionale; i risultati ottenuti saranno utilizzati nel contesto della quantizzazione (§
9.5) e della codifica di canale (cap.
17). Vengono poi introdotti altri due risultati (§§
9.4.4 e
9.4.5), utilizzati specificatamente in altri contesti. Per semplicità, le definizioni vengono espresse nei termini di v.a. discrete.
9.4.1 Entropia congiunta
Si riferisce a due v.a. X e
Y le cui realizzazioni sono descritte dalle d.d.p. marginali
p(x) e
p(y) e dalla d.d.p. congiunta
p(x, y), ed è definita come
H(X, Y) = H(Y, X) = − ⎲⎳x⎲⎳y p(x, y) log2 p(x, y)
L’entropia congiunta risulta sempre non negativa, e delimitata tra
0 ≤ max{H(X), H(Y)} ≤ H(X, Y) ≤ H(X) + H(Y)
con l’ultimo
≤ che diviene un’uguaglianza qualora le v.a. siano statisticamente indipendenti ovvero
p(x, y) = p(x)p(y). Nel caso di v.a. continua sussiste l’equivalente definizione per l’entropia differenziale congiunta
9.4.2 Entropia condizionale
Come la precedente si riferisce a due v.a. X e
Y descritte dalle d.d.p.
p(x),
p(y) e dalla d.d.p. condizionata
p(y ⁄ x) = p(x, y)⁄p(x), viene definita come
e per essa sussiste la relazione
che si ottiene dalla
(10.238) considerando che
p(y ⁄ x) = p(x, y)⁄p(x). In base alla relazione analoga per
p(x ⁄ y) è altrettanto vero che
H(X ⁄ Y) = H(X, Y) − H(Y), e dunque sussiste anche
l’equivalente del teorema di Bayes (§
6.1.4), ovvero
H(Y ⁄ X) = H(X ⁄ Y) + H(Y) − H(X).
La
(10.239) può essere
interpretata considerando che mentre
H(X, Y) esprime il numero medio di bit di informazione associati alla conoscenza di una coppia di realizzazioni
(x, y), l’osservazione della sola v.a.
X apporta una informazione media di
H(X) bit/simbolo. Pertanto sono necessari solamente
H(X, Y) − H(X) ulteriori bit (in media) per descrivere anche la conoscenza di
Y, una volta che
X sia nota. Per la
(10.238) risulta
0 ≤ H(Y ⁄ X) ≤ H(Y)
in cui la prima relazione è una uguaglianza se (e solo se)
p(y ⁄ x) è una funzione deterministica e non una d.d.p., mentre
H(Y ⁄ X) = H(Y) se (e solo se)
p(y, x) = p(x)p(y) e quindi
p(y ⁄ x) = p(y).
Nel caso di v.a. continue la definizione di entropia differenziale condizionale è
h(Y ⁄ X) = − ⌠⌡x⌠⌡y p(x, y) log2p(y ⁄ x) dxdy = − ⌠⌡x p(x) ⌠⌡y p(y ⁄ x) log2p(y ⁄ x) dydx
i cui valori possono però risultare anche negativi o indeterminati (pag.
1).
9.4.3 Informazione mutua media
Anche questa grandezza tiene conto di due v.a.
X e
Y descritte dalle d.d.p. marginali
p(x) e
p(y), nonché dalla d.d.p. congiunta
p(x, y); la sua definizione è
ed ha un valore positivo o nullo, quest’ultimo se (e solo se) la v.a. sono indipendenti, ovvero
p(x, y) = p(x)p(y). Il valore di
I(X, Y) misura l’informazione che
X e
Y condividono, ovvero quanto la conoscenza di una riduce l’incertezza a riguardo dell’altra. Per essa sussistono le eguaglianze
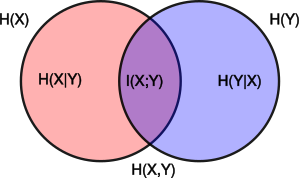
I(X;Y) = H(X) − H(X ⁄ Y) = H(Y) − H(Y ⁄ X) = H(X) + H(Y) − H(X, Y) = = H(X, Y) − H(X ⁄ Y) − H(Y ⁄ X)
che possono essere meglio apprezzate nei termini di unione, differenza ed intersezione di insiemi, come raffigurato nel diagramma mostrato a lato. In particolare, in base alle prime due eguaglianze possiamo dire che
I(X;Y) è pari all’entropia di una delle due v.a., meno il numero di bit a simbolo necessari a descriverla qualora l’altra v.a. sia nota, ovvero meno l
’incertezza residua qualora una delle due sia nota.
Anche questo concetto si applica al caso di v.a. continue, ottenendo l’espressione dell’informazione mutua media
differenziale
I(X;Y) = ⌠⌡x ⌠⌡y p(x, y) log2 p(x, y)p(x)p(y) dxdy
che
non dipende dalla dinamica delle v.a.
X e
Y come invece accadeva per l’entropia differenziale di una
(10.234) o due
(10.237) v.a.
9.4.4 Entropia relativa
Meglio nota come
Divergenza di Kullback Leibler, è una misura di quanto una d.d.p.
p(x) è differente da una seconda
q(x), di riferimento. E’ definita dall’espressione
ed è descritta anche come entropia relativa
da q a p, o divergenza
di p da q. Il suo valore è positivo o nullo, e si azzera quando
p(x) = q(x); non può essere però adottata come una
distanza, in quanto non è simmetrica (ovvero
DKL(p||q) ≠ DKL(q||p)) e non verifica la disuguaglianza triangolare.
In genere p(x) deriva da osservazioni sperimentali, mentre q(x) ne rappresenta un modello teorico, ed il valore di DKL(p||q) può essere interpretato come il numero medio di bit in più necessario a codificare i simboli x adottando un codice ottimizzato rispetto a q(x), anziché uno ottimizzato per p(x). In questo senso, DKL(p||q) misura il guadagno di informazione conseguito nel rivedere le proprie convinzioni a riguardo del fenomeno aleatorio espresso dalla v.a. X, da una d.d.p. a priori q(x), in favore della evidenza basata sui dati p(x).
Nel caso di v.a. continue la definizione
(10.241) si modifica in
DKL(p||q) = ⌠⌡x p(x) log2 p(x)q(x) dx
e, come per
I(X;Y), il suo valore non dipende dalla dinamica delle v.a.
Relazione con l’informazione mutua media
La
(10.241) può essere vista come il valore di informazione mutua media
(10.240) tra due v.a.
X e
Y, calcolato come divergenza
DKL(p(x, y)|| p(x)p(y)) della d.d.p. congiunta
p(x, y) dal prodotto
p(x)p(y) delle rispettive marginali. Dato però che la
(10.240) prevede una doppia sommatoria mentre la
(10.241) soltanto una, si preferisce scrivere
I(X;Y) = ⎲⎳x⎲⎳y p(x, y)log2p(x, y)p(x)p(y) = ⎲⎳x⎲⎳y p(x ⁄ y)p(y)log2p(x ⁄ y)p(y) p(x)p(y) = = ⎲⎳y p(y)⎲⎳x p(x ⁄ y)log2p(x ⁄ y)p(x) = EY{DKL(p(x ⁄ y)|| p(x))}
in cui la somma su
x valuta la divergenza della d.d.p. condizionata
p(x ⁄ y) dal modello
p(x), mentre la somma esterna su
y esegue il valore atteso rispetto ai valori
y. Più
p(x ⁄ y) e
p(x) sono differenti (o divergenti), e maggiore è il guadagno di informazione.
9.4.5 Entropia di Rényi
Definita in tempi più recenti, estende il concetto di entropia introdotto da Shannon
(10.217), che ne diviene un caso particolare. L’entropia di Rényi di ordine
α, con
α ≥ 0 ed
α ≠ 1, di una v.a. discreta
X con alfabeto di
n elementi
xi, di probabilità
pi, è definita come
Hα(X) = 11 − α log2 (⎲⎳ ni = 1 pαi)
In caso di v.a. uniforme con
pi = 1⁄n ∀i si ha
Hα(X) = log2n per
∀α; in generale,
Hα(X) è una funzione non crescente di
α. Per diversi specifici valori di
α accade che
- per α → 0 si ha H0(X) → log2n per qualunque d.d.p.;
- per α → 1 il valore H1(X) eguaglia quello dell’entropia classica ∑ni = 1 pi log2 1pi;
- per α → ∞ il valore Hα(X) è sempre più legato ai soli eventi più probabili.
Viene inoltre definita una
divergenza di Rényi tra due d.d.p. discrete
pi e
qi di uguale cardinalità
n come
Dα(p|| q) = 1α − 1 log2 ⎛⎝∑ni = 1 pαiqα− 1i⎞ ⎠ che, per
α → 1, corrisponde alla divergenza di Kullback-Leibler (§
9.4.4).