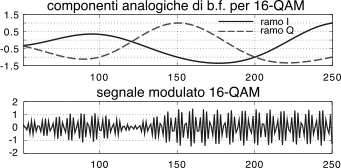Sezione 16.2: Modulazione di fase Su Capitolo 16: Modulazione numerica Sezione 16.4: Codifica differenziale 

16.3 Modulazione QAM

Questo acronimo sta per Quadrature Amplitude Modulation, ed individua la tecnica di modulazione che utilizza due portanti in quadratura come il psk
xQAM(t) = xc(t) cosω0t − xs(t) sinω0t
ma a differenza del psk, ora le componenti di banda base xc ed xs non dipendono da una stessa sequenza di fasi, ma sono originate da due flussi di dati distinti.
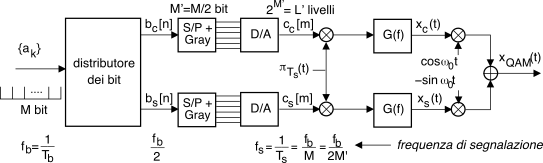
Con riferimento alla fig. 16.17, osserviamo che sebbene xc(t) e xs(t) si ottengano a partire da una medesima sequenza numerica {ak}, i bit di quest’ultima sono distribuiti alternativamente sui due rami (sequenze bc[n] e bs[n] in figura) a velocità dimezzata [837]   [837] In pratica, l’indice n si incrementa ogni due incrementi dell’indice k., suddividendo un gruppo di M bit in due simboli costituiti da M’ = M⁄2 bit.
figure f10.14.png
Figure 16.17 Architettura di un modulatore QAM
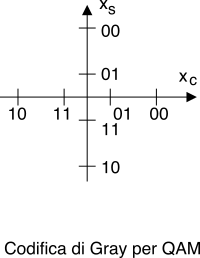
Dalle sequenze bc e bs ad M’ bit/simbolo poi si ottengono (mediante codifica di Gray) i valori cc e cs con L’ = 2M’ = 2M⁄2 = √2M = √L livelli, che attraversando in forma impulsiva il filtro G(f), danno luogo ai segnali di banda base xc ed xs.
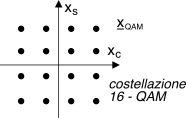
La sequenza di operazioni descritte determina una costellazione quadrata, composta da L = (L’)2 punti [838]   [838] Per come si è impostata la distribuzione dei bit tra i rami L deve risultare un quadrato perfetto. Sebbene sia possibile realizzare anche costellazioni di forma non quadrata, vedi ad es. AA.VV., A Survey on Design and Performance of Higher-Order QAM Constellations presso https://arxiv.org/pdf/2004.14708.pdf, la soluzione quadrata è preferita per semplicità realizzativa., che rappresentano le coordinate
figure f10.15.png
(nel piano dell’inviluppo complesso) in cui x è forzato a transitare in corrispondenza degli istanti di Nyquist multipli del periodo di simbolo Ts, che risulta essere pari a
Ts = Tb ⋅ M = 1fb log2L
Esempio il 16-qam si ottiene con m = 4 bit/simbolo (L = 16 = 2M = 24) e sui due rami sono presenti L’ = √16 = 4 livelli, ottenendo il risultato di una costellazione quadrata di L = 4x4 = 16 punti.
Occupazione di banda
Se G(f) è a coseno rialzato con roll off γ, allora la banda a frequenze positive di xc ed xs risulta pari a fs2 (1 + γ) = fb2log2L (1 + γ), mentre quella di xQAM è pari al doppio, a causa della modulazione am-bld-ps operata sui due rami del modulatore, ovvero
BQAM = fblog2L (1 + γ) = fs (1 + γ)
e quindi uguale a quella di ask e psk con uguale numero di livelli (di cui condivide quindi anche l’efficienza spettrale).
Dinamica delle ampiezze
Nella parte superiore della figura a lato
figure f10.86b.png
è mostrato l’andamento di xc ed xs per 5 simboli di un 16-qam realizzato a partire da un segnale dati con γ = 0.5, e si può notare che in corrispondenza di ogni periodo di simbolo entrambe assumono uno tra i valori  − 1, − 0.33,  0.33,  1. Nella parte inferiore è riportato il corrispondente segnale modulato, che come si vede non è affatto ad ampiezza costante.

16.3.1 Prestazioni di QAM

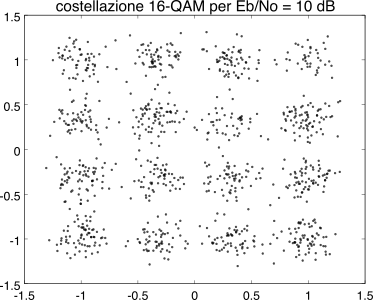
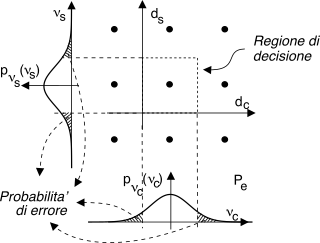
Nella parte sinistra di fig. 16.20 è mostrata la costellazione per un 16-qam in presenza di rumore (Eb⁄N0 = 10 dB). La distanza tra due punti di costellazione è maggiore (a parità di L) del caso psk, e pertanto c’è da aspettarsi un miglioramento delle prestazioni (a parità di Eb ⁄ N0), in quanto l’area che individua la probabilità di errore è ridotta.
figure f10.15a.png
figure f10.16.png
Figure 16.20 Costellazione 16-qam in presenza di rumore (a sn), calcolo della Pe sui rami (a ds)
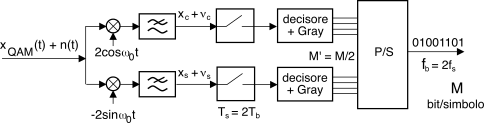
Il segnale qam viene demodulato secondo lo schema di fig. 16.21, che ci permette di constatare come su ciascuno dei due rami in fase e quadratura transita un segnale ask multilivello con L’ = √L,
figure f10.16b.png
Figure 16.21 Demodulatore qam
e dunque possiamo adottare [839]   [839] Per applicare la (21.39) dobbiamo verificare se il valore di Eb⁄N0 è lo stesso nei due casi (vedi nota 832). Mentre per N0 non vi sono dubbi, notiamo (vedi § 12.4.5 per il caso di c.a. di b.f. incorrelate) che la potenza ricevuta Px si dimezza su entrambi i rami, così come la fb, e pertanto si ottiene E’b = Px⁄2fb⁄2 =  Pxfb = Eb. l’espressione (21.39) (relativa ad un impulso g(t) a banda minima) per definire la probabilità di errore su ciascuno dei due rami, pari a
Pα  =  Pce(simbolo) = Pse(simbolo) = ⎛⎝1 − 1L’⎞⎠ erfc⎧⎨⎩√3 EbN0 log2 L’(L’)2 − 1⎫⎬⎭
Ricordando ora che L’ = √L = (L)1 ⁄ 2, e dunque log2 L’ = 12 log2 L, si ottiene
(21.46)
Pα = ⎛⎝1 − 1√L⎞⎠ erfc⎧⎨⎩√32 EbN0 log2 LL − 1⎫⎬⎭
La probabilità di errore (a simbolo) complessiva, cioè la probabilità che il segnale ricevuto d = x + ν cada fuori della regione di decisione relativa all’x trasmesso (vedi parte destra di fig. 16.20), risulta Pe(simbolo) ≃ Pα + Pα = 2Pα, assumendo trascurabile la probabilità di sbagliare entrambe xc ed xs. Questa stessa ipotesi, assieme all’utilizzo di un codice di Gray per codificare i gruppi di bit associati ai livelli dei due rami, consente di esprimere la probabilità di errore per bit come
(21.47)
PQAMe(bit)  =  Pe(simbolo)log2L = 2log2 L ⎛⎝1 − 1√L⎞⎠ erfc⎧⎨⎩√32 EbN0 log2 LL − 1⎫⎬⎭
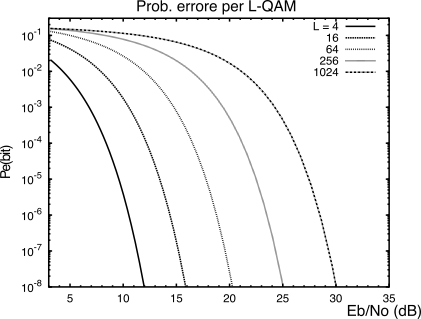
In figura 16.22 troviamo le curve dei valori di Pe(bit), per diversi valori di L, al variare di EbN0 espresso in dB; il confronto con le curve relative al psk permette di valutare l’entità del miglioramento di prestazioni. Come è evidente, la modulazione qam offre prestazioni sensibilmente superiori rispetto alla psk.
figure f10.17.png
figure f10.175.png
Esercizio Consideriamo un sistema di modulazione numerica psk con 16 fasi, per il quale si riceva una potenza di segnale Px = 10 − 3 (Volt)2, in presenza di una densità di potenza di rumore PN(f) = 2 ⋅ 10 − 11 (Volt)2/Hz. Si desideri ricevere un flusso numerico a velocità fb = 1 Mbit/sec e si considerino impulsi a coseno rialzato con γ = 0.
Soluzione
  1. Osserviamo che Eb = Px ⋅ Tb = Pxfb = 10 − 3106 = 10 − 9 (Volt)2/Hz, mentre N0 = 2 PN(f) = 4 ⋅ 10 − 11 (Volt)2/Hz, pertanto EbN0 = 25 e ⎛⎝EbN0⎞⎠dB = 10 log10 25 ≃ 14 dB.
    1. Dalle curve delle prestazioni per il PSK si trova che con Eb ⁄ N0 = 14 dB, si ottiene Pe = 10 − 3 qualora si utilizzino 16 livelli.
    2. La banda occupata risulta B = fblog2L = 1064 = 250 KHz.
  2. Le curve delle prestazioni per il qam mostrano che con Eb ⁄ N0 = 14 dB e 16 livelli, si ottiene Pe ≃ 3 ⋅ 10 − 6.
  3. le stesse curve mostrano che, con il 16-qam, la Pe = 10 − 3 si ottiene con Eb ⁄ N0 = 10.5 dB, ovvero 14-10.5=3.5 dB in meno, che corrispondono ad una potenza Px’ = Px100.35 = 10 − 32.24 = 4.47 ⋅ 10 − 5 (Volt)2.
  4. Dimezzare la banda equivale a utilizzare M = 8 bit/simbolo, ovvero raddoppiare log2L, e dunque un numero di livelli L = 2M = 256 = (L’)2. Le curve delle prestazioni per il 256-qam mostrano che per ottenere Pe = 10 − 3 occorre Eb ⁄ N0 ≃ 18.3 dB, pari ad un aumento di 18.3 - 14= 4.3 dB, che equivale ad una potenza Px’ = 100.43 Px ≃ 2.7 ⋅ 10 − 3 (Volt)2.
  5. Ci ritroviamo nelle stesse condizioni del punto 3), con un eccesso di 3.5 dB nel valore di Eb ⁄ N0, che può essere speso riducendo di egual misura Tb, e quindi aumentando fb. Risulta: Tb’ = Tb100.35 e quindi
    fb’ = 1Tb’ = 100.35Tb = 100.35 ⋅ fb = 106.35 ≃ 2.24 Mb/sec.
    E se γ ≠ 0 ? La trattazione del caso di banda base (pag. 1), mostra che l’argomento sotto radice della erfc{} subisce un peggioramento di (1 + γ)⎛⎝1 − γ4⎞⎠, che (per esempio) con γ = 0.5 fornisce 1.31, che deve essere compensato da una uguale diminuzione di Eb ⁄ N0. Nel caso 5), ad esempio, la fb risulterà quindi limitata a fb’’ = fb’ ⁄ 1.31 = 1.71 Mb/sec.
 Sezione 16.2: Modulazione di fase Su Capitolo 16: Modulazione numerica Sezione 16.4: Codifica differenziale