Ci sono almeno due buoni motivi per misurare le grandezze in unità logaritmiche: il primo è che in tal modo si rappresentano in maniera compatta grandezze dalla dinamica molto elevata, ed il secondo è che prodotti e rapporti si trasformano in somme e sottrazioni. Inoltre, c’è almeno un buon motivo psicofisico [422]   [422] Vedi ad es. https://it.wikipedia.org/wiki/Legge_di_Weber-Fechner, basato sulla conoscenza che l’intensità con cui percepiamo gli stimoli attraverso i nostri organi di senso segue naturalmente una legge logaritmica, in quanto per produrre una sensazione che aumenta linearmente, è necessario uno stimolo che aumenta in progressione geometrica. Ciò posto, va anche detto che l’esperienza di insegnamento mostra come, anche se le misure in dB sono qui per aiutarci nei calcoli, esse sono anche uno degli argomenti in cui lo studente medio tende più facilmente a perdersi. Proviamo quindi a fare un po’ di ordine!

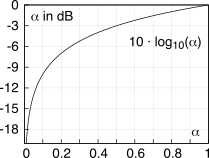
Data una qualsiasi grandezza α, la sua misura in decibel [423]   [423] Dunque un decibel, per come è definito, è la decima parte del Bel, ovvero α_Bel = log₁₀α. Chissà, forse dopo che definirono il Bel, si accorsero che era troppo grande ? :-) è definita come e descrive le relazioni mostrate nella figura 8.2, a sinistra per valori α > 1, ed a destra per α < 1, a cui corrispondono rispettivamente valori in decibel positivi e negativi. Inoltre, sempre in fig. 8.2 è mostrata una tabella con alcune corrispondenze che possono comunemente ricorrere: ad esempio, dato che log₁₀2 = 0.30102..., un valore α pari a 2 equivale a circa 3 dB.

Nota una grandezza espressa in dB, si può risalire al suo valore naturale mediante l’ovvia relazione inversa

Per esprimere un rapporto R = α β molto grande o molto piccolo, si ricorre spesso alla scala logaritmica definita dai dB, calcolando direttamente il rapporto in tali termini, ovvero eseguendo la differenza tra le grandezze α e β espresse in dB, in quanto Se le due grandezze α e β sono omogenee, come ad esempio due potenze di segnale P_x e P_y espresse in V², o due potenze W_x e W_y espresse in Watt, allora il loro rapporto è un numero puro, e la sua misura in dB esprime di quanti dB il numeratore è maggiore (o minore) del denominatore. Conoscendo una delle due grandezze, ed il valore del loro rapporto, si può ovviamente risalire al valore dell’altra, ovvero ad esempio ma, perché questa ovvia relazione possa avere una utilità pratica, occorre sapere cosa rappresenta β, dopodiché potremo concludere che α rappresenta la stessa cosa [424]   [424]  Ad esempio volt², oppure watt., ma R_dB decibel più grande. Per questo, si definisce la

La (10.200) può essere usata per esprimere il valore assoluto di una grandezza, assieme alla sua unità di misura, se viene pensata come una applicazione della (10.201), ponendo il denominatore pari all’unità di misura stessa. Così ad esempio una potenza W_x di α Watt ( [425]   [425] Al cap. 18 verrà approfondita la differenza tra potenza di segnale, espressa in volt² o ampere², e potenza assorbita, dissipata o trasmessa, espressa in watt.) viene espressa come ovvero, misurandola in dB sopra il Watt. Quindi, una potenza misurata in dBW può ricondursi alla corrispondente potenza in Watt, calcolando ed allo stesso modo si può finalmente applicare la (10.202) per ottenere una grandezza effettiva:

Se invece che in Watt il valore β risulta espresso in milliWatt (1 mW = 10^− 3 Watt) la corrispondente misura logaritmica viene indicata come dBm (dB riferiti al mWatt), valutato come β_dBm = 10 ⋅ log₁₀β_mWatt. Pertanto, essendo β_mW = 10³ ⋅ β_W, possiamo scrivere e dunque per passare da una unità di misura ad un’altra, esprimendo le stesse in dB, occorre sommare (o sottrarre) il relativo fattore di scala, anch’esso espresso in dB.

Qualora la grandezza da esprimere in unità logaritmiche non sia la potenza totale di un segnale, bensì la relativa densità di potenza espressa in V² Hz o W Hz (a seconda se si tratti di potenza di segnale o fisica), ovvero dai multipli e sottomultipli dando luogo a densità di potenza espresse in mW Hz o W MHz o mW MHz, è ancora possibile applicare la (10.200) purché intesa nel senso della (10.203), ossia indicando l’unità di misura di partenza, individuando così valori di densità di potenza espressi in termini assoluti come dBV² Hz, dBW Hz, dBW MHz, dBm MHz....

Tali unità di misura torneranno utili in sede di valutazione del bilancio di collegamento, affrontato al cap. 19.