Qualora la portante di demodulazione presenti una ambiguità di fase residua si può applicare la tecnica della codifica differenziale esposta al § 16.4, oppure inserire una sequenza di simboli noti (o flag) all’inizio della trama trasmissiva, in modo che il confronto tra i valori previsti e quelli ricevuti permetta di correggere tale ambiguità. Da notare che i flag o trailer ad inizio trama possono essere vantaggiosamente usati anche da schemi di recupero del clock del tipo di quelli al § 15.7.2.1.

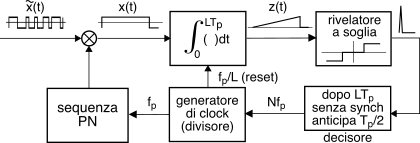
Considerando già avvenuta la sincronizzazione di portante e la demodulazione, il primo passo può essere attuato mediante lo schema in figura detto sliding correlator, in cui l’integratore (ad es. un integrate and dump) calcola la correlazione tra la pn in arrivo e quella generata localmente. In caso di coincidenza temporale il risultato z(t) è una rampa (negativa se il bit fosse stato  − 1), mentre per un ritardo θ tra la seq. locale e quella ricevuta il risultato dell’integrazione all’istante LT_p è l’autocorrelazione R_x̃(θ), più termini di rumore a valor atteso nullo. Alla conclusione del periodo di bit T_b = LT_p il generatore di clock resetta l’integratore, non prima però che il rivelatore a soglia abbia prodotto un impulso di sincronismo, inibendo il componente di decisione e terminando la ricerca. In assenza di sincronizzazione, il decisore fa invece avanzare la fase della pn di ^T_p⁄₂, tentando di nuovo l’aggancio. Il metodo richiede dunque 2L²T_p secondi (nel caso peggiore), tempo che può essere ridotto eseguendo più ricerche in parallelo.

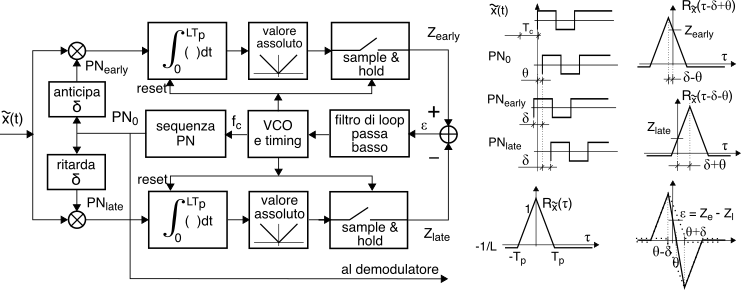
Dopo aver acquisto la sincronizzazione lasca il controllo della generazione della pn passa ad un circuito indicato come delay locked loop o dll, che può essere realizzato in diversi modi, e di cui discutiamo il funzionamento dello schema canonico mostrato in fig. 16.64.Un generatore pseudonoise produce la sequenza pn₀ affetta dall’errore di temporizzazione residuo  − ^T_p⁄₂ ≤ |θ| ≤ ^T_p⁄₂, che ai fini della discussione assumiamo come un ritardo, e dunque scriviamo pn₀ = x̃(t − θ); lo scopo del dll è di rendere θ = 0. Da pn₀ sono derivate due nuove sequenze, pn_early = x̃(t − θ + δ) e pn_late = x̃(t − θ − δ), che differiscono da pn₀ rispettivamente per un anticipo od un ritardo δ < ^T_p⁄₂, e che sono moltiplicate per il segnale allargato di banda base x̃(t). L’integratore del ramo superiore (early) calcola pertanto l’autocorrelazione [912]   [912] L’esempio si riferisce ad una sequenza pn di massima lunghezza, della cui autocorrelazione si è discusso a pag. 1.    tra x̃(t) e la sua copia in anticipo di δ − θ, mentre quello inferiore (late) calcola R_x̃(− δ − θ) tra x̃(t) e la sua copia in ritardo di δ + θ (vedi lato destro di fig. 16.64): questi due risultati sono campionati [913]   [913] Il blocco che valuta il valore assoluto dell’uscita dell’integratore è necessario in quanto x̃(t) trasporta anche l’informazione x(t), che determina l’eventuale inversione di segno della sequenza pn, e dunque un cambiamento di segno per l’uscita dell’integratore. a fine sequenza, ed indicati con z_early e z_late; notiamo che se θ = 0, si ha z_early = z_late = R_x̃(δ).

Proseguendo con l’esempio, osserviamo come l’evenienza z_early > z_late indichi che la fase di pn_early è più prossima a quella del segnale ricevuto di quanto non lo sia quella di pn_late, e dunque pn₀ è in ritardo, ovvero stiamo andando... troppo piano [914]   [914] In altri termini, le tre copie della pn (₀, _early e _late) dovrebbero slittare a sinistra, e quindi il periodo della pn deve essere ridotto.. In questo caso la differenza ε = z_early − z_late risulta positiva (vedi costruzione grafica in basso a ds in fig. 16.64), e ciò determina (attraverso il filtro di loop) una accelerazione del vco, che tende quindi a ridurre il ritardo iniziale θ. Se si fosse verificato l’opposto (θ < 0 e dunque z_early < z_late) sarebbe risultato ε < 0, a cui corrisponde un rallentamento del vco.

Man mano che θ si riduce, pn_early e pn_late tendono a disporsi simmetricamente in anticipo ed in ritardo di δ rispetto a pn₀, in modo che z_early e z_late prendono il medesimo valore e la loro differenza ε si annulla, la f_c prodotta dal vco è costante, e pn₀ è esattamente in fase con x̃(t). Mentre θ si azzera, la costruzione grafica in basso a destra di fig. 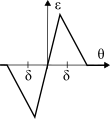16.64 transla verso sinistra, in modo che corrisponda ε = 0 per θ = 0. Ciò consente di riformulare l’approccio grafico come nella figura a lato, che rappresenta l’errore ε in funzione del disallineamento θ, detta anche curva di discriminazione o curva-s, e che evidenzia l’intervallo |θ| < δ entro il quale il sistema converge. Questa figura è simile a quella discussa al § 12.2.2.2 a proposito del pll, ed infatti l’analisi delle prestazioni ha molto in comune. In particolare una diminuzione della banda del filtro di loop, se da un lato riduce le capacità di inseguire rapide variazioni di ritardo (come potrebbe essere per effetto doppler), d’altro canto attenua l’influenza del rumore sulla varianza della stima di θ.