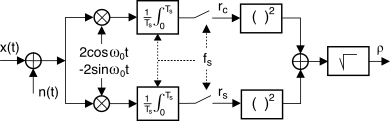
In realtà è ancora praticabile la tecnica ook (on off keying), ovvero una modulazione pam della portante con un impulso nrz polare, oltre a quella dell’fsk incoerente. Per entrambe si tratta di rivelare la presenza/assenza di una sinusoide nel rumore, per la durata di un bit T_b o di un simbolo T_s, e si ricorre allo schema di demodulazione discusso al § 12.2.4 e riportato a fianco, in cui la portante di demodulazione è una di quelle dell’fsk, oppure l’unica nel caso di ook, ed il generico passa basso è realizzato come un integratore, ovvero con risposta impulsiva [855]   [855] Ad esempio realizzato mediante un integrate and dump (pag. 1), che deve essere resettato a fine T_s. h(t) = 1T_s rect _Ts(t), ovvero ancora come un filtro adattato all’impulso di trasmissione g(t) = rect_Ts(t) [856]   [856] Il fattore ¹⁄_Ts che compare nell’espressione di h(t) rende l’energia dell’impulso complessivo g(t) * h(t) = tri_2Ts(t) (vedi eq. (10.56)) normalizzata rispetto a T_s (vedi § 3.8.8)., in modo da scrivere il segnale ricevuto come in cui a_k = A se la frequenza f₀ è attiva durante il simbolo k, oppure a_k = 0 nel caso opposto. Il rumore n(t) in ingresso, con densità di potenza N₀2, rende le grandezze di osservazione r_c e r_s due v.a., che nel caso di segnale presente hanno valor medio [857]   [857] Infatti il segnale demodulato (as es.) sul ramo in fase ha ampiezza costante A1T_scosθ, che risulta moltiplicata per T_s quando integrato su tale periodo. m_c = Acosθ e m_s = Asinθ, oppure zero per segnale assente, mentre in entrambi i casi e per entrambi i rami la varianza risulta pari a [858]   [858]  Infatti il filtro adattato ha una |G(f)|² = sinc²(T_sf), e dunque il rumore alla sua uscita (vedi § 14.1.3 e pag. 1) presenta una densità di potenza P_n(f) = N₀sinc²(T_sf). La potenza di rumore perciò risulta pari a P_n = σ² = N₀T_s, in quanto n(t) è a media nulla, e ∫^∞_−∞sinc²(T_sf) = 1T_s. Quest’ultimo risultato può essere verificato considerando che sinc²(T_sf) ha antitrasformata 1T_s tri _2Ts(t), e che per la proprietà del valore iniziale (pag. 1) ∫^∞_−∞sinc²(T_sf) = 1T_s tri _2Ts(t = 0) = 1T_s. σ² = ^N₀⁄_Ts.

La decisione se sia presente o meno la frequenza è basata sul modulo dell’inviluppo complesso r = r_c + jr_s, ovvero ρ = √r²_c + r²_s, ed attuata mediante l’approccio di massima verosimiglianza esposto al § 14.4.2. Nelle ipotesi poste, il caso in cui a_k = 0 corrisponde ad osservare una v.a. di Rayleigh (pag. 1) con d.d.p. mentre se a_k = A si osserva [859]   [859] La discussione a pag. 1 fa riferimento ad una sola v.a. (quella in fase) a media A, mentre nel caso attuale sia ha ρ = A ma con una fase qualsiasi. Per le proprietà di simmetria radiale del problema, la conclusione è valida anche nel nostro caso. una v.a. di Rice, con d.d.p. ed in questa circostanza si è trovato (eq. 14.108) che se le due ipotesi di segnale presente (H₁) ed assente (H₀) sono equiprobabili e la soglia di decisione è posta pari a ^A⁄₂, la probabilità di errore può essere approssimata come P_e = 12  e^− A28σ2.

Nel caso dell’ook osserviamo che ^A2⁄₂ è la potenza di una sinusoide di ampiezza A, ma se questa per metà del tempo (gli a_k = 0) è spenta la potenza si dimezza, e così risulta E_b = P_sT_b = A²4 T_b; sostituendo dunque A²4 = ^E_b⁄_Tb e σ² = ^N₀⁄_Tb nell’espressione della P_e otteniamo

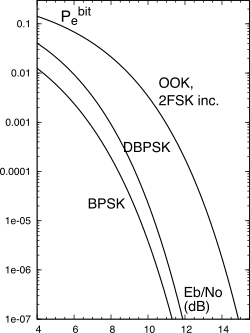
La stessa espressione descrive anche le prestazioni per una modulazione fsk a due livelli: in tal caso infatti la decisione avviene confrontando due v.a. ρ₁, ρ₂ con distribuzione una di Rice e l’altra di Rayleigh, ottenute duplicando lo schema di fig. 16.33 per le due frequenze (ortogonali) utilizzate, associate ad uno stesso bit uno o zero, e dunque il problema statistico è identico al precedente. La figura 16.34 permette il confronto delle prestazioni tra le tecniche di modulazione binarie presentate.