Capitolo 16: Modulazione numerica Su Capitolo 16: Modulazione numerica Sezione 16.2: Modulazione di fase 

16.1 Modulazione di ampiezza

In questo caso l’informazione numerica è impressa sulla portante alterando le ampiezze di una (o entrambe, come mostrato al § 16.3) delle componenti analogiche di bassa frequenza.

16.1.1 Modulazione BPSK

E’ l’acronimo di Bi-Phase Shift Keying [815]   [815] Letteralmente, slittamento di tasto a due fasi., e individua una tecnica per il trasporto dell’informazione basata sull’utilizzo di 2 possibili fasi per la portante:
(21.33) xBPSK(t) = asin(ω0t + φ(t))       dove      φ(t) = ∞⎲⎳k = −∞φk rectTb(t − kTb)
con i valori φk pari a ± π2 per rappresentare le cifre binarie 0 ed 1 trasmesse agli istanti kTb. Sebbene l’operazione così definita corrisponda ad una modulazione di fase (§ 12.3), è facile mostrare come possa essere realizzata mediante una comune modulazione di ampiezza bld-ps (§ 12.1.1) con segnalazione antipodale (§ 7.6.1). Se definiamo infatti un segnale m(t) come un codice di linea nrz bipolare (§ 15.2.1), che assume valori ±1 in corrispondenza delle cifre binarie 0 ed 1, allora il segnale
xBPSK(t) = m(t) cosω0t
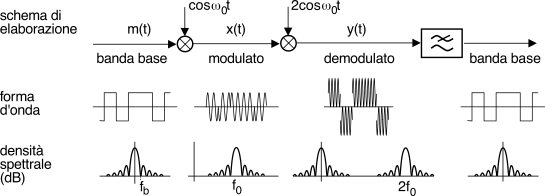
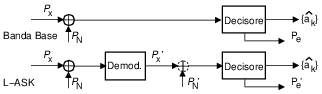
è equivalente a quelle espresso dalla (21.33), e la sua mo-demodulazione coerente avviene mediante l’architettura mostrata alla fig. 16.1. Il segnale uscente dal moltiplicatore di demodulazione [816]   [816] Qui e nel seguito assumiamo di disporre di una portante di demodulazione omodina o coerente (§ 12.2.1), ossia priva di errori di fase e frequenza, così come di una perfetta temporizzazione di simbolo; le considerazioni al riguardo di quest’ultimo aspetto sono svolte all’appendice 16.11. ha espressione
y(t) = x(t) ⋅ 2cosω0t = 2m(t) ⋅ cos2ω0t = m(t) + m(t) ⋅ cos2ω0t
e dunque il codice di linea m(t) può essere riottenuto mediante filtraggio passa-basso. La parte centrale di fig. 16.1 mostra la forma d’onda che corrisponde alle elaborazioni previste, mentre nella parte inferiore sono raffigurate le densità spettrali corrispondenti (espresse in dB, vedi § 8.1), tenendo conto [817]   [817] Il segnale di banda base m(t) = ∑kak ⋅ g(t − kTb) in cui g(t) =  rectTb(t) ed i simboli ak sono a media nulla ed indipendenti, ha una densità di potenza Pm(f) = σ2ATbsinc2(fTb), il cui andamento è mostrato in fig. 3.18 di pag. 1. di eq. (21.2), di fig. 3.18, e della mo-demodulazione bld-ps (§ 12.1.1.1).
figure f10.1.png
Figure 16.1 Architettura di mo-demodulazione bpsk, forma d’onda, e densità spettrale
Una buona caratteristica di questa tecnica è il valore costante dell’ampiezza della portante modulata, che permette di utilizzare la massima potenza al trasmettitore, appena inferiore al valore che inizia a produrre fenomeni di distorsione (§ 13.3). L’aspetto negativo è l’elevata occupazione di banda, legata all’uso di forme d’onda rettangolari per m(t) che, nel caso di trasmissione su canali con limitazioni di banda, causa vincoli sulla massima frequenza binaria. Pertanto il metodo è particolarmente indicato nel caso di collegamenti in cui è limitata la potenza di trasmissione, ma non la banda [818]   [818] Come ad esempio i collegamenti satellitari, vedi § 25.3..
Alternative per l’impulso di banda base g(t)
Riprendendo i concetti discussi al § 15.2, in questo capitolo il segnale dati di banda base (ovvero pre-modulazione) è realizzato mediante una delle seguenti possibilità di scelta per l’impulso g(t):
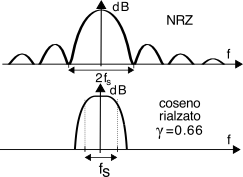
figure f10.8b.png
Gli aspetti prima evidenziati per il bpsk sono sovvertiti qualora il segnale m(t) sia basato su forme d’onda g(t) con una limitata occupazione di banda, come per il coseno rialzato, con una banda a frequenze positive pari a BBPSK = fb(1 + γ), doppia rispetto al caso di banda base, a causa della modulazione bld, mentre l’ampiezza del segnale modulato non è più costante. Infatti in corrispondenza degli istanti kTb l’ampiezza di xBPSK(t) assume esattamente uno dei valori (±1) del segnale dati m(t), ma nell’intervallo tra due istanti kTb < t < (k + 1)Tb l’ampiezza dipende della somma di tutte le code delle funzioni g(t) relative ai simboli trasmessi (vedi fig. 15.23 a pag. 1).

16.1.2 Modulazione L-ASK

Ci riferiamo ora al caso in cui si operi una classica am-bld (da cui il termine Amplitude Shift Keying - ask) a partire da un segnale dati m(t) multilivello (§ 15.1.2.4), producendo un segnale modulato di espressione
xL−ASK(t) = m(t) cos(2πf0t)     dove    m(t) = ∑∞k = −∞ ak ⋅ rectTs(t − kTs)
figure f10.1a.png
in cui m(t) agli istanti kTs assume valori ak distribuiti uniformemente, in un intervallo Δ, su L livelli di ampiezza centrati sullo zero [819]   [819] Per chi si sta chiedendo quanto valgono questi livelli, diciamo che il livello i-esimo (con i = 0, 1, ⋯, L − 1) corrisponde al valore ai = i ⋅ ΔL − 1 − 1 . Verificare per esercizio con Δ = 2 ed L = 4.. L’ampiezza di l-ask subisce dunque variazioni, come mostrato nella figura soprastante per un caso con L = 8, in cui è rappresentato anche un diagramma detto costellazione, che rappresenta i valori assunti dall’inviluppo complesso in corrispondenza degli istanti di simbolo, che in virtù della am-bld presenta la sola c.a. di b.f. xc(t).
figure f10.1b.png
Figure 16.4 Densità spettrale di l-ask
in diverse unità di misura
Ogni ak rappresenta dunque M = log2L bit, ed il periodo di simbolo Ts = MTb ha durata multipla di Tb, pertanto la banda occupata da l-ask è minore rispetto a quella del bpsk di un fattore pari a M = log2L( [820]   [820] Ad esempio: se L = 32 livelli, la banda si riduce di 5 volte, ed infatti con M = 5 bit si individuano L = 2M = 32 configurazioni. Dato che il numero M di bit/simbolo deve risultare un intero, si ottiene che i valori validi di L sono le potenze di 2.). 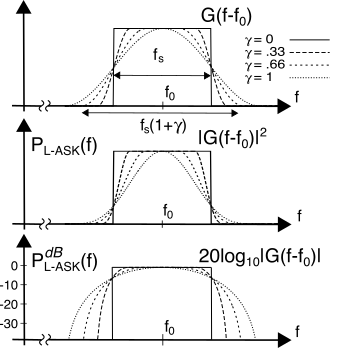Anche in questo caso, se m(t) è generato mediante un impulso a coseno rialzato anziché con uno nrz [821]   [821] Notiamo che mentre per il bpsk scegliere il primo al posto del secondo comporta perdere i benefici di una ampiezza costante, nel caso multilivello l’ampiezza è intrinsecamente variabile., la densità spettrale assume il noto andamento (vedi pag. 1) riportato ora in figura 16.4, assieme ai corrispettivi valori in dB. Pertanto la banda a frequenze positive occupata da xL − ASK(t) con g(t) a coseno rialzato vale
(21.34)
BL − ASK = fs(1 + γ) = fblog2L(1 + γ)
Efficienza spettrale o densità di informazione
E’ definita come il rapporto ρ tra la frequenza binaria e la banda occupata
(21.35) ρ = fbB
e si esprime in bit/sec/Hz, rappresentando appunto quanti bit/sec sono trasmessi per ogni Hz utilizzato. Nel caso di l-ask con impulsi a banda minima (γ = 0) si trova allora
(21.36) ρL − ASK = fbB = log2L
mentre per altre forme di modulazione e/o di impulsi si ottengono altri valori [822]   [822] Vedi tabella 16.2 a pag. 1., confrontando i quali si valuta la bontà di un metodo rispetto all’altro nei termini dell’utilizzo di banda.
Esempio Se compariamo il risultato per ρL − ASK con quello relativo ad una trasmissione numerica di banda base (vedi eq. (21.5)), notiamo un peggioramento di un fattore 2, dovuto all’uso di una am-bld.
Come per il caso analogico, la banda potrebbe essere dimezzata adottando una am-blu, ma troveremo invece tra breve che si preferisce seguire approcci diversi, come ad esempio psk e qam.

16.1.3 Valutazione delle prestazioni

Dopo alcune considerazioni relative al legame tra SNR ed occupazione di banda, la valutazione della Pe fa tesoro di quanto ottenuto al § 15.4.
SNR, Eb ⁄ N0 ed efficienza spettrale
Nell’analisi delle prestazioni che affronteremo la probabilità di errore per simbolo Pe(simbolo) o per bit Pe(bit) è espressa in funzione della grandezza EbN0 introdotta a pag. 1, e che rappresenta l’equivalente del rapporto segnale rumore di sistema SNR0 =  PxN0W definito al § 14.2.1.1 [823]   [823] Ricordiamo che Px esprime la potenza ricevuta, N0 rappresenta il doppio della Pn(f) presente al decisore, e W è la banda del segnale modulante., nel senso che come questo consente il confronto tra tecniche diverse [824]   [824] Infatti come discusso a pag. 1 Eb = Pxfb, come N0, dipende solamente da parametri di sistema (Px e fb), mentre invece non dipende dai parametri di trasmissione L e γ e dal tipo di modulazione.. D’altra parte, una trasmissione am-bld numerica che occupi una banda a frequenze positive B si presenta in ingresso al decisore con un
(21.37)
SNR = PxPn = Ebfb2B ⋅ N0⁄2 = EbN0 fbB = ρ EbN0
in cui Pn è limitata da un filtro di ricezione, e ρ è l’efficienza spettrale definita alla (21.35): pertanto Eb⁄N0 è anche indicato come SNR normalizzato o SNR per bit. Nel caso di g(t) a banda minima (§ 15.2.2.3) la (21.36) fornisce ρL − ASK = log2L e dunque SNR = log2L EbN0, mentre a pag. 1, eq. (21.16), si deriva la relazione tra Eb⁄N0 e SNR per il caso particolare di un segnale dati a coseno rialzato.
Invertendo la (21.37) si ottiene Eb⁄N0 = SNR⁄ρ evidenziando come, a parità di SNR,  al miglioramento dell’efficienza spettrale ρ corrisponda una diminuzione di EbN0, che a sua volta è causa di un peggioramento della probabilità di errore, in accordo con il compromesso banda-potenza, vedi § 15.4.7.
Probabilità di errore BPSK e L-ASK
La Pe viene calcolata per un segnale l-ask in funzione di Eb ⁄ N0, al variare del numero di livelli, ottenendo il caso bpsk per L = 2.
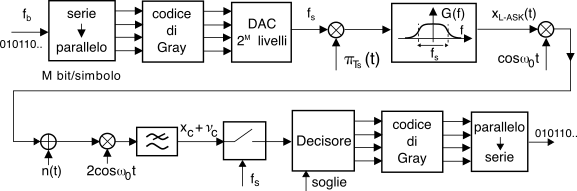
Al § 16.1.2 abbiamo osservato come l’l-ask sia ottenibile mediante una modulazione am-bld di un segnale dati di banda base (vedi anche fig. 16.5), e come discusso al § 14.2.1.1, l’SNR in uscita dal filtro di ricezione (e dunque l’Eb⁄N0, vedi eq. (21.37)) per una modulazione am-bld è pari al rapporto SNR0 tra potenza ricevuta e potenza di rumore nella banda del segnale modulante.
figure f10.5a.png
Figure 16.5 Schema di mo-demodulazione per un segnale l-ask
Pertanto l’SNR (e l’Eb⁄N0) dopo demodulazione di l-ask è pari a quello che si avrebbe per il segnale dati di banda base da cui ha origine. Le prestazioni per un segnale dati di banda base a coseno rialzato sono ricavate al §  15.4.9, che riportiamo sotto come probabilità di errore per simbolo dell’l-ask [825]   [825]  Forniamo qui una contro-dimostrazione forse inutilmente elaborata. Con riferimento alla figura seguente, il calcolo della Pe per l’l-ask si imposta definendo valori di Eb ed N0 equivalenti a quelli di banda base, ma ottenuti dopo demodulazione, e cioè Eb’ = Px’Tb e N0’ = PN’ ⁄ W (infatti, PN’ = N0’22W, con W = fs2 = fb2log2L). L’equivalenza è presto fatta, una volta tarato il demodulatore in modo che produca in uscita la componente in fase xc(t) limitata in banda tra ± W.
figure f10.6.png
Infatti in tal caso (vedi § 14.2.1) Px’ = Pxc = k2aPM = 2Px e quindi Eb’ = Px’Ts = 2PxTs = 2Eb; per il rumore si ottiene N0’ = PN’W in cui PN’ = Pnc = σ2nc = σ2n = N024W e quindi N0’ = 2N0. Pertanto, il valore Eb’ ⁄ N0’ su cui si basa ora il decisore è lo stesso Eb ⁄ N0 in ingresso al demodulatore.
(21.39)
PL−ASKe(simbolo) = ⎛⎝1 − 1L⎞⎠ erfc⎧⎨⎩√3 EbN0 log2L(L2 − 1)⎫⎬⎭
valida per un segnale con γ = 0, ossia a banda minima [826]   [826] Se γ ≠ 0, valgono le considerazioni svolte al § 15.4.9.. Le curve di PL − ASKe(bit) in funzione di Eb⁄N0|dB sono quelle di fig. 15.39 a pag. 1, dove si tiene anche conto dell’uso di un codice di Gray (§ 15.4.9.1) per associare i livelli a configurazioni binarie.
 
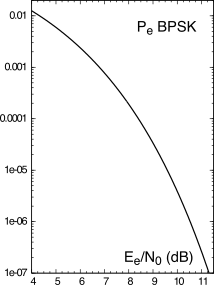
figure f-ber-bpsk.png
Figure 16.6 Prestazioni bpsk
Come anticipato, per L = 2 la (21.39) esprime le prestazioni del bpsk, ovvero
(21.40) PBPSKe(bit) = 12 erfc⎧⎨⎩√EbN0⎫⎬⎭
che come prima si riferisce al caso di banda minima, ed i cui valori sono graficati in fig. 16.6, identica alla (21.18) ottenuta per il caso di banda base, ed alla (10.176) relativa al filtro adattato. Per completare i confronti osserviamo che ora all’aumentare di L la banda (21.34) (per γ = 0)
BL − ASK = fs = fblog2L
si riduce, mentre la Pe (21.39) aumenta: ciò può tornare utile in presenza di canali con limitazioni di banda ma non di potenza, dato che in tal caso la Pe può essere ripristinata aumentando la potenza e quindi Eb⁄N0, in base al cosiddetto compromesso banda-potenza. Al § 16.5.1 vedremo come nella tecnica di fsk ortogonale lo stesso compromesso operi in direzione opposta, ovvero riuscendo a migliorare Pe al prezzo di aumentare l’occupazione di banda.
 Capitolo 16: Modulazione numerica Su Capitolo 16: Modulazione numerica Sezione 16.2: Modulazione di fase