16.5 Modulazione di frequenza L-FSK
Qualora si desideri che l’ampiezza del segnale modulato si mantenga strettamente costante si può adottare la tecnica di modulazione
fsk (
Frequency Shift Keying), che associa ad ogni simbolo
ak ottenuto raggruppando
M bit, uno tra
2M = L possibili valori (o
livelli) di frequenza
fk, da sommare a quello della portante in accordo all’espressione
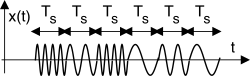
xFSK(t) = cos [2π(f0 + m(t))t] dove m(t) = Δ ⋅ ∞⎲⎳k = −∞fk ⋅ rectTs(t − kTs)
in cui ogni elemento della sequenza
fk assume uno tra gli
L valori
{0, 1, 2, …, L − 1}. Si tratta in altri termini di una portante la cui frequenza nominale
f0 è
alterata di una quantità
Δ ⋅ fk Hz per un intervallo temporale pari al periodo di simbolo
Ts, in cui
Δ rappresenta ora la spaziatura (uniforme) tra le frequenze associate agli
L livelli. Pertanto l’espressione può essere riscritta come
Il risultato è senza dubbio ad ampiezza costante; se
Ts ≫ 1f0 si può adottare uno schema di mo-demodulazione basato su di un
vco ed un
pll (vedi §
12.2.2.2 e
12.3.2.1) riportato (per
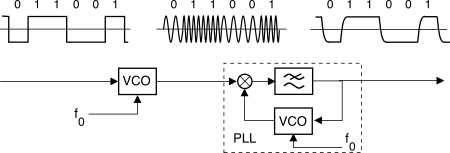
L = 2) in figura
16.29, in cui all’uscita del passa basso ritroviamo il segnale modulante.
Lo schema è effettivamente utilizzato per modem a bassa velocità e basso costo, ed ha il pregio di funzionare anche in presenza di errori tra l’f0 usata dal vco del trasmettitore e quella del ricevitore. Per raggiungere velocità fb più elevate a parità di L, occorre ridurre Ts, in modo da aumentare fs = 1Ts e quindi fb = fsM = fs log2L. In tal caso può essere necessario ricorrere ad un demodulatore più complesso, come descritto appresso.
16.5.1 Modulazione FSK ortogonale
Nel caso in cui si realizzi la condizione
Δ = l⁄2Ts con
l intero, le diverse frequenze
f0 + Δfk sono
ortogonali, e può essere adottato un
demodulatore a correlazione (vedi §
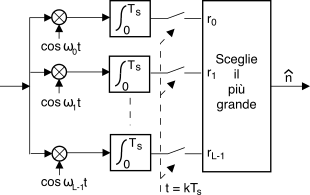
7.6.2), realizzato mediante un banco di correlatori
ed una decisione di massimo (fig.
16.30), in cui l’
n − esimo correlatore esegue
dove
f0 + mΔ rappresenta la frequenza (incognita) in arrivo, mentre
f0 + nΔ è una delle frequenze possibili, con
n ∈ {0, 1, 2, …, L − 1}. Essendo tali frequenze tra loro
ortogonali entro l’intervallo di integrazione, al termine del calcolo una sola delle uscite sarà diversa da zero. Come discusso al §
7.6 in presenza di rumore l’uscita di ogni correlatore diviene una v.a. con varianza
N02 EG,
corrompendo l’ortogonalità tra simboli, e dunque si rende necessaria l’operazione di confronto per realizzare una decisione di
massima verosimiglianza (§
6.6.2.1). Indicando infatti con
rn, n = 0, 1⋯, L − 1 la grandezza prodotta dal campionatore
n − esimo, e con
r = [r0, r1, ⋯rL − 1] il vettore aleatorio
L − dimensionale corrispondente, la scelta del maggiore tra gli
rn corrisponde a scegliere l’ipotesi
fn̂ che rende massima la
p(r ⁄ fn̂).
In generale, se ogni diversa
fk è equiprobabile l’
fsk ha una densità spettrale del tipo mostrato alla figura
16.31.
Se
L≫1, l’occupazione di banda complessiva risulta quindi (circa) uguale a
L ⋅ Δ. Nel caso di
modulazione coerente (vedi nota
846) la minima spaziatura è di
Δ = 12Ts = fs2, e dunque nel caso di
L elevato la minima banda occupata può essere approssimata come
mentre per quanto riguarda l’efficienza spettrale si ottiene
ρFSK = fbB = fb ⋅ 2fb ⋅ log2LL = 2L log2 L
ossia
L2 volte
peggiore dell’
l-ask (pag.
1). Ma: se l’efficienza spettrale è così bassa, che vantaggi ci sono ad usare l’
fsk? ... a sua
difesa, portiamo i seguenti argomenti:
Il caso
semplice con
Ts ≫ 1f0
può essere demodulato con lo schema a
pll rappresentato in fig.
16.29, di facile realizzazione ed economico: ad esempio, veniva usato per salvare su
compact cassette audio i dati degli
home computer degli anni ’70
l’efficienza spettrale è quasi ρBFSK = 2L log2L||L = 2 = 1, come per il caso del bpsk. Al contrario, al crescere di L l’efficienza spettrale diviene sempre peggiore.
Si può dimostrare che l’uso dello schema di fig.
16.30 e di portanti di demodulazione ortogonali e coerenti permette di ottenere una
che deve essere valutata per via numerica, e che può essere resa
piccola a piacere, nei limiti previsti dalla teoria dell’informazione, semplicemente aumentando
L (e dunque
Ts).
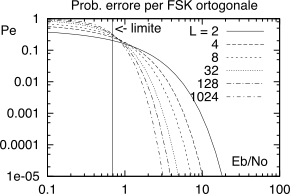
La figura a lato mostra i valori della
(21.55) in funzione di
Eb ⁄ N0 per diversi valori di
L, e illustra come all’aumentare di quest’ultimo sia necessaria sempre minor potenza per ottenere la stessa
Pe, a patto che risulti
Eb ⁄ N0 > ln 2 = 0, 69
che rappresenta il valore noto come
limite di Shannon-Hartley,
ricavato a pag.
1.
Il miglioramento di
Pe con
L è una manifestazione del
compromesso banda-potenza: osserviamo infatti che anche la banda occupata
BFSK ≃ fb2 Llog2 L aumenta (a parità di
fb) all’aumentare di
L, e dunque a parità di
Eb ⁄ N0 l’
fsk riesce ad ottenere
Pe arbitrariamente piccole, a spese di una occupazione di banda sempre maggiore. L’aumento di
L però non può essere illimitato, sia per le limitazioni di banda del canale, che a causa della complessità del ricevitore, a cui si aggiunge il ritardo temporale necessario ad accumulare gli
M = log2L bit che realizzano un simbolo con un enorme numero
L di livelli.
Discussione sull’ottimalità per
L → ∞
Osserviamo innanzitutto che il ricevitore a correlazione commette errore quando il rumore sovrapposto al segnale di ingresso è casualmente “simile” ad una delle cosinusoidi utilizzate per la trasmissione. In tal caso, l’uscita dell’integratore relativo alla frequenza “simile” può superare quella relativa alla frequenza trasmessa, e corrotta dal medesimo rumore. All’aumentare di
L (per
fb fisso) aumenta il periodo di simbolo
Ts = log2 Lfb e quindi diventa sempre più “difficile” per il rumore emulare “bene” una della frequenze di segnalazione, e quindi si riduce la probabilità di errore. La nota
934 a pag.
1 propone una interpretazione analitica di questo fenomeno.
Chiaramente, all’aumentare di L aumenta proporzionalmente la complessità del ricevitore, che deve disporre di un numero di correlatori crescente. Pertanto, le prestazioni ideali per L che tende ad infinito rivestono solamente un interesse teorico.